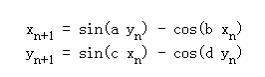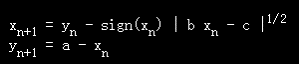【分形简介】
分形,具有以非整数维形式充填空间的形态特征。分形(Fractal)一词,是芒德勃罗创造出来的,其原意具有不规则、支离破碎等意义。1973年,芒德勃罗(B.B.Mandelbrot)在法兰西学院讲课时,首次提出了分维和分形的设想。
分形是一个数学术语,也是一套以分形特征为研究主题的数学理论。分形理论既是非线性科学的前沿和重要分支,又是一门新兴的横断学科,是研究一类现象特征的新的数学分科,相对于其几何形态,它与微分方程与动力系统理论的联系更为显著。分形的自相似特征可以是统计自相似,构成分形也不限于几何形式,时间过程也可以,故而与鞅论关系密切。
分形几何是一门以不规则几何形态为研究对象的几何学。由于不规则现象在自然界普遍存在,因此分形几何学又被称为描述大自然的几何学。分形几何学建立以后,很快就引起了各个学科领域的关注。不仅在理论上,而且在实用上分形几何都具有重要价值。
分形现已成为应用极为广泛的学科。芒德布罗个人风格独特,对各类看似“无定形”、“不光滑”的“怪东西”皆富有兴趣,也正是这样他才能最终抽象创立出分形这门学科。曼德布罗特来访过中国大陆一次以上,称中国文字个个是图形,与他路数相合(芒德布罗本人习用法语)。中国最早使用分形理论的可能是金属学界。
【著名的分形实例】
现今人们熟悉的分形的著名实例,如用“镂空”办法制成的康托尔集、谢尔宾斯基三角形(Waclaw Sierpinski,1882-1969,波兰数学家)及门格奶酪或称门格海绵(Menger,1902-1985,为著名经济学家门格之子),它们的非整数维数是渐增的,分别为0.63、1.58、2.72,而它们长度、面积、体积令人吃惊的皆为0。另一个用“凸起”办法制作的科赫曲线(H.von Koch,1870-1924,瑞典数学家),其维数是1.26,它的长度则是无限的,可它围住的面积却有限!
生活中,我们平常吃的西兰花也是很典型的分形实例。我们可以看到西兰花一小簇是整个花簇的一个分支,而在不同尺度下它们具有自相似的外形。换句话说,较小的分支通过放大适当的比例后可以得到一个与整体几乎完全一致的花簇。因此我们可以说西兰花簇是一个分形的实例。
【分形的由来】
据芒德布罗教授自己说,fractal一词是1975年夏天的一个寂静夜晚,他在冥思苦想之余偶翻他儿子的拉丁文字典时,突然想到的。此词源于拉丁文形容词fractus,对应的拉丁文动词是frangere(“破碎”、“产生无规碎片”)。此外与英文的fraction(“碎片”、“分数”)及fragment(“碎片”)具有相同的词根。在70年代中期以前,芒德布罗一直使用英文fractional一词来表示他的分形思想。因此,取拉丁词之头,撷英文之尾的fractal,本意是不规则的、破碎的、分数的。芒德布罗是想用此词来描述自然界中传统欧几里德几何学所不能描述的一大类复杂无规的几何对象。例如,弯弯曲曲的海岸线、起伏不平的山脉,粗糙不堪的断面,变幻无常的浮云,九曲回肠的河流,纵横交错的血管,令人眼花缭乱的满天繁星等。它们的特点都是,极不规则或极不光滑。直观而粗略地说,这些对象都是分形。(下面用代码画出的一个分形图形就很像错综复杂的血管壁的横截图)
————以上资料整理自百度百科
----------------------------------------------------------我是分割线-------------------------------------------------------------
下面我们来看一些分形图形实现的代码(written in java)
package cn.lucywong;
import java.awt.BorderLayout;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import javax.swing.JFrame;
import javax.swing.JPanel;
import cn.lucywong.DrawListener;
/**
* 递归分析画图
* @author LucyWong
*
*/
public class DrawFrame extends JFrame {
//声明一个DrawListener类对象
private DrawListener dl;
public static void main(String[] args) {
//实例化对象,调用初始化方法
DrawFrame df = new DrawFrame();
df.initUI();
}
public void initUI(){
//设置窗体属性值
this.setTitle("画板");
this.setSize(new Dimension(800,800));
this.setResizable(false);
this.setDefaultCloseOperation(3);
this.setLocationRelativeTo(null);
//创建中间绘制图形的面板对象,设置面板的背景色为白色
JPanel drawPanel = new JPanel();
drawPanel.setBackground(Color.WHITE);
this.add(drawPanel,BorderLayout.CENTER);
this.setVisible(true);//设置窗体可见必须放在最后
//窗体可见之后才可获取画笔,否则取到的是null
Graphics g = drawPanel.getGraphics();
//创建DrawListener类的对象
dl = new DrawListener(g);
//给事件源添加鼠标监听器方法,绑定事件接口对象
drawPanel.addMouseListener(dl);
drawPanel.addMouseMotionListener(dl);
}
}
package cn.lucywong;
import java.awt.Color;
import java.awt.Graphics;
import java.awt.event.MouseAdapter;
import java.awt.event.MouseEvent;
import java.util.Random;
public class DrawListener extends MouseAdapter {
//声明绘制图形的画笔对象名
private Graphics g;
/**
* 构造方法,可传参
* @param g
*/
public DrawListener(Graphics g) {
this.g = g;
}
@Override
public void mouseReleased(MouseEvent e) {
//绘图方法
//drawG1();
//drawG2();
drawG3();
}
public void drawG1(){
double x1 = 0,y1 = 0.5,temp;
int m,n;
double a = -2, b = -2,c = -1.2,d = 2;
for(int i = 0;i<100000;i++){
temp = x1;//将未改变的x1赋给temp以便计算y1
x1 = Math.sin(a*y1) - Math.cos(b*x1);
y1 = Math.sin(c*temp) - Math.cos(d*y1);
//测试用
//System.out.println(x1+" "+y1);
m = (int)((Math.sin(a*y1) - Math.cos(b*x1))*150+400);
n = (int)((Math.sin(c*x1) - Math.cos(d*y1))*150+400);
//m = (int)(x1*150+400);
//n = (int)(y1*150+400);
//测试用
//System.out.println(m+" "+n);
g.drawLine(m,n,m,n);
}
}
public void drawG2(){
double a = -1.40, b = 1.56,c = 1.40,d = -6.56;
double x1 = 2,y1 = 0,temp;
int m,n;
for(int i = 0; i<50000; i++){
temp = x1;
x1 = d * Math.sin(a*x1) - Math.sin(b*y1);
y1 = c * Math.cos(a*temp) + Math.cos(b*y1);
m = (int)((d*Math.sin(a*x1) - Math.sin(b*y1))*50+400);
n = (int)((c*Math.cos(a*x1) + Math.cos(b*y1))*50+300);
g.drawLine(m,n,m,n);
}
}
public void drawG3(){
//double a = 1, b = 4,c = 60;
//改变不同的参数画出的图形不一样
double a = 0.4, b = 1,c = 0;
double x1 = 0 , y1 = 0, temp;
int m , n;
for(int i =0 ;i<500000;i++){
temp = x1;
x1 = y1 - Math.signum(x1) * Math.sqrt((Math.abs(b*x1 - c)));
y1 = a - temp;
m = (int)(x1*150+400);
n = (int)(y1*150+300);
//m = (int)(x1*2+400);
//n = (int)(y1*2+300);
Random r = new Random();
g.setColor(new Color(r.nextInt(100),r.nextInt(256),r.nextInt(256)));
g.drawLine(m, n, m, n);
}
}
}
第一段是图形窗体的绘制,第二段是监听器和事件方法,其中drawG1( ),drawG2( ),drawG3( )是分别画出不同分形图形的方法,drawG3( )中使用不同的初始a,b,c参数的值画出的图形也不一样。
在第二段代码中,不同的点的x,y坐标是根据公式来计算的。我们需要给分形图形的初始点的坐标赋一个初值。其实,最开始我的想法是希望能够将获取的鼠标点击的坐标作为初始坐标,以此为中心来展开图形。但尝试过发现初值很大程度上会影响形状,往往事与愿违。所以最好的办法是自己试着赋一个初值,以便图形能够以一个恰当的比例显示在画板靠近中心的位置。
drawG1( )图形迭代公式:
在这里要强调一点,由于循环坐标x和y的值是不断被更新的,而且在第二行求y的值时,本来应该使用未改变的x,所以我们应该定义一个变量temp来保存之前的x,以便计算y。
temp = x1; //将未改变的x1赋给temp以便计算y1 x1 = Math.sin(a*y1) - Math.cos(b*x1); y1 = Math.sin(c*temp) - Math.cos(d*y1);
在后面画图的时候,要用x1而不是temp,否则图形不对。
m = (int)((Math.sin(a*y1) - Math.cos(b*x1))*150+400); n = (int)((Math.sin(c*x1) - Math.cos(d*y1))*150+400);
由于drawline( ) 函数的参数只能是整型变量,所以要用double型的x1,y1来计算精确的小数坐标,然后用另外的整形变量m和n来存储扩大和平移过的坐标,以便以合适的比例显示。
drawG2( )的迭代公式:
drawG3( )的迭代公式:
drawG1( )画出来的图如下所示:
有木有像像一根香蕉~
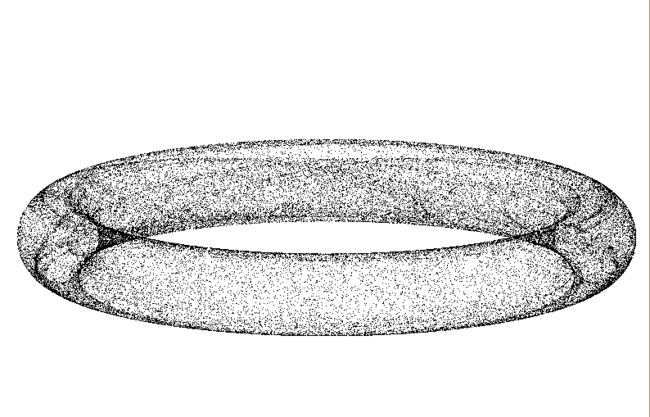
drawG2( )画出来的图如下所示:
这个像甜甜圈!~
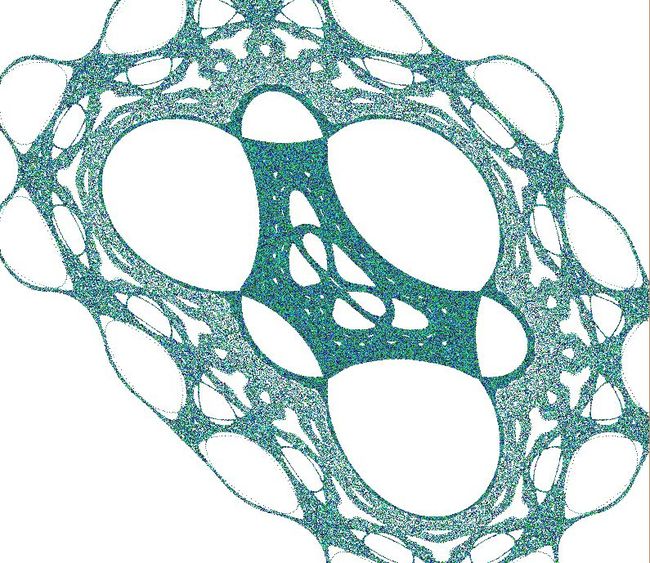
drawG3( )使用第一种参数设置:
这个就是我说的血管壁横截面_(:з」∠)_
使用第二种参数设置:
这让我想起来了小时候的万花筒,程序在执行时,从里向外又从外向里分形递归,感觉像是一株生长的海藻,很有生命力(我用setColor()给设了颜色)。
总而言之,有趣的分形图形有很多,我们自己也可以多多尝试一些类似的迭代公式,也可以上网去查找。像毕达哥拉斯树也会是不错的尝试选择。