CPM(Critical Path Method )

CPM(Critical Path Method ) is now widely used in projectmanagement to control the schedule of the project life cycle .

Now I will show you how to find out the critical activities andhow to create critical path from any project graph .

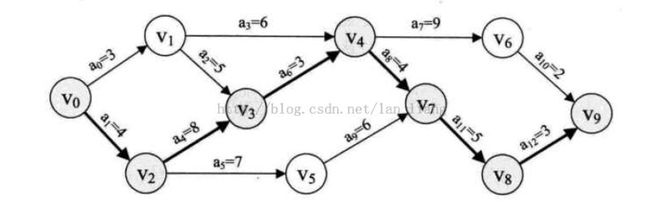
First , Let's see this graph :

Can see it has 9 activities and each number on line stands forhow many days taken to finish its task.

First ,We need to find out all the min-start time and max-endtime ,Let's store them into array .

Second , so we get 2 arrays , then we compare each elementbetween the 2 arrays ,select the elements that are equal. they are critical activities .

Third ,Join each elements ,we got the critical path.

now let's do it step by step .

First , We Need to get min-start time Array, meaning each activityminimum start time .

V[0] : 0

V[1] : Max(3) = 3

V[2] : Max(4) = 4

V[3] : Max(V[1]+5,V[2]+8) = Max(8,12) = 12

V[4] : Max(V[1]+6,V[3]+3) = 15

V[5] : Max(V[2]+7) = 11

V[6] : Max(V[4]+9) = 24

V[7] : Max(V[4] + 4,V[5] + 6) = Max(19,17) = 19

V[8] : Max(V[7] + 5) = 24

V[9] : Max(V[6] + 2,V[8] + 3) = Max(26,27) = 27

So the min-start time array is

{0,3,4,12,15,11,24,19,24,27}

Now Let's do with the max-end time array.

In min-start array V[9] = 27

so for max-end time array V[9] value is same ,So ,

V[9] = 27

V[8] = Min(V[9] - 3) = Min(24) = 24

V[7] = Min(V[8] - 5) = Min(19) = 19

V[6] = Min(V[9] - 2) = Min(25) = 25

V[5] = Min(V[7] - 6) = Min(13) = 13

V[4] = Min(V[6] - 9,V[7] - 4) = Min(16,15) = 15

V[3] = Min(V[4] - 3) = Min(12) = 12

V[2] = Min(V[3] - 8,V[5] - 7) = Min(4,6) = 4

V[1] = Min(V[4] - 6,V[3] - 5) = Min(9,7) = 7

V[0] = 0

So We got max-end array :

{0,7,4,12,15,13,25,19,24,27}

and min-start array:

{0,3,4,12,15,11,24,19,24,27}

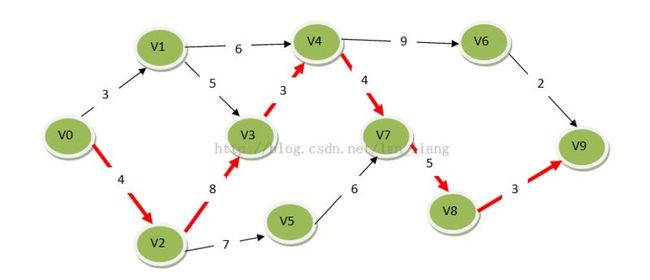
Now find the key-activities :

{0,4,12,15,19,24,27} , Mapping to nodes :

{V0,V2,V3,V4,V7,V8,V9}

Next ,Draw the key path :

Finish, Thanks for reading .