4-1 Mallet小波分解重构程序
Mallet小波在小波届的地位类似fft在傅立叶变化中的地位,在分解过程中先滤波后抽取,重构过程中先插值后滤波,可以操作正交小波变换和双正交小波变换。
本文中的程序是对构造的信号进行高低通滤波,之后再进行高低频重构,实现matlab中Mallet小波的基本操作。
%% 本程序采用Mallat算法对信号进行小波分析
clc;clear;
close all;
% 1 正弦波定义
f1= 50; % 频率1
f2= 100; % 频率2
fs= 2*(f1+f2); % 采样频率
Ts= 1/fs; % 采样间隔
N= 120; % 采样点数
n= 1:N;
y= sin(2*pi*f1*n*Ts)+ sin(2*pi*f2*n*Ts); % 正弦波混合
figure(1)
subplot(2,1,1)
plot(y);
title('原始信号');
subplot(2,1,2)
stem(abs(fft(y)));
title('原始信号频谱');
% 2 小波滤波器
h= wfilters('db30', 'l'); % 低通
g= wfilters('db30', 'h'); % 高通
h= [h,zeros(1,N-length(h))]; %补零(圆周卷积,且增大分辨率便于观察)
g= [g,zeros(1,N-length(g))]; %补零(圆周卷积,且增大分辨率便于观察)
figure(2);
subplot(2,1,1)
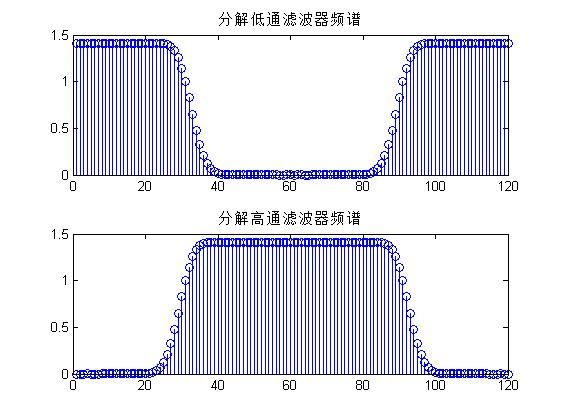
stem(abs(fft(h)));
title('分解低通滤波器频谱');
subplot(2,1,2)
stem(abs(fft(g)));
title('分解高通滤波器频谱');
% 3 Mallet分解算法(圆周卷积的快速傅立叶变换实现)
sig1= ifft(fft(y).*fft(h)); %低通
sig2= ifft(fft(y).*fft(g)); %高通
figure(3) % 信号图
subplot(2,2,1)
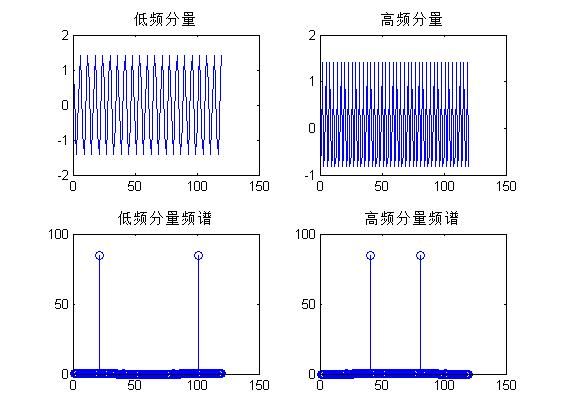
plot(real(sig1));
title('低频分量')
subplot(2,2,2)
plot(real(sig2));
title('高频分量')
subplot(2,2,3)
stem(abs(fft(sig1)));
title('低频分量频谱')
subplot(2,2,4)
stem(abs(fft(sig2)));
title('高频分量频谱')
% 4 Mallet重构算法
sig1= dyaddown(sig1); % 2抽取
sig2= dyaddown(sig2); % 2抽取
sig1= dyadup(sig1); % 2抽取
sig2= dyadup(sig2); % 2抽取
sig1= sig1(1, [1:N]); % 去掉最后一个零
sig2= sig2(1, [1:N]); % 去掉最后一个零
hr= h(end:-1:1); % 重构低通
gr= g(end:-1:1); % 重构高通
hr= circshift(hr',1)'; % 位置调整圆周右移以一位
gr= circshift(gr',1)'; % 位置调整圆周右移以一位
sig1= ifft(fft(hr).*fft(sig1)); % 低频
sig2= ifft(fft(gr).*fft(sig2)); % 高频
sig= sig1+ sig2; % 源信号
% 5 比较
figure(4);
subplot(2,2,1);
plot(real(sig1));
title('重构低频信号');
subplot(2,2,2);
plot(real(sig2));
title('重构高频信号');
subplot(2,2,3);
stem(abs(fft(sig1)));
title('重构低频信号频谱');
subplot(2,2,4);
stem(abs(fft(sig2)));
title('重构高频信号频谱');
figure(5)
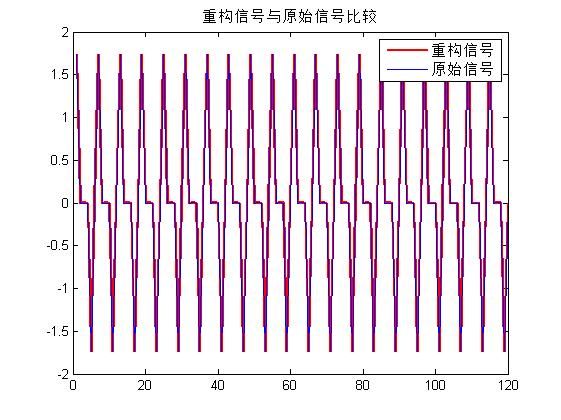
plot(real(sig),'r','linewidth',2);
hold on
plot(y)
legend('重构信号','原始信号');
title('重构信号与原始信号比较')
程序运行结果
问题:
1 wfilters函数
功能:生成四种小波滤波器,高低通滤波器,高低频重构滤波器
格式:[LO_D,HI_D,LO_R,HI_R] = WFILTERS('wname')
[F1,F2] = WFILTERS('wname','type')
说明:LO_D - 低通滤波器
HI_D - 高通滤波器
LO_R - 低通重构滤波器
HI_R - 高通重构滤波器
type:
LO_D and HI_D if 'type' = 'd' (分解)
LO_R and HI_R if 'type' = 'r' (重构)
LO_D and LO_R if 'type' = 'l' (低通滤波器)
HI_D and HI_R if 'type' = 'h' (高通滤波器)
wname:
wname说明
示例:使用中如果信号长度和滤波器的长度不一致,需要将滤波器补零
h= wfilters('db30', 'l'); % 低通
g= wfilters('db30', 'h'); % 高通
h= [h,zeros(1,N-length(h))]; %补零(圆周卷积,且增大分辨率便于观察)
g= [g,zeros(1,N-length(g))]; %补零(圆周卷积,且增大分辨率便于观察)
figure(2);
subplot(2,1,1)
stem(abs(fft(h)));
title('分解低通滤波器频谱');
subplot(2,1,2)
stem(abs(fft(g)));
title('分解高通滤波器频谱');
2 圆周卷积
线性卷积就是多项式系数乘法:设a的长度是M,b的长度是N,则a卷积b的长度是M+N-1,运算参见多项式乘法。
“L点的圆周卷积”就是把先做线性卷积,再把结果的前L点保留不动,后面的点截下来,加到结果的头上去。如果L>M+N-1,则线性卷积和圆周卷积相同。----来自百度知道
圆周卷积 线性卷积 周期卷积
3 抽样函数
dyaddown
功能:对时间序列进行二元采样,每隔一个元素提取一个元素,得到一个降采样时间序列。
格式:
1.y = dyaddown(x, EVENODD)
当EVENODD=0时,从x中第二个元素开始采样(偶采样);当EVENODD=1时,从x中第一个元素开始采样(奇采样)。
2.y = dyaddown(x)
EVENODD缺省,按EVENODD=0
dyadup
功能:对时间序列进行二元插值,每隔一个元素插入一个0元素,得到一个时间序列。
格式:
1.y = dyadup(x, EVENODD)
当EVENODD=0时,从x中第二个元素开始采样(偶采样);当EVENODD=1时,从x中第一个元素开始采样(奇采样)。
2.y = dyadup(x)
EVENODD缺省,按EVENODD=0