【matlab】2014年IMO第四题解答
看题!
补充一下,三角形ABC是锐角三角形。
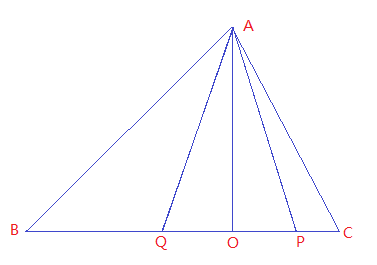
先证明一个引理:AO垂直于BC,角QAO 等于 角 PAO。
证明如下 :
角CAO + 角QAO = 角B
角BAO + 角PAO = 角C
即:
90 - 角C + 角QAO = 角B
90 - 角B + 角PAO = 角C
即 角QAO = 角PAO = 角B + 角C - 90
因为三角形ABC是锐角三角形, 角B + 角C - 90必然大于零。
可以开始证明了。
先说基本思路,要证明四点共圆,那么只要证明以这四点为顶点的四边形对角互补即可。
两个角互补,那么它俩的正切值互为相反数。我们来求这俩正切值。
以O为原点,建立直角坐标系。
打开matlab,定义变量:
syms a syms b syms c A = [0, a] B = [b, 0] C = [c, 0]
设点P的横坐标为 p,
则直线AP的斜率为 -a/p,直线AB的斜率为-a/b,直线AC的斜率为-a/c。
两条直线的斜率为k1 和 k2,那么它们夹角的斜率的绝对值就是 |k1 - k2|/|1 + k1 * k2|
解方程:
[point_p] = solve( '(a/b - a/p) / (1 + a/p * a/b) = a/c ', 'p' ) P = [point_p, 0] Q = [-point_p, 0] #注意,这一步用了我们的引理。
解得:P =
[ -(c*b+a^2)/(-c+b), 0]
注意,这一步涉及到绝对值运算,方程的正负号需要留心。
因为P Q 是 AM AN的中点,因此有:
M = 2*P - A N = 2*Q - A
写一个计算斜率的函数,输入为两个点,输出为经过这两点直线的斜率
function k = k_line(A, B) tmp = A - B k = tmp(2)/tmp(1)
开始计算相关直线的斜率:
#直线BM的斜率 k_BM = k_line(M, B) #直线CN的斜率 k_CN = k_line(C, N) #直线AB的斜率 k_AB = -a/b #直线AC的斜率 k_AC = -a/c #用斜率公式,计算出来的角ABM的正切值 k_left = (k_AB - k_BM)/(1 + k_AB * k_BM) #用斜率公式,计算出来的角ACN的正切值 k_right = (k_AC - k_CN)/(1 + k_AC * k_CN)
注意最后两个值,如果这两个角互补,那么这俩值的绝对值相等,
我们算出的结果要么相等,要么互为相反数。
输入代码运算结果如下:
k_left = (-a/b+a/(-2*(c*b+a^2)/(-c+b)-b))/(1+a^2/b/(-2*(c*b+a^2)/(-c+b)-b)) k_right = (-a/c-a/(c-2*(c*b+a^2)/(-c+b)))/(1-a^2/c/(c-2*(c*b+a^2)/(-c+b))) #化简: simplify(k_left) ans = -2*a/(b+c) simplify(k_right) ans = -2*a/(b+c)
二者相等。
ok!证明完毕。
完整的代码如下:
clear syms a syms b syms c A = [0, a] B = [b, 0] C = [c, 0] [point_p] = solve( '(a/b - a/p) / (1 + a/p * a/b) = a/c ', 'p' ) P = [point_p, 0] Q = [-point_p, 0] M = 2*P - A N = 2*Q - A k_BM = k_line(M, B) k_CN = k_line(C, N) k_AB = -a/b k_AC = -a/c k_left = (k_AB - k_BM)/(1 + k_AB * k_BM) k_right = (k_AC - k_CN)/(1 + k_AC * k_CN) #记得创建一个M文件,内容如下: function k = k_line(A, B) tmp = A - B k = tmp(2)/tmp(1)