Clustering by density peaks and distance
这次介绍的是Alex和Alessandro于2014年发表在的Science上的一篇关于聚类的文章[13],该文章的基本思想很简单,但是其聚类效果却兼具了谱聚类(Spectral Clustering)[11,14,15]和K-Means的特点,着实激起了我的极大的兴趣,该聚类算法主要是基于两个基本点:
- 聚类中心的密度高于其临近的样本点的密度
- 聚类中心与比其密度还高的聚类中心的距离相对较大
基于这个思想,聚类过程中的聚类中心数目可以很直观的选取,离群点也能被自动检测出来并排除在聚类分析外。无论每个聚类的形状是什么样的,或者样本点的维度是多少,聚类分析的结果都能令人很满意。下面我会主要基于这篇文章来详述该聚类算法的来龙去脉,并简单回顾下相关的聚类算法。
聚类算法回顾
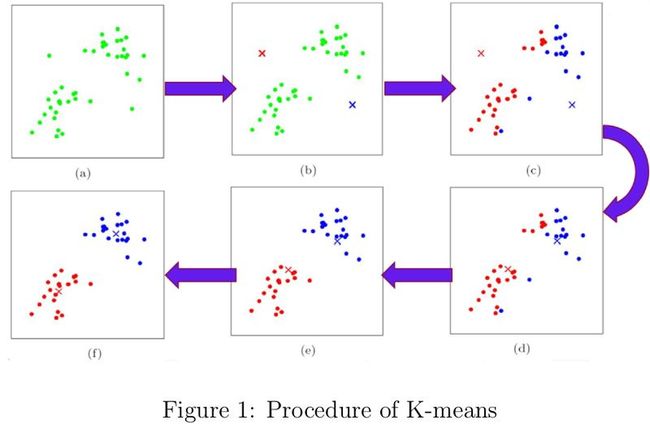
众所周知,聚类分析目的在于根据样本之间的相似性将样本划为不同的类簇,但聚类的科学定义貌似在学术界还未达成共识。论文[17]对聚类算法进行了综述,发现有好多聚类算法我还没学习。在K-means和K-medoids中,每个类簇都由一组到各自的聚类中心距离最近的数据组成。两者的目标函数形式为各样本点到对应的聚类中心的距离之和,经过反复的更新聚类中心和重新为样本点分配聚类中心的过程直至收敛,如图1所示。两者的区别在于,K-means的聚类中心为属于该类簇的所有样本点的均值,而K-medoids的聚类中心为该类簇中离所有样本点的聚类之和最小的样本点。这两者聚类算法实现起来都非常简单,对于紧凑型的和呈超球体状分布的数据非常适用。但两者的缺陷也很明显:
- 缺乏能确定类簇数目和进行初步划分的有效机制;
- 迭代优化的策略无法保证全局最优解;
- 对离群点和噪声非常敏感
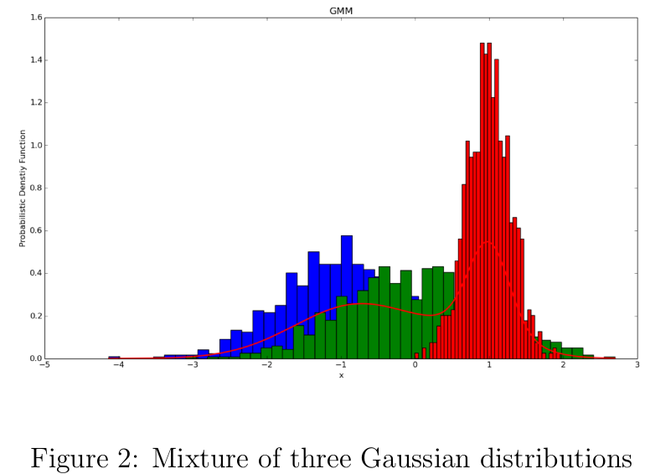
在基于概率密度的聚类算法中,我们会假设各类簇由不同的概率密度函数产生(如图2),而每个样本点则是以不同的权重服从这些概率分布的。很不幸的是,在这类算法中用最大似然估计求解参数往往不可行,只能用迭代求解的方式获得一个次优解,而期望最大化(Expectation Maximization,EM)是最常用的一个策略。在这类算法中,最典型的莫过于高斯混合模型(Gaussian Mixture Model,GMM)[12]。这类算法的准确度取决于预先定义的概率分布能否很好的拟合训练数据,但问题在于很多情况下我们无法知晓数据在整体上或者局部上到底近似于什么样的概率分布。
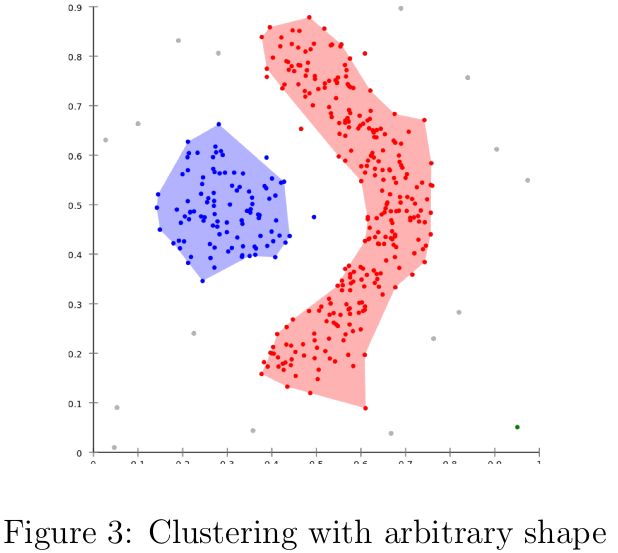
基于局部密度的聚类算法可以很容易地检测出任意形状的类簇。在DBSCAN[10]中,需要用户给定密度阈值和领域半径作为参数,在领域半径内的密度小于该阈值的样本点被视为噪声点,剩下的密度较高的非连通区域则被分配到不同的类簇中,其伪代码如下所示。但是选择合适的密度阈值并不是那么容易的事情,有关的参数估计建议可参见[3]。DBSCAN的优点[3]总结如下:
- 无需预先指定类簇的数目;
- 可以发现任意形状的类簇,如图3所示;
- 可以检测出噪声点,且对噪声点鲁棒性较强;
- 除了边界点外,聚类结果(核心点与噪声点)与样本点的遍历顺序无关
DBSCAN的缺点[3]总结如下:
- 针对边界点而言,DBSCAN的聚类结果并非完全确定的。幸运的是这种情况并非频繁出现,而且对聚类的结果影响很小。如果把边界点也当成噪声点处理,那么聚类结果就具有确定性。
- 聚类结果依赖于距离度量规则。最常用的欧式距离在高维空间里由于“维度灾难”几乎无法发挥有效作用,使得设定合适的搜寻半径更为困难。
- 不适用于密度差异很大的数据集,因为此时各个类簇的搜寻半径和密度阈值都不相同,使得参数的选取更为困难。
DBSCAN(D, eps, minPts)
//eps:search radius
//minPts:density threshold
C = 0
for each unvisited point P in dataset D
mark P as visited
NeighborPts = regionQuery(P, eps)
if sizeof(NeighborPts) < minPts
mark P as NOISE
else
C = next cluster
expandCluster(P, NeighborPts, C, eps, MinPts)
expandCluster(P, NeighborPts, C, eps, minPts)
add P to cluster C
for each point Q in NeighborPts
if Q is not visited
mark Q as visited
NeighborPts' = regionQuery(Q, eps)
if sizeof(NeighborPts') >= minPts
NeighborPts = NeighborPts joined with NeighborPts'
if Q is not yet member of any cluster
add Q to cluster C
regionQuery(P, eps)
return all points within P's eps-neighborhood (including P)
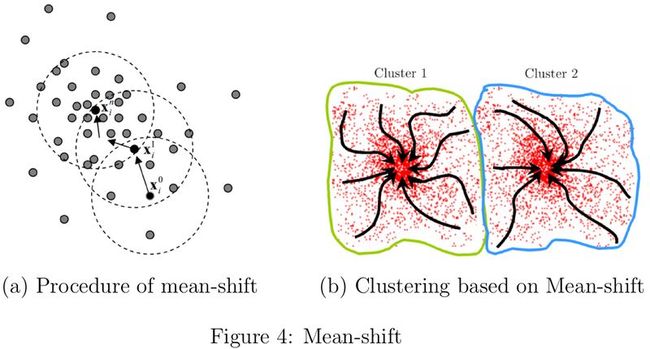
基于均值漂移(Mean-shift)[5,7,9]的聚类算法则无需为搜索半径和密度阈值的设定而烦恼,不过也面临bandwidth的选取问题,关于怎么设定bandwidth的研究可参见[8,16]。Mean-sift的基本思路就是从初始点出发,以梯度上升的方式不断寻找核密度估计函数的局部最大值直至收敛(如图4(a)所示),这些驻点代表分布的模式。在基于mean-shift的聚类算法中,依次以每一个样本点作为mean-shift的起始点,然后将其移至核密度估计函数的某个局部驻点,最后近似收敛到同一个驻点的所有样本被划分至同一个类簇,如图4(b)所示。总体而言,在基于密度的聚类算法中,类簇可被定义为收敛到相同的密度分布函数局部极大值的样本点的集合。
基于密度峰值和距离的聚类算法
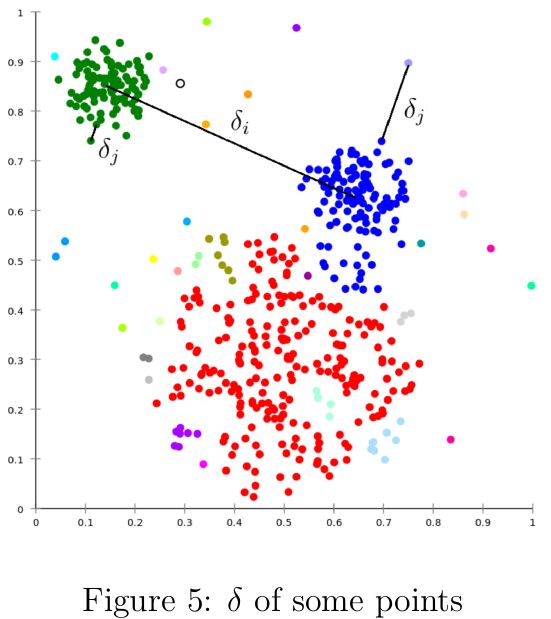
该聚类算法的假设前提是聚类中心周围的样本点的局部密度低于聚类中心的局部密度,并且聚类中心与比其局部密度更高的点之间的距离相对较大。其聚类效果与DBSCAN和mean-shift类似,可以检测出非球体的类簇。作者号称可以自动找到类簇的数目,虽然文中给了一点相关的寻找聚类数目的思路,但是提供的Matlab代码中没有实现该思路,还是需要人工选择聚类中心,所以在相关评论[2]中“自动”一词遭到了质疑。与mean-shift类似,聚类中心定义为局部密度最大值点;与mean-shift不同的是,聚类中心是某个特定样本点,并且无需在核函数定义的空间内针对每个样本点显式求解局部密度最大的点。 给定数据集\(\mathcal{S}=\{x_i|x_i\in\mathbb{R}^n,i=1,\cdots,N\}\),对于每一个样本点\(x_i\)计算两个量化值:局部密度值\(\rho_i\)和距离密度更高的样本点的聚类\(\delta_i\)。\(x_i\)的局部密度\(\rho_i\)定义如为: \begin{equation} \rho_i=\sum_{j=1}^N\chi(d_{ij}-d_c) \end{equation} 其中\(d_c\)为截断距离(cutoff distance),其实就是领域的搜索半径;\(d_{ij}\)为\(x_i\)与\(x_j\)之间的距离;函数\(\chi(x)\)定义为 \begin{equation} \chi(x)=\begin{cases} 1,& \text{if \(x<0\)};\\ 0,& otherwise. \end{cases} \end{equation} 根据这篇文章的评论[2],发现还有两个密度的度量方法也是很有价值的.第一个是用样本点与最近的\(M\)个邻居的距离的均值的负数来描述;另一个就是高斯核函数来度量,会比用截断距离度量鲁棒性更强一些. \begin{equation} \rho(x_i)=-\frac{1}{M}\sum_{j:j\in KNN(x_i)}d_{ij} \label{eq:avg_kernel} \end{equation} \begin{equation} \rho(x_i)=\sum_{j=1}^N\exp(-\frac{d_{ij}^2}{\sigma}) \label{eq:gauss_kernel} \end{equation} 实际上,上述的\(\rho_i\)定义的就是与\(x_i\)之间的距离小于\(d_c\)的样本点的数目。距离\(\delta_i\)度量\(x_i\)与比其密度高的最近的样本点之间的距离;如果\(\rho_i\)为最大值,则\(\delta_i\)为与离\(x_i\)最远样本之间的距离: \begin{equation} \delta_i=\begin{cases} \underset{j:\rho_j>\rho_i}{\min}(d_{ij}), & \text{if \(\exists j,\rho_j>\rho_i\)};\\ \underset{j}{\max}(d_{ij}), & otherwise. \end{cases} \end{equation} 对于密度值为局部或全局最大的样本点而言,它们的\(\delta_i\)会比其他样本点的\(\delta_j\)值要大很多(如图5所示),因为前者代表局部密度最大的样本点之间的距离,而后者代表样本点与其对应的局部密度最大的样本点之间的距离。因此,那些\(\delta\)值很大的样本点也很有可能就是聚类中心。
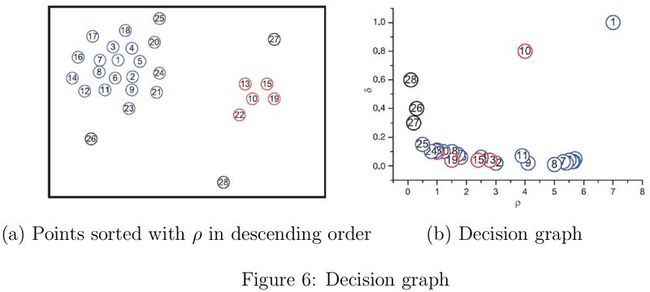
论文中给出了一个示例,如图6(a)所示,图中一共有28个样本点,样本点按照密度降序排列。从图中大致可以观察到有两个类簇,剩下的26、27和28号样本点可被视为离群点。在图6(b)中,分别以对判定是否为聚类中的最关键信息\(\rho\)和\(\delta\)为横纵坐标绘制决策图(decision graph),看到1和10号样本点位于决策图的最右上角。9和10号样本点虽然密度值\(\rho\)非常接近,但是\(\delta\)值却相差很大;被孤立的26、27和28号样本点虽然\(\delta\)值较大,但是\(\rho\)值很小。综上可知,只有\(\rho\)值很高并且\(\delta\)相对较大的样本点才会是聚类中心。
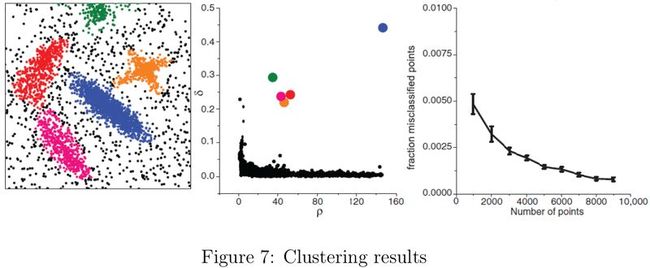
在找出聚类中心后,接下来就是将所有剩下的点划分到比其密度更高且最近的样本点所属的类簇中,当然经过这一步之后暂时会为噪声点也分配到类簇中。在聚类分析中,经常还会进一步分析类簇分配的可靠性。在DBSCAN中,只考虑了密度高于密度阈值的可靠性高一些的样本点,但是会出现较低密度的类簇被误认为噪声的情况。文中取而代之的是为每个类簇引入边界区域的概念。边界区域的密度值\(\rho_b\)会根据属于这个类簇并且与属于其他类簇的样本点之间的距离小于\(d_c\)的成员计算出来。对于每个类簇中的所有样本点,密度值高于\(\rho_b\)的被视为类簇的核心组成部分(cluster core),剩下的则被视为该类簇的光晕(cluster halo),类簇光晕中则包含噪声点。论文中给出了一个聚类的结果,如图7所示。
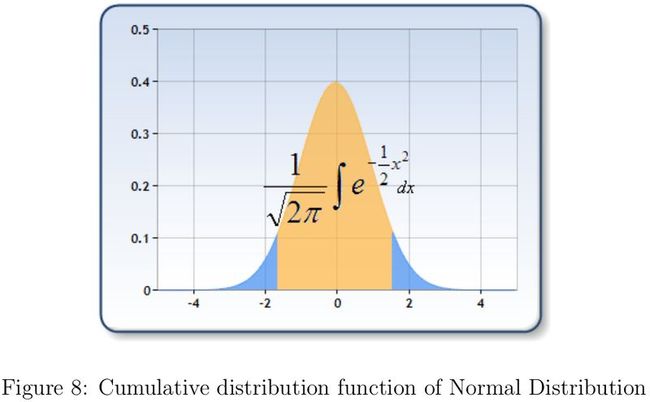
邻域搜索半径\(d_c\)到底如何取值呢?\(d_c\)显然是对聚类结果又影响的,这一点我们仅需要考虑两个最极端的情形就明白了。如果\(d_c\)太大,那么每个数据点的密度值都近似相等,导致所有数据点被划分至同一个类簇中;如果\(d_c\)太小,每个类簇包含的样本点会很少,很有可能出现同一个类簇被分割成好几部分的情况。另一方面,不同的数据集中数据点之间的密集程度不同,那么想给出一个适合所有数据集的\(d_c\)是不可能的。作者在文中提出,合适的\(d_c\)应该使数据点的平均近邻数目占整个数据集规模的比例为\(\tau,(\tau=1\%\sim 2\%)\)。如此一来,参数\(\tau\)就独立于特定数据集了。针对每个数据集,我们都可以寻找一个比较合适的\(d_c\)。结合作者给出的Matlab代码,分析后可知具体的计算方法如下:取出对称的距离矩阵的上三角所有的\(M=N(N-1)/2\)个元素,然后对其进行升序排列\(d_1\leq d_2\leq \cdots\leq d_M\)。为了保证平均每个数据点的近邻点数目所占比例为\(\tau\),那么只要保证小于\(d_c\)的距离数目所占比例也为\(\tau\)即可,因此取\(d_c=d_{round(\tau M)}\)。 类簇的数目该如何确定呢?作者给Matlab代码中,聚类中心是需要人工选定的,很多读者因此质疑文中的"it is able to detect nonspherical clusters and to automatically find the correct number of clusters",是不是有种被欺骗的感觉。不过作者在文中也给出了一个简单选择类簇的数目,虽然我也觉得该方法存在一些问题,但总归还是给出了解决方案的。由前面解释的论文的两个基本立足点可知,聚类中心对应的\(\rho\)和\(\delta\)都是比较大的。作者为每个样本点\(x_i\)引入\(\gamma_i=\rho_i\delta_i\),然后将所有的\(\gamma_i\)降序排列后显示在图9(a)。如果分别对\(\rho\)和\(\delta\)先做归一化处理后会更合理一些,这样也会使得两者参与决策的权重相当。因为如果\(\rho\)和\(\delta\)的不在一个数量级,那么必然数量级小带来的的影响会很小。接下来怎么办呢?作者依然没有给出具体的解决方案。因为整体而言,\(\gamma\)的值在大多数情况下还是很相近的,差异比较大的就是那几个聚类中心,我觉得可以从异常检查(Anomaly Detection)的角度去寻找这个跳跃点。最简单方法,可以根据相邻\(\gamma\)的值构建一个高斯分布\(\mathbb{N}(\mu,\sigma^2)\),根据最大似然参数估计法,该高斯分布的参数只需扫描两遍\(\gamma\)的值即可,所以模型还是很效率还是很高的。有了这个模型后,我们从后往前扫描\(\gamma\)的值,如果发现某个值的左边或右边的累积概率(如图8的左右两侧蓝色区域)小于阈值(比如0.005)时就判定找到了异常的跳跃点,此时就能大致确定类簇的数目了。若想进一步学习如何利用高斯分布进行异常检测可参见[1]。 我们都知道高斯分布的概率密度函数,可是高斯分布的累积分布函数(Cumulative Distribution Function)不存在初等函数的表达形式,那该如何是好?查找了半天资料,也没找到如何数值逼近的原理说明,不过搜到了一段用java编写的基于Hart Algorithm近似计算标准正态分布的累积分布函数的代码[4]。寥寥数行java代码就搞定了,但是我暂时没理解为什么这么做是可行的。我将其转换成了如下的C++代码,然后将输出结果和维基百科上的Q函数表[6]中的数据对比分析(注意\(1-Q(x)=\Phi(x)\)),发现结果和预期的一模一样,简直把我惊呆了。
double CDFofNormalDistribution(double x)
{
const double PI=3.1415926;
double p0=220.2068679123761;
double p1=221.2135961699311;
double p2=112.0792914978709;
double p3=33.91286607838300;
double p4=6.373962203531650;
double p5=.7003830644436881;
double p6=.03326249659989109;
double q0=440.4137358247552;
double q1=793.8265125199484;
double q2=637.3336333788311;
double q3=296.5642487796737;
double q4=86.78073220294608;
double q5=16.06417757920695;
double q6=1.755667163182642;
double q7=0.08838834764831844;
double cutoff=7.071;//10/sqrt(2)
double root2pi=2.506628274631001;//sqrt(2*PI)
double xabs=abs(x);
double res=0;
if(x>37.0)
res=1.0;
else if(x<-37.0)
res=0.0;
else
{
double expntl=exp(-.5*xabs*xabs);
double pdf=expntl/root2pi;
if(xabs<cutoff)
res=expntl*((((((p6*xabs + p5)*xabs + p4)*xabs + p3)*xabs+ \
p2)*xabs + p1)*xabs + p0)/(((((((q7*xabs + q6)*xabs + \
q5)*xabs + q4)*xabs + q3)*xabs + q2)*xabs + q1)*xabs+q0);
else
res=pdf/(xabs+1.0/(xabs+2.0/(xabs+3.0/(xabs+4.0/(xabs+0.65)))));
}
if(x>=0.0)
res=1.0-res;
return res;
}
此外,作者声称根据随机均匀分布生成的数据对应的\(\gamma\)服从幂律分布(Power laws),但是真正具备聚类中心的数据集是不存在这种情况的。很多现象其实都是近似服从幂律分布的,尤其适用于大多数事件的规模很小但少数事件规模很大的场合,不过作者在此并未给出该定论的出处,所以同样这一点遭到了很多读者的质疑。我猜目前只是作者根据一些实验数归纳出来的,只能说是靠不完全统计得到的经验,没有实质性的理论依据。也就是\(\gamma\approx cr^{-k}+\epsilon\),其中\(r\)为\(\gamma\)的排名序号,那么\(\log\gamma\)和\(\log r\)之间应该近似呈现线性关系,如图9(b)所示。如果作者的猜测正确的话,我们不妨在聚类前汇出如\(\log\gamma\)和\(\log r\)的关系图,借此判断聚类的复杂性,或者说在该数据集上进行聚类的结果可靠性如何。
最后,基于这篇文章思想,我最终用C++代码实现了一个比较完整的聚类算法,并作为我在GitHub上的first repository上传到了GitHub上面,有需要的请前往https://github.com/jeromewang-github/cluster-science2014下载,欢迎大家找出bug和提供修改意见!
References
- [1] Anomaly detection. http://www.holehouse.org/mlclass/15_Anomaly_Detection.html.
- [2] Comments on clustering by fast search and find of density peaks. http://comments.sciencemag.org/content/10.1126/science.1242072.
- [3] Dbscan. http://en.wikipedia.org/wiki/DBSCAN.
- [4] Hart algorithm for normal cdf. http://www.onedigit.org/Home/quantitative-finance/hart-algorithm-for-normal-cdf.
- [5] Mean-shift. http://en.wikipedia.org/wiki/Mean-shift.
- [6] Q-function. http://en.wikipedia.org/wiki/Q-function.
- [7] Dorin Comaniciu and Peter Meer. Mean shift: A robust approach toward feature space analysis. Pattern Analysis and Machine Intelligence, IEEE-Transactions on, 24(5):603–619, 2002.
- [8] Dorin Comaniciu, Visvanathan Ramesh, and Peter Meer. The variable bandwidth mean shift and data-driven scale selection. In Computer Vision, 2001. ICCV 2001. Proceedings. Eighth IEEE International Conference on, volume 1, pages 438–445. IEEE, 2001.
- [9] Konstantinos G. Derpanis. Mean shift clustering. http://www.cse.yorku.ca/~kosta/CompVis_Notes/mean_shift.pdf, 2005.
- [10] Martin Ester, Hans-Peter Kriegel, J ̈org Sander, and Xiaowei Xu. A density-based algorithm for discovering clusters in large spatial databases with noise. In Kdd, volume 96, pages 226–231, 1996.
- [11] Andrew Y Ng, Michael I Jordan, Yair Weiss, et al. On spectral clustering: Analysis and an algorithm. Advances in neural information processing systems, 2:849–856, 2002.
- [12] Douglas Reynolds. Gaussian mixture models. Encyclopedia of Biometrics, pages 659–663, 2009.
- [13] Alex Rodriguez and Alessandro Laio. Clustering by fast search and find of density peaks. Science, 344(6191):1492–1496, 2014.
- [14] Aarti Singh. Spectral clustering. https://www.cs.cmu.edu/~aarti/Class/10701/slides/Lecture21_2.pdf.
- [15] Ulrike Von Luxburg. A tutorial on spectral clustering. Statistics and computing, 17(4):395–416, 2007.
- [16] Jue Wang, Bo Thiesson, Yingqing Xu, and Michael Cohen. Image and video segmentation by anisotropic kernel mean shift. In Computer Vision-ECCV 2004, pages 238–249. Springer, 2004.
- [17] Rui Xu, Donald Wunsch, et al. Survey of clustering algorithms. Neural Networks, IEEE Transactions on, 16(3):645–678, 2005.