Javascript图像处理——仿射变换
前言
上一篇文章,我们讲解了图像金字塔,这篇文章我们来了解仿射变换。
仿射?!
任何仿射变换都可以转换成,乘以一个矩阵(线性变化),再加上一个向量(平移变化)。
实际上仿射是两幅图片的变换关系。
例如我们可以通过仿射变换对图片进行:缩放、旋转、平移等操作。
一个数学问题
在解决仿射问题前,我们来做一个数学题。
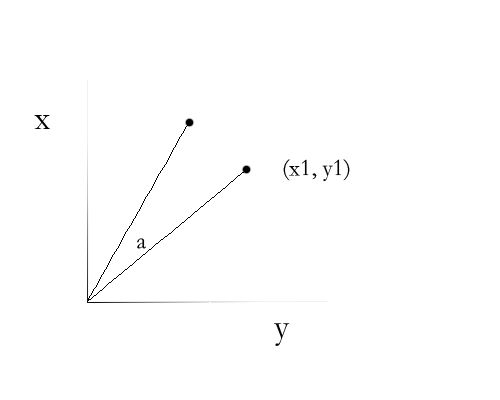
如图,对于点(x1, y1),相对于原点旋转一个角度a,那么这个点到哪里了呢?
我们将坐标系变成极坐标系,则点(x1, y1)就变成了(r, β),而旋转后变成(r, α + β)。
转回直角坐标系,则旋转后的点变成了(cos(α + β) * r, sin(α + β) * r)。
然后利用公式:
cos(α+β)=cosαcosβ-sinαsinβ
sin(α+β)=sinαcosβ+cosαsinβ
以及原来点为(cosβ * r, sinβ * r),于是很容易得出新的点为(x1 * cosα - y1 * sinα, x1 * sinaα + y1 * cosα)。
我们可以从中推导出旋转变换公式:
那么平移就相对简单很多了,就相当于加上一个向量(c, d)就行了。
获得变换矩阵函数实现
通常我们使用矩阵来表示仿射变换。
其中A是旋转缩放变换,B是平移变换。则结果T满足:
或者
即:
var getRotationArray2D = function(__angle, __x, __y){ var sin = Math.sin(__angle) || 0, cos = Math.cos(__angle) || 1, x = __x || 0, y = __y || 0; return [cos, -sin, -x, sin, cos, -y ]; };
这样我们就得到了一个仿射变换矩阵。
当然这个实现本身是有一定问题的,因为这个原点被固定在左上角了。
仿射变换实现
var warpAffine = function(__src, __rotArray, __dst){ (__src && __rotArray) || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */); if(__src.type && __src.type === "CV_RGBA"){ var height = __src.row, width = __src.col, dst = __dst || new Mat(height, width, CV_RGBA), sData = new Uint32Array(__src.buffer), dData = new Uint32Array(dst.buffer); var i, j, xs, ys, x, y, nowPix; for(j = 0, nowPix = 0; j < height; j++){ xs = __rotArray[1] * j + __rotArray[2]; ys = __rotArray[4] * j + __rotArray[5]; for(i = 0; i < width; i++, nowPix++, xs += __rotArray[0], ys += __rotArray[3]){ if(xs > 0 && ys > 0 && xs < width && ys < height){ y = ys | 0; x = xs | 0; dData[nowPix] = sData[y * width + x]; }else{ dData[nowPix] = 4278190080; //Black } } } }else{ error(arguments.callee, UNSPPORT_DATA_TYPE/* {line} */); } return dst; };
这个函数先把矩阵数据变成32位形式,操作每个元素就等同于操作每一个像素。
然后遍历所有元素,对对应的点进行赋值。
效果
系列目录