遗传算法(GA)学习笔记---旅行商问题(TSP)
一、步骤:
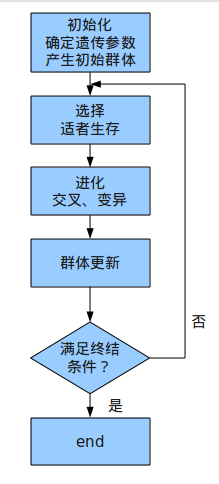
二、重点:
1、编码
由于遗传算法不能直接处理问题空间的数据,所以我们必须将问题空间的数据映射成遗传空间的基因型串结构数据,而算法程序是可以处理遗传空间的基因型 串结构数据的。比如现在要计算北京、天津、广东、新疆这四个城市的一条最优路径,但算法程序不能够直接处理北京、天津、广东、新疆这些数据,所以我们得给 它们编上号,北京(0)、天津(1)、广东(2)、新疆(3),路径(天津->新疆->北京->广东)可以表示成基因型串结构数据 (1302),这样算法程序只要直接处理它们的编号就行了。
(1)二进制编码,基因用0或1表示(常用于解决01背包问题)
如:基因A:00100011010 (代表一个个体的染色体)
(2)互换编码(用于解决排序问题,如旅行商问题和调度问题)
如旅行商问题中,一串基因编码用来表示遍历的城市顺序,如:234517986,表示九个城市中,先经过城市2,再经过城市3,依此类推。
(3)树形编码(用于遗传规划中的演化编程或者表示)
如问题:给定了很多组输入和输出。请你为这些输入输出选择一个函数,使得这个函数把每个输入尽可能近地映射为输出。
编码方法:基因就是树形结构中的一些函数。
(4)值编码 (二进制编码不好用时,解决复杂的数值问题)(源代码中使用类似此方法)
在值编码中,每个基因就是一串取值。这些取值可以是与问题有关任何值:整数,实数,字符或者其他一些更复杂的东西。
2、适应度函数
遗传算法对一个个体(解)的好坏用适应度函数值来评价,适应度函数值越大,解的质量越好。适应度函数是遗传算法进化过程的驱动力,也是进行自然选择的唯一标准,它的设计应结合求解问题本身的要求而定。
如TSP问题,遍历各城市路径之和越小越好,这样可以用可能的最大路径长度减去实际经过的路径长度,作为该问题的适应度函数。
3、选择
在进化中,适者生存,所以在遗传算法运行过程中,会不断地选择优者保留下来,同时也不断地选择劣者淘汰下去。选择算子有很多种方法,以下是比较简单常见的方法:
(1)排序选择方法(源代码中使用类似此方法)
排序选择方法是指在计算每一个个体的适应度(源代码中将路径总长度当适应度)之后,根据适应度大小对个体排序,然后按照事先设置好的概率表按序分配给个体,作为个自的选择概率。
(2)适应度比例方法
适应度比例方法是目前遗传算法中最基本也是最常用的选择方法,即各个个体的选择概率和其适应度值成正比。
(3)最佳个体保留方法
即把群体中适应度最高的个体不进行交叉而直接复制到下一代。
4、交叉
生物进化的核心作用是生物遗传基因的重组,相对应,遗传算法的核心操作是交叉算子,所谓交叉是指两个或两个以上的父代个体的部分结构加以替换重组而生成新个体的操作。
(1)单交叉点法 (用于二进制编码)
选择一个交叉点,子代在交叉点前面的基因从一个父代基因那里得到,后面的部分从另外一个父代基因那里得到。
如:交叉前:
00000|01110000000010000
11100|00000111111000101
交叉后:
00000|00000111111000101
11100|01110000000010000
(2)双交叉点法 (用于二进制编码)
选择两个交叉点,子代基因在两个交叉点间部分来自一个父代基因,其余部分来自于另外一个父代基因.
如:交叉前:
01 |0010| 11
11 |0111| 01
交叉后:
11 |0010| 01
01 |0111| 11
(3)基于“ 与/或 ”交叉法 (用于二进制编码)
对父代按位"与”逻辑运算产生一子代A;按位”或”逻辑运算产生另一子代B。该交叉策略在解背包问题中效果较好 .
如:交叉前:
01001011
11011101
交叉后:
01001001
11011111
(4)单交叉点法 (用于互换编码)
选择一个交叉点,子代的从初始位置出发的部分从一个基因复制,然后在另一个基因中扫描,如果某个位点在子代中没有,就把它添加进去。
如:交叉前:
87213 | 09546
98356 | 71420
交叉后:
87213 | 95640
98356 | 72104
(5)部分匹配交叉(PMX)法(用于互换编码)
先随机产生两个交叉点,定义这两点间的区域为匹配区域,并用交换两个父代的匹配区域。
父代A:872 | 130 | 9546
父代B:983 | 567 | 1420 变为:
TEMP A: 872 | 567 | 9546
TEMP B: 983 | 130 | 1420
对于 TEMP A、TEMP B中匹配区域以外出现的数码重复,要依据匹配区域内的位置逐一进行替换。匹配关系:1<——>5 3<——>6 7<——>0
子代A:802 | 567 | 9143
子代B:986 | 130 | 5427
(6)顺序交叉法(OX) (用于互换编码)
从父代A随机选一个编码子串,放到子代A的对应位置;子代A空余的位置从父代B中按B的顺序选取(与己有编码不重复)。同理可得子代B。
父代A: 872 | 139 | 0546
父代B: 983 | 567 | 1420
交叉后:
子代A: 856 | 139 | 7420
子代B: 821 | 567 | 3904
(7)循环交叉(CX)(用于互换编码)
CX同OX交叉都是从一个亲代中取一些城市,而其它城市来自另外一个亲代,但是二者不同之处在于:OX中来自第一个亲代的编码子串是随机产生的,而CX却不是,它是根据两个双亲相应位置的编码而确定的。
父代A:1 2 3 4 5 6 7 8 9
| | | | |
父代B:5 4 6 9 2 3 7 8 1
可得循环基因:1->5->2->4->9->1
用循环的基因构成子代A,顺序与父代A一样
1 2 4 5 9
用父代B剩余的基因填满子代A:
1 2 6 4 5 3 7 8 9
子代B的编码同理。(循环基因 5->1->9->4->2->5)
(8)两交换启发交叉(HGA)
两交换启发交叉方法的基本思想如下:
以8个城市的旅行商问题为例:设N个城市为1,2,3,4,5,6,7,8
随机选出一对未匹配的双亲如下:
A = 3 7 2 6 4 8 1 5
B = 4 8 3 2 1 7 5 6
随机选出初始城j=1(位置号),Sj=1(城市号),右转动使1成为两双亲的第一位置城市如下:
A1 = 1 5 3 7 2 6 4 8
B1 = 1 7 5 6 4 8 3 2
O1 = 1 × × × × × × ×
判断因为d(1,5)>d(1,7)则A1以7为中心右转得如下中间代:
A2 = × 7 2 6 4 8 5 3
B2 = × 7 5 6 4 8 3 2
O2 = 1 7 × × × × × ×
从第2位开始继续重复上述过程
判断因为d(7,5)=d(7,2)则可任选5或2,A2以5为中心右转得如下中间代:
A3 = × 7 5 3 2 6 4 8
B3 = × 7 5 6 4 8 3 2
O3 = 1 7 5 × × × × ×
如此反复得出
O = 1 7 5 3 2 6 4 8
(9)三交换启发交叉(THGA)(源代码中使用类似此方法)
三交换启发交叉方法的基本思想如下:
选3个参加交配的染色体作为父代,以8个城市为例来说明这一过程,其中dij由前面的表1给出,父代染色体为
A = 3 2 1 4 8 7 6 5
B = 2 4 6 8 1 3 5 7
C = 8 7 5 6 4 3 2 1
SUM1=42,SUM2=40,SUM3=46(SUM1,SUM2,SUM3分别为这3种排法所走的距离总和数).
随机选出初始城市j=1,Sj=3右转动,使3成为3父代的第1位置.
A = 3 2 1 4 8 7 6 5
B = 3 5 7 2 4 6 8 1
C = 3 2 1 8 7 5 6 4
由于d(3,2)>d(3,5),所以有:
A = × 5 2 1 4 8 7 6
B = × 5 7 2 4 6 8 1
C = × 5 6 4 2 1 8 7
由此规则计算可得:
O = 3 5 7 6 8 4 2 1
5、变异
变异是指依据变异概率将个体编码串中的某些基因值用其它基因值来替换,从而形成一个新的个体。GA中的变异运算是产生新个体的辅助方法,它决定了GA的局部搜索能力,同时保持种群的多样性。交叉运算和变异运算的相互配合,共同完成对搜索空间的全局搜索和局部搜索。
注:变异概率Pm不能太小,这样降低全局搜索能力;也不能太大,Pm > 0.5,这时GA退化为随机搜索。
(1)基本位变异算子(用于二进制编码)
基本位变异算子是指对个体编码串随机指定的某一位或某几位基因作变异运算。对于基本遗传算法中用二进制编码符号串所表示的个体,若需要进行变异操作的某一基因座上的原有基因值为0,则变异操作将其变为1;反之,若原有基因值为1,则变异操作将其变为0。
变异前:
000001110000000010000
变异后:
000001110001000010000
(2)逆转变异算子(用于互换编码)(源代码中使用类似此方法)
在个体中随机挑选两个逆转点,再将两个逆转点间的基因交换。
变异前:
1346798205
变异后:
1246798305
6、运行参数
GA运行时选择的参数应该视解决的具体问题而定,到目前为止,还没有一个适用于GA所有应用领域的关于算法参数的理论。下面是一般情况下使用GA时推荐的参数:
(1)交叉率
交叉率一般来说应该比较大,推荐使用80%-95%。
(2)变异率
变异率一般来说应该比较小,一般使用0.5%-1%最好。
(3)种群的规模
种群规模指的是群体中个体的个数。实验发现,比较大的种群的规模并不能优化遗传算法的结果。种群的大小推荐使用20-30,一些研究表明,种群规模 的大小取决于编码的方法,具体的说就是编码串(Encoded String)的大小。也就是说,如果说采用32位为基因编码的时候种群的规模大小最好为32的话,那么当采用16位为基因编码时种群的规模相应应变为原 来的两倍。
(4)遗传运算的终止进化代数
个人的想法是,设定一个计数器,如果连续N代出现的最优个体的适应度都一样时,(严格的说应该是,连续N代子代种群的最优个体适应度都<=父代最优个性的适应度)可以终止运算。也可以简单的根据经验固定进化的代数。
三、源代码如下,已加详细注释
- /*
- * 编写人:远航之帆
- * 时间:2011.8.26
- * 问题:旅行商问题
- * 算法:遗传算法
- * 作用:通过遗传算法计算一条最优路径并输出,该路经经历过以下地图的10个城市,并返回起始点,其中的这条路径长度最短或接近最短
- */
- #include "stdio.h"
- #include "string.h"
- #include "stdlib.h"
- #define city_num 10 //城市个数
- #define unit_num 50 //群体规模为50
- #define pc 0.9 //交叉概率为0.9
- #define pv 0.1 //变异概率为10%
- #define ps 0.6 //进行选择时保留的比例
- #define genmax 15 //最大代数15
- /* 定义个体信息 */
- typedef struct unit
- {
- int path[city_num]; //个体的路径信息
- int length; //个体代价值
- }Unit;
- typedef struct node
- {
- int city;
- struct node *next;
- }Node;
- Unit group[unit_num]; //种群变量group
- Unit bestone; //记录最短路径
- int generation_num=0; //记录当前达到第几代
- /***************************************************************************/
- /* 城市地图的距离信息: */
- /* 北京 天津 武汉 深圳 长沙 成都 杭州 西安 拉萨 南昌 */
- /* (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) */
- /* 北京(0) 0 1 1272 2567 1653 2097 1425 1177 3947 1 */
- /* 天津(1) 1 0 1 2511 1633 2077 1369 1157 3961 1518 */
- /* 武汉(2) 1272 1 0 1 380 1490 821 856 3660 385 */
- /* 深圳(3) 2567 2511 1 0 1 2335 1562 2165 3995 933 */
- /* 长沙(4) 1653 1633 380 1 0 1 1041 1135 3870 456 */
- /* 成都(5) 2097 2077 1490 2335 1 0 1 920 2170 1920 */
- /* 杭州(6) 1425 1369 821 1562 1041 1 0 1 4290 626 */
- /* 西安(7) 1177 1157 856 2165 1135 920 1 0 1 1290 */
- /* 拉萨(8) 3947 3961 3660 3995 3870 2170 4290 1 0 1 */
- /* 南昌(9) 1 1518 385 993 456 1920 626 1290 1 0 */
- /***************************************************************************/
- int length_table[10][10]={{0,1,1272,2567,1653,2097,1425,1177,3947,1},//城市地图映射表
- {1,0,1,2511,1633,2077,1369,1157,3961,1518},
- {1272,1,0,1,380,1490,821,856,3660,385},
- {2567,2511,1,0,1,2335,1562,2165,3995,933},
- {1653,1633,380,1,0,1,1041,1135,3870,456},
- {2097,2077,1490,2335,1,0,1,920,2170,1920},
- {1425,1369,821,1562,1041,1,0,1,4290,626},
- {1177,1157,856,2165,1135,920,1,0,1,1290},
- {3947,3961,3660,3995,3870,2170,4290,1,0,1},
- {1,1518,385,993,456,1920,626,1290,1,0}};
- /*****************************************************************************/
- /* */
- /* others */
- /* */
- /*****************************************************************************/
- /* 检查k是否在son[city_num]中已出现过 */
- Node *search_son(Node *p,int k)
- {
- while(p->next->city!=k)
- p=p->next;
- return p;
- }
- /* 将种群中个体按代价从小到大排序 */
- void Sort(Unit group[unit_num])
- {
- int i,j;
- Unit temp,*p1,*p2;
- for(j=1;j<=unit_num-1;j++) //排序总共需进行N-1轮
- {
- for(i=1;i<=unit_num-1;i++)
- {
- p1=&group[i-1];
- p2=&group[i];
- if(p1->length>p2->length) //总长度大的往后排
- {
- memcpy(&temp,p1,sizeof(Unit));
- memcpy(p1,p2,sizeof(Unit));
- memcpy(p2,&temp,sizeof(Unit));
- }//end if
- }//end 一轮排序
- }//end 排序
- if(group[0].length < bestone.length) //记录最优个体
- memcpy(&bestone,&group[0],sizeof(Unit));
- }
- /* 计算某个路径的总长度 */
- void Calculate_length(Unit *p)
- {
- int j;
- p->length=0;
- for(j=1;j<=city_num-1;j++)
- {
- p->length+=length_table[p->path[j-1]][p->path[j]];
- }
- p->length+=length_table[p->path[city_num-1]][p->path[0]];
- }
- /* 生成一个介于两整型数之间的随机整数 */
- int RandomInteger(int low,int high)
- {
- int rand_num;
- double d;
- d=(double)(rand()%100)/100.0; //d>0&&d<1
- rand_num=(int)(d*(high-low+1))+low;
- return rand_num;
- }
- /* 输出当代种群中的每个个体 */
- void Print_optimum(Unit group[unit_num],int k)
- {
- int i,j;
- Unit *p;
- printf("当前第 %d 代:\n",k);
- for(i=0;i<=unit_num-1;i++)
- {
- printf("第%2d代,个体%2d :",k,i);
- p=&group[i];
- for(j=0;j<=city_num-1;j++)
- printf("%d ",p->path[j]);
- printf(" 总路径长度为:%d \n",p->length);
- }
- }
- /* 输出最优个体 */
- void Print_bestone(Unit *bestone)
- {
- int i;
- Unit *p=bestone;
- printf("\n\n最优路径为:\n");
- for(i=0;i<=city_num-1;i++)
- printf("%d-->",p->path[i]);
- printf("%d 总路径长度为:%d \n",p->path[0],p->length);
- }
- /*****************************************************************************/
- /* */
- /* module */
- /* */
- /*****************************************************************************/
- /* 交叉 */
- void Cross_group(Unit *p1,Unit *p2,Unit *p3)
- {
- int i,j,k,Cross_group_point;
- int a,b,c;
- int son[city_num];
- Node *current1,*current2,*current3;
- Node *top1,*top2,*top3;
- Node *p;
- //将三个父代路径改为单循环链表
- top1=current1=(Node *)malloc(sizeof(Node)); //为第一个父代路径生成头一个�Y点
- top1->city=p1->path[0];
- top2=current2=(Node *)malloc(sizeof(Node)); //为第二个父代路径生成头一个�Y点
- top2->city=p2->path[0];
- top3=current3=(Node *)malloc(sizeof(Node)); //为第三个父代路径生成头一个�Y点
- top3->city=p3->path[0];
- for(i=1;i<city_num;i++) //生成三个父代路径的其他�Y点
- {
- current1->next=(Node *)malloc(sizeof(Node));
- current1=current1->next;
- current1->city=p1->path[i];
- current2->next=(Node *)malloc(sizeof(Node));
- current2=current2->next;
- current2->city=p2->path[i];
- current3->next=(Node *)malloc(sizeof(Node));
- current3=current3->next;
- current3->city=p3->path[i];
- }
- current1->next=top1; //链接第一个父代路径头尾结点
- current2->next=top2; //链接第二个父代路径头尾结点
- current3->next=top3; //链接第三个父代路径头尾结点
- Cross_group_point=RandomInteger(0,city_num-1); //三交换启发交叉
- while(Cross_group_point--)
- current1=current1->next;
- current2=search_son(top2,current1->next->city);
- current3=search_son(top3,current1->next->city);
- for(i=0;i<city_num;i++)
- {
- son[i]=current1->next->city; //将最优点存入son
- p=current1->next; //从第一个父代路径链表中删除该最优点
- current1->next=p->next;
- free(p);
- p=current2->next; //从第二个父代路径链表中删除该最优点
- current2->next=p->next;
- free(p);
- p=current3->next; //从第三个父代路径链表中删除该最优点
- current3->next=p->next;
- free(p);
- if(i==9)break;
- a=length_table[son[i]][current1->next->city];
- b=length_table[son[i]][current2->next->city];
- c=length_table[son[i]][current3->next->city];
- if(a<=b&&a<=c){ //比较最短踞离后,将三条父代路径链表定位于最优点的前一个节点
- current2=search_son(current2,current1->next->city);
- current3=search_son(current3,current1->next->city);
- }
- else if(b<=a&&b<=c){
- current1=search_son(current1,current2->next->city);
- current3=search_son(current3,current2->next->city);
- }
- else if(c<=a&&c<=b){
- current1=search_son(current1,current3->next->city);
- current2=search_son(current2,current3->next->city);
- }
- }
- memcpy(p1->path,son,sizeof(p1->path)); //生成第一个子代路径
- Cross_group_point=RandomInteger(0,city_num-1); //生成第二个子代路径
- for(k=0,i=Cross_group_point;i<city_num;i++)
- p2->path[k++]=son[i];
- for(i=0;i<Cross_group_point;i++)
- p2->path[k++]=son[i];
- Cross_group_point=RandomInteger(0,city_num-1); //生成第三个子代路径
- for(k=0,i=Cross_group_point;i<city_num;i++)
- p3->path[k++]=son[i];
- for(i=0;i<Cross_group_point;i++)
- p3->path[k++]=son[i];
- Calculate_length(p1); //计算子代p1路径的总长度
- Calculate_length(p2); //计算子代p2路径的总长度
- Calculate_length(p3); //计算子代p3路径的总长度
- }
- /* 变异 */
- void Varation_group(Unit *group,int gen_num)
- {
- int flag,i,j,k,temp;
- Unit *p;
- flag=(gen_num>50)?(3*100*pv):(100*pv); //在进化后期,增大变异概率
- while(flag--)
- {
- i=RandomInteger(0,unit_num-1); //确定发生变异的个体
- j=RandomInteger(0,city_num-1); //确定发生变异的位
- k=RandomInteger(0,city_num-1);
- p=&group[i]; //变异
- temp=p->path[j];
- p->path[j]=p->path[k];
- p->path[k]=temp;
- Calculate_length(p); //重新计算变异后路径的总长度
- }
- }
- /* 初始化最优值 */
- void Initial_bestone(Unit *bestone)
- {
- bestone->length=RAND_MAX;
- }
- /* 初始化种群 */
- void Initial_group(Unit *group)
- {
- int i,j,k;
- Unit *p;
- for(i=0;i<=unit_num-1;i++) //初始化种群里的100个个体
- {
- p=group+i; //p指向种群的第i个个体
- for(j=0;j<=city_num-1;j++) //初始化每个个体的路径
- {
- k=0;
- if(j==0) p->path[j]=RandomInteger(0,city_num-1);
- else
- {
- p->path[j]=RandomInteger(0,city_num-1);
- while(k<j)
- { //与之前城市重复,重新生成一个城市
- if(p->path[j]==p->path[k])
- {
- p->path[j]=RandomInteger(0,city_num-1);
- k=0;
- }
- else k++;
- }//end while
- }
- }//end for //初始化路径
- Calculate_length(p); //计算该路径的总长度
- }//end for //初始化种群
- }
- /* 进化种群 */
- void Evolution_group(Unit *group)
- {
- int i,j;
- int temp1,temp2;
- temp1=unit_num*(1-ps);
- temp2=unit_num*ps;
- for(i=1;i<=genmax;i++)
- {
- //选择
- Sort(group);
- Print_optimum(group,i-1); //输出当代(第i-1代)种群
- for(j=0;j<=temp1-1;j++)
- memcpy(&group[j+temp2],&group[j],sizeof(Unit));
- //交叉
- for(j=0;j<unit_num-2;)
- {
- Cross_group(&group[j],&group[j+1],&group[j+2]);
- j+=3;
- }
- //变异
- Varation_group(group,i);
- }
- Sort(group);
- Print_optimum(group,i-1); //输出当代(第i-1代)种群
- }
- /*主函数*/
- int main()
- {
- srand((int)time(NULL)); //初始化随机数发生器
- Initial_bestone(&bestone); //初始化最优值
- Initial_group(group); //初始化种群
- Evolution_group(group); //种群进化:选择、交叉、变异
- Print_bestone(&bestone);
- return 0;
- }
本文出自 “Linuxer’s Blog” 博客,谢绝转载!