谈谈计算机和网络常用进位制:二进制(Binary)、十进制(Decimal)和十六进制(He
谈谈计算机和网络常用进位制:二进制(Binary)、十进制(Decimal)和十六进制(Hexadecimal)
二进制、十进制和十六进制,这几个个进制里算十进制我们最熟悉了,从学前教育或者幼儿园最先接触的数学到再我们日常生活几乎天天和他打交道的下面这十个数字。

但是,话又说回来,你真的理解这10个数字吗?或者说你理解十进制吗?
今天我们就以十进制为切入点顺便谈谈二进制、十六进制以及它们之间的转换。在谈这些进制之前我们先了解一下进制的概念:
所谓进制就是进位制,是人们规定的一种进位方法。进位制/位置计数法是一种记数方式,故亦称进位记数法/位值计数法,可以用有限的数字符号代表所有的数值。可使用数字符号的数目称为基数或底数(radix),基数为n,即可称n进位制,简称n进制。
对于任何一种进位制---n进制,就表示某一位置上的数运算时是逢“n”自右至左进一位。 十进制是逢“十”进一,十六进制是逢“十六”进一,“二”进制就是逢二进一,以此类推,n进制就是逢n进位。现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数。
注意:十进制是0-9十个数值进行记数,而不是1-10,其他进制也同样n进制就是用0--(n-1)的数字进行记数而不是0-n。
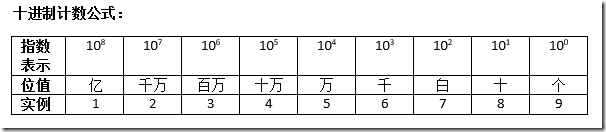
计数值:等于把上面的各个单元格的值乘以单元格实例的值最后再把所有单元格乘出的值相加。
以上面的实例的值为例:1X亿 + 2X千万 + 3X百万 + 4X十万 + 5X万 + 6X千 + 7X白 + 8X十 + 9X1=123456789.
十进制非常容易理解,因为我们从小就接触它,所以对它非常熟悉。假如突然让你转到二进制计数法,而且日常生活都用二进制计数的话,会出现什么情况?答案是你几乎会疯掉,因为二进制一般是让电脑去理解并使用它的而不是为我们的日常生活中使用它而设计的,因为二进制只有两个数值0和1进行计数,如果一个庞大的数字用二进制表示的话,那么会是一窜很长的数字。如11011011这让你看起来像个符文,而不能马上说出它的值,然而电脑却不然,它更喜欢读取使用这种“符文”。
其实在学网络的时候特别是接触IP地址的时候,你需要真正明白二进制以及二进制和十进制、十六进制之间的转换,这是很重要的。下面就开始介绍二进制,它非常简单,二进制只使用数字0和1,其中每个数值对应一位(二进制位),二进制位按从右向左的顺序排列,每向左移动一位,位值就翻一倍。通常我们将每4位或者八位作为一组,分别称它们为半字节(nibble)和字节(Byte)。

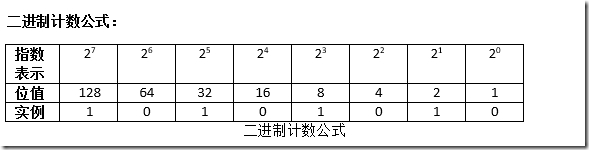
计数值:等于把上面的各个单元格的值乘以实单元格实例的值最后再把所有单元格乘出的值相加。
以上面的实例的值为例:1X128 + 0X64 + 1X32 + 0X16 + 1X8 + 0X4 + 1X2 + 0X1=
128+0+32+0+8+0+2+0=170
二进制和十进制之间的转换
上面已经介绍了十进制和二进制,下面就介绍他们之间如何转换。下表列出了半字节和字节中各位代表的十进制值。
半字节中各位的位值 |
字节中各位的位值 |
8 4 2 1 |
128 64 32 16 8 4 2 1 |
这意味着,如果某一位的值取值为1,则计算半字节或者字节对应的十进制值时,应将其位值与其所有取值为1的位值相加。如果为0则不考虑。
如果半字节的每一位都为1,则将8、4、2和1相加,结果为15―半字节的最大取值。假设半字节的取值为1010,即对应位为1的位值为8和2,则对应的十进制值为8+2=10.
同理,字节的转换方法和半字节一样,但是字节的取值要比半字节的最大取值15大得多,如果字节的每位都为1,则其取值如下(字节有8个位):
128+64+32=16+8+4+2+1=255。
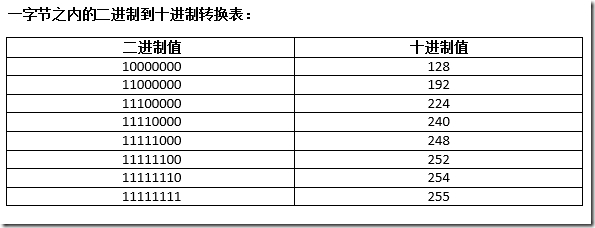
十进制到二进制的转换就是上面方法的相反过程,方法如下:
1. 先取和该十进制值最接近的并且小于该十进制大小的一个二进制位值。
2. 用十进制值减去刚刚的接近值,得出的差。
3. 按照第一、二步接着取第二个,第三个以此类推。
4. 得到差为0.
5. 把所有位值并所得的结果进行“或”运算,运算的结果就是对应的二进制值。
下面用一个实例来说明:
如十进制234转换为二进制。
和234最接近大小的二进制位值为224(11100000)
234-224=10
和10最接近的二进制位值为8(00001000)
10-8=2(00000010)
对上面的二进制进行与运算:
11100000
00001000
00000100
11101100
十六进制和二进制、十进制之间的转换
十六进制与二进制和十进制完全不同,我们通过读取半字节将二进制转换为十六进制。为什么呢?因为一个半字节刚好满足一个十六进制的最大值15。即半字节的所有位都取1。
1111,十进制值为8+4+2+1=15。十进制使用0―9十个数字而十六进制除了使用十进制的十个数字外另外6个用啥代替呢?10、11、12、13、14、15吗?那可不行,因为10―15这6个数字不是二位数,因此我们使用A、B、C、D、E、F来代表10、11、12、13、14、15。
每个十六进制字符相当于半字节,而两个十六进制字符就相当于一字节。要计算该十六进制数对应的二进制值,即可将这两个十六进制字符分别转为二进制的半字节,然后将他们合并为一个字节即可。下面用几个实例介绍一下十六进制和二进制、十进制之间的转换方法:
实例1、十六进制0x7B(一般以0x前缀代表后面的数十十六进制)转为二进制和十进制。
转为二进制:
上面讲过,十六进制的每个字符 为半个字节,我们分别来拆开来看:7=0111而B=1011,因此整个字节为01111011。
转为十进制:
7 X (16)1 + B X (16)0 = 112 + 11 = 123。
实例2、二进制10110101转换为十六进制和十进制。
转为十六进制:
先把10110101字节拆为两个字节:1011和0101。1011对应的十六进制字符为B(8+0+2+1),0101对应的十六进制字符为5(0+4+0+1),所以十六进制的值为0xB5。
转换为十进制:
128 + 32 + 16 + 4 + 1 = 181
其实对于任何一个数,我们可以用不同的进位制来表示。比如:十进数57(10),可以用二进制表示为00111001(2),也可以用五进制表示为212(5),也可以用八进制表示为71(8)用十六进制表示为39(16),它们所代表的数值都是一样的,只是我们日常生活中习惯于用十进制来表示而计算机常用二进制和十六进制来表示而已!
好了,本篇文章就到此结束,希望给刚接触计算机或者网络领域的朋友能有个好的开始!