“chaos算法”--之平衡二叉树

　   平衡二叉树（Balanced Binary Tree）是二叉查找树的一个进化体，也是第一个引入平衡概念的二叉树。1962年，G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树，所以它又叫AVL树。平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

　　平衡二叉树实现的大部分过程和二叉查找树是一样的（学平衡二叉树之前一定要会二叉查找树），区别就在于插入和删除之后要写一个旋转算法去维持平衡，维持平衡需要借助一个节点高度的属性。我参考了机械工业出版社的《数据结构与算法分析-C语言描述》写了一个C++版的代码。这本书的AVLTree讲的很好，不过没有很完整的去描述。我会一步一步的讲解如何写平衡二叉树，重点是平衡二叉树的核心部分，也就是旋转算法。

第一步：节点信息

　　相对于二叉查找树的节点来说，我们需要用一个属性二叉树的高度，目的是维护插入和删除过程中的旋转算法。

代码如下：

// AVL树节点信息
template< class T>
class TreeNode
{
public:
       TreeNode():lson(NULL),rson(NULL),freq(1),hgt(0){}
       T data; // 值
int hgt; // 以此节点为根的树的高度
       unsigned int freq; // 频率
       TreeNode* lson; // 指向左儿子的地址
       TreeNode* rson; // 指向右儿子的地址
};

第二步：平衡二叉树类的声明

　　声明中的旋转函数将在后边的步骤中详解。

代码如下：

// AVL树类的属性和方法声明
template< class T>
class AVLTree
{
private:
       TreeNode<T>* root; // 根节点
void insertpri(TreeNode<T>* &node,T x); // 插入
       TreeNode<T>* findpri(TreeNode<T>* node,T x); // 查找
void insubtree(TreeNode<T>* node); // 中序遍历
void Deletepri(TreeNode<T>* &node,T x); // 删除
int height(TreeNode<T>* node); // 求树的高度
void SingRotateLeft(TreeNode<T>* &k2); // 左左情况下的旋转
void SingRotateRight(TreeNode<T>* &k2); // 右右情况下的旋转
void DoubleRotateLR(TreeNode<T>* &k3); // 左右情况下的旋转
void DoubleRotateRL(TreeNode<T>* &k3); // 右左情况下的旋转
int Max( int cmpa, int cmpb); // 求最大值

public:
       AVLTree():root(NULL){}
void insert(T x); // 插入接口
       TreeNode<T>* find(T x); // 查找接口
void Delete(T x); // 删除接口
void traversal(); // 遍历接口

};

第三步：两个辅助方法

　　旋转算法需要借助于两个功能的辅助，一个是求树的高度，一个是求两个高度的最大值。这里规定，一棵空树的高度为-1，只有一个根节点的树的高度为0，以后每多一层高度加1。为了解决指针NULL这种情况，写了一个求高度的函数，这个函数还是很有必要的。

代码如下：

// 计算以节点为根的树的高度
template< class T>
int AVLTree<T>::height(TreeNode<T>* node)
{
if(node!=NULL)
return node->hgt;
return -1;
}
// 求最大值
template< class T>
int AVLTree<T>::Max( int cmpa, int cmpb)
{
return cmpa>cmpb?cmpa:cmpb;
}

第四步：旋转

　　对于一个平衡的节点，由于任意节点最多有两个儿子，因此高度不平衡时，此节点的两颗子树的高度差2.容易看出，这种不平衡出现在下面四种情况：

　1、6节点的左子树3节点高度比右子树7节点大2，左子树3节点的左子树1节点高度大于右子树4节点，这种情况成为左左。

　2、6节点的左子树2节点高度比右子树7节点大2，左子树2节点的左子树1节点高度小于右子树4节点，这种情况成为左右。

　3、2节点的左子树1节点高度比右子树5节点小2，右子树5节点的左子树3节点高度大于右子树6节点，这种情况成为右左。

　4、2节点的左子树1节点高度比右子树4节点小2，右子树4节点的左子树3节点高度小于右子树6节点，这种情况成为右右。

　　从图2中可以可以看出，1和4两种情况是对称的，这两种情况的旋转算法是一致的，只需要经过一次旋转就可以达到目标，我们称之为单旋转。2和3两种情况也是对称的，这两种情况的旋转算法也是一致的，需要进行两次旋转，我们称之为双旋转。

第五步：单旋转

　　单旋转是针对于左左和右右这两种情况的解决方案，这两种情况是对称的，只要解决了左左这种情况，右右就很好办了。图3是左左情况的解决方案，节点k2不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的左子树X子树，所以属于左左情况。

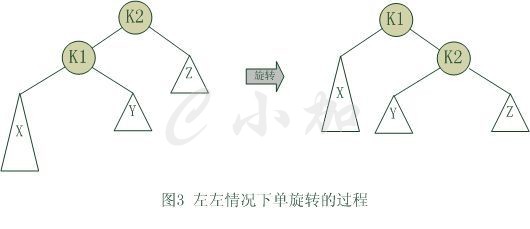
　　为使树恢复平衡，我们把k2变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质。

　　这样的操作只需要一部分指针改变，结果我们得到另外一颗二叉查找树，它是一棵AVL树，因为X向上一移动了一层，Y还停留在原来的层面上，Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同，插入操作使得X高度长高了。因此，由于这颗子树高度没有变化，所以通往根节点的路径就不需要继续旋转了。

代码如下：

// 左左情况下的旋转
template< class T>
void AVLTree<T>::SingRotateLeft(TreeNode<T>* &k2)
{
   TreeNode<T>* k1;
   k1=k2->lson;
   k2->lson=k1->rson;
   k1->rson=k2;

   k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
   k1->hgt=Max(height(k1->lson),k2->hgt)+1;
}
// 右右情况下的旋转
template< class T>
void AVLTree<T>::SingRotateRight(TreeNode<T>* &k2)
{
   TreeNode<T>* k1;
   k1=k2->rson;
   k2->rson=k1->lson;
   k1->lson=k2;

   k2->hgt=Max(height(k2->lson),height(k2->rson))+1;
   k1->hgt=Max(height(k1->rson),k2->hgt)+1;
}

第六步：双旋转

　　对于左右和右左这两种情况，单旋转不能使它达到一个平衡状态，要经过两次旋转。双旋转是针对于这两种情况的解决方案，同样的，这样两种情况也是对称的，只要解决了左右这种情况，右左就很好办了。图4是左右情况的解决方案，节点k3不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的右子树k2子树，所以属于左右情况。

　　为使树恢复平衡，我们需要进行两步，第一步，把k1作为根，进行一次右右旋转，旋转之后就变成了左左情况，所以第二步再进行一次左左旋转，最后得到了一棵以k2为根的平衡二叉树树。

代码如下：

// 左右情况的旋转
template< class T>
void AVLTree<T>::DoubleRotateLR(TreeNode<T>* &k3)
{
   SingRotateRight(k3->lson);
   SingRotateLeft(k3);
}
// 右左情况的旋转
template< class T>
void AVLTree<T>::DoubleRotateRL(TreeNode<T>* &k3)
{
   SingRotateLeft(k3->rson);
   SingRotateRight(k3);
}

第七步：插入

　　插入的方法和二叉查找树基本一样，区别是，插入完成后需要从插入的节点开始维护一个到根节点的路径，每经过一个节点都要维持树的平衡。维持树的平衡要根据高度差的特点选择不同的旋转算法。

代码如下：

// 插入
template< class T>
void AVLTree<T>::insertpri(TreeNode<T>* &node,T x)
{
if(node==NULL) // 如果节点为空,就在此节点处加入x信息
   {
       node= new TreeNode<T>();
       node->data=x;
return;
   }
if(node->data>x) // 如果x小于节点的值,就继续在节点的左子树中插入x
   {
       insertpri(node->lson,x);
if(2==height(node->lson)-height(node->rson))
if(x<node->lson->data)
               SingRotateLeft(node);
else
               DoubleRotateLR(node);
   }
else if(node->data<x) // 如果x大于节点的值,就继续在节点的右子树中插入x
   {
       insertpri(node->rson,x);
if(2==height(node->rson)-height(node->lson)) // 如果高度之差为2的话就失去了平衡,需要旋转
if(x>node->rson->data)
               SingRotateRight(node);
else
               DoubleRotateRL(node);
   }
else ++(node->freq); // 如果相等,就把频率加1
   node->hgt=Max(height(node->lson),height(node->rson));
}
// 插入接口
template< class T>
void AVLTree<T>::insert(T x)
{
   insertpri(root,x);
}

第八步：查找

和二叉查找树相比，查找方法没有变法，不过根据存储的特性，AVL树能维持在一个O(logN)的稳定的时间，而二叉查找树则相当不稳定。

代码如下：

// 查找
template< class T>
TreeNode<T>* AVLTree<T>::findpri(TreeNode<T>* node,T x)
{
if(node==NULL) // 如果节点为空说明没找到,返回NULL
   {
return NULL;
   }
if(node->data>x) // 如果x小于节点的值,就继续在节点的左子树中查找x
   {
return findpri(node->lson,x);
   }
else if(node->data<x) // 如果x大于节点的值,就继续在节点的左子树中查找x
   {
return findpri(node->rson,x);
   }
else return node; // 如果相等,就找到了此节点
}
// 查找接口
template< class T>
TreeNode<T>* AVLTree<T>::find(T x)
{
return findpri(root,x);
}

第九步：删除

　　删除的方法也和二叉查找树的一致，区别是，删除完成后，需要从删除节点的父亲开始向上维护树的平衡一直到根节点。

代码如下：

// 删除
template< class T>
void AVLTree<T>::Deletepri(TreeNode<T>* &node,T x)
{
if(node==NULL) return ; // 没有找到值是x的节点
if(x < node->data)
   {
        Deletepri(node->lson,x); // 如果x小于节点的值,就继续在节点的左子树中删除x
if(2==height(node->rson)-height(node->lson))
if(node->rson->lson!=NULL&&(height(node->rson->lson)>height(node->rson->rson)) )
               DoubleRotateRL(node);
else
               SingRotateRight(node);
   }

else if(x > node->data)
   {
        Deletepri(node->rson,x); // 如果x大于节点的值,就继续在节点的右子树中删除x
if(2==height(node->lson)-height(node->rson))
if(node->lson->rson!=NULL&& (height(node->lson->rson)>height(node->lson->lson) ))
               DoubleRotateLR(node);
else
               SingRotateLeft(node);
   }

else // 如果相等,此节点就是要删除的节点
   {
if(node->lson&&node->rson) // 此节点有两个儿子
       {
           TreeNode<T>* temp=node->rson; // temp指向节点的右儿子
while(temp->lson!=NULL) temp=temp->lson; // 找到右子树中值最小的节点
// 把右子树中最小节点的值赋值给本节点
           node->data=temp->data;
           node->freq=temp->freq;
           Deletepri(node->rson,temp->data); // 删除右子树中最小值的节点
if(2==height(node->lson)-height(node->rson))
           {
if(node->lson->rson!=NULL&& (height(node->lson->rson)>height(node->lson->lson) ))
                   DoubleRotateLR(node);
else
                   SingRotateLeft(node);
           }
       }
else // 此节点有1个或0个儿子
       {
           TreeNode<T>* temp=node;
if(node->lson==NULL) // 有右儿子或者没有儿子
           node=node->rson;
else if(node->rson==NULL) // 有左儿子
           node=node->lson;
           delete(temp);
           temp=NULL;
       }
   }
if(node==NULL) return;
   node->hgt=Max(height(node->lson),height(node->rson))+1;
return;
}
// 删除接口
template< class T>
void AVLTree<T>::Delete(T x)
{
   Deletepri(root,x);
}

第十步：中序遍历

代码如下：

// 中序遍历函数
template< class T>
void AVLTree<T>::insubtree(TreeNode<T>* node)
{
if(node==NULL) return;
   insubtree(node->lson); // 先遍历左子树
   cout<<node->data<<" "; // 输出根节点
   insubtree(node->rson); // 再遍历右子树
}
// 中序遍历接口
template< class T>
void AVLTree<T>::traversal()
{
   insubtree(root);
}

第十一步：关于效率

此数据结构插入、查找和删除的时间复杂度均为O(logN)，但是插入和删除需要额外的旋转算法需要的时间，有时旋转过多也会影响效率。

　　关于递归和非递归。我用的是递归的方法进行插入，查找和删除，而非递归的方法一般来说要比递归的方法快很多，但是我感觉非递归的方法写出来会比较困难，所以我还是选择了递归的方法。

　　还有一种效率的问题是关于高度信息的存储，由于我们需要的仅仅是高度的差，不需要知道这棵树的高度，所以只需要使用两个二进制位就可以表示这个差。这样可以避免平衡因子的重复计算，可以稍微的加快一些速度，不过代码也丧失了相对简明性和清晰度。如果采用递归写法的话，这种微加速就更显得微乎其微了。

　　如果有哪些不对的或者不清晰的地方请指出，我会修改并加以完善。

转载自：http://www.cppblog.com/cxiaojia/archive/2012/08/20/187776.html