MTBF
MTBF
MTBF(Mean Time Between Failure,平均故障间隔时间)
目录[隐藏]
|
MTBF概述
MTBF,平均故障间隔时间又称平均无故障时间,英文全称是“Mean Time Between Failures”指可修复产品两次相邻故障之间的平均时间,记为MTBF。MTBF是衡量一个产品(尤其是电器产品)的可靠性指标。单位为“小时”。它反映了产品的时间质量,是体现产品在规定时间内保持功能的一种能力。具体来说,它仅适用于可维修产品。同时也规定产品在总的使用阶段累计工作时间与故障次数的比值为MTBF。磁盘阵列产品一般MTBF不能低于50000小时。
随着伺服器的广泛应用,对伺服器的可靠性提出了更高的要求。所谓“可靠性”,就是产品在规定条件下和规定时间内完成规定功能的能力;反之,产品或其一部分不能或将不能完成规定的功能是出故障。概括地说,产品故障少的就是可靠性高,产品的故障总数与寿命单位总数之比叫“故障率”(Failure rate),常用λ表示。例如正在运行中的100只硬碟,一年之内出了2次故障,则每个硬碟的故障率为0.02次/年。当产品的寿命服从指数分布时,其故障率的倒数就叫做平均故障间隔时间(Mean Time Between Failures),简称MTBF。
MTBF的计算
设有一个可修复的产品在使用过程中,共计发生过N0次故障,每次故障后经过修复又和新的一样继续投入使用,其工作时间分别为: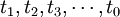 ,那么产品的平均故障间隔时间,也就是平均寿命为Q为:
,那么产品的平均故障间隔时间,也就是平均寿命为Q为:
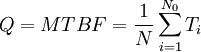
通常,我们在产品的手册或包装上能够看到这个MTBF值,如8000小时,2万小时,那么,MTBF的数值是怎样算出来的呢,假设一台电脑的MTBF 为3万小时,是不是把这台电脑连续运行3万小时检测出来的呢?答案是否定的,如果是那样的话,我们有那么多产品要用几十年都检测不完的。其实,关于 MTBF值的计算方法,目前最通用的权威性标准是MIL-HDBK-217、GJB/Z299B和Bellcore,分别用于军工产品和民用产品。其中,MIL-HDBK-217是由美国国防部可靠性分析中心及Rome实验室提出并成为行业标准,专门用于军工产品MTBF值计算,GJB/Z299B是我国军用标准;而Bellcore是由AT&TBell实验室提出并成为商用电子产品MTBF值计算的行业标准。
MTBF计算中主要考虑的是产品中每个器件的失效率。但由于器件在不同的环境、不同的使用条件下其失效率会有很大的区别,例如,同一产品在不同的环境下,如在实验室和海洋平台上,其可靠性值肯定是不同的;又如一个额定电压为16V的电容在实际电压为25V和5V下的失效率肯定是不同的。所以,在计算可靠性指标时,必须考虑上述多种因素。所有上述这些因素,几乎无法通过人工进行计算,但借助于软件如MTBFcal软件和其庞大的参数库,我们就能够轻松的得出MTBF值。
MTTF、MTBF和MTTR的区别
可靠性是最初是确定一个系统在一个特定的运行时间内有效运行的概率的一个标准。可靠性的衡量需要系统在某段时间内保持正常的运行。
目前,使用最为广泛的一个衡量可靠性的参数是,MTTF(mean time to failure,平均失效前时间),定义为随机变量、出错时间等的"期望值"。但是,MTTF经常被错误地理解为,"能保证的最短的生命周期"。MTTF 的长短,通常与使用周期中的产品有关,其中不包括老化失效。
MTTR(mean time to restoration,平均恢复前时间),源自于IEC 61508中的平均维护时间(mean time to repair),目的是为了清楚界定术语中的时间的概念,MTTR是随机变量恢复时间得期望值。它包括确认失效发生所必需的时间,以及维护所需要的时间。 MTTR也必须包含获得配件的时间,维修团队的响应时间,记录所有任务的时间,还有将设备重新投入使用的时间。
MTBF(Mean time between failures,平均故障间隔时间)定义为,失效或维护中所需要的平均时间,包括故障时间以及检测和维护设备的时间。对于一个简单的可维护的元件,MTBF = MTTF + MTTR。因为MTTR通常远小于MTTF,所以MTBF近似等于MTTF,通常由MTTF替代。MTBF用于可维护性和不可维护的系统。
MTBF分析的目的[1]
1)针对高频率故障零件的重点对策及零件寿命延长的技术改造依据。
2)进行零件寿命周期的推算及最佳维修计划编制。
3)有关点检对象、项目的选择与点检基准的设定、改善。
4)用于指导内外部维修工作分配。根据公司内设备修复能力的评价,以设备类型、作业种类的不同来决定内部分别承担工作的维修质量与设备效率方面的风险,作为维修外包的重要参考。
5)设定备品备件基准。机械、电气零件的各储备项目及基本库存数量,应根据MTBF的记录分析来判断,使其库存水平达到最经济的状况。
6)作为选择维修技术方法改善重点的参考依据。为了提高设备开动率,必须缩短与设备停机相关的长时间维修作业及工程调整、切换的时间。因此,有必要对维护作业方法进行检验,而其检验的项目、优先顺序的选择等基本情况,均需要依据MTBF的分析记录表。
7)用于设备对象设定预估运行时间标准,及其维护作业的选定与维护时间标准的研究。维修计划预估时间标准的设定及维护作业的选定,必须考虑设备维护重复周期或标准时间值与实际维护时间的差异及相应维护作业特性等因素,因此,MTBF分析表是非常必要的。
8)图样整理及重新选定重点设备或零件时的参考。MTBF的分析记录表所记录的设备零件改造项目或摩擦劣化等信息,以及设备图样修改或前期制作等情况,通过能经常作分析检验及重要性排序管理,可以使工程图样管理变得更容易。
9)运行操作标准的设定、修订及决定设备维护业务的责任分派。
10)提供设备的可靠性、可维修性设计的技术资料。维护技术最重要的是以MTBF分析表为基础,收集有关设备的可靠性、可维修性设计的技术信息,以便提供给设计部门在设计设备时参考。
MTBF分析的应用[1]
1)对于维修部门而言,很难了解维修活动与产品质量间的关系。例如,就故障修理而言,一般多以功能修理为重点,不会去确认维修作业所达到的产品质量改善的情况。但如何将产品质量和维修活动相结合,是非常重要的,MTBF分析表可作为重要的参考资料。
2)PM(生产维修)是着重以设备诊断技术为中心的预知维修,但其具体课题结果是很难把握的;从MTBF分析表中,找出设备诊断技术开发的课题,是一种很有效果的做法。
3)设备培训资料的制作:培养对设备熟悉、能力强的人员是PM的重要课题,然而一般培训多以市面上销售书籍为范本,并没有充分结合自己公司、单位的问题状况,与书本上所述的背景问更存在着差异。因此,如果能利用MTBF分析,培训有关公司生产设备的结构、功能、薄弱环节及注意事项,是较具体的做法。
4)关于设备寿命周期费用(LifeCycleCost,LCC)的把握及其研究资料:MTBF分析表,是以设备为主体,经长期而编制的一览表。因此,根据设备所发生的维修作业、费用、备品备件及损失的发生状况,来掌握设备寿命周期费用资料,是设备一生管理的重要基础。综上所述,MTBF分析不仅是维修记录的方法之一,其维修记录更可作为维护活动、管理和技术活动指南的原始资料,价值和意义重大。
制作MTBF分析表的注意事项[1]
1)应具备一览性,尽可能将相关资料整理在一张表上,不要散乱。
2)将一特定期间内的维修数据及相关资料,按照时间序列进行整理、记录,以便于了解。
3)可同时进行维修的记录和分析。
4)多花点心思,在一张表内整理多种信息:不仅可以将设备故障或维修资料记录下来,还可将质量、安全、成本等信息整理成与制造、设计、技术相关的参考资料。
5)通过MTBF分析表即可了解设备管理的重点。
6)通过MTBF分析表可判断故障和维护的关系。
7)了解改善对策及对策实施后的效果。
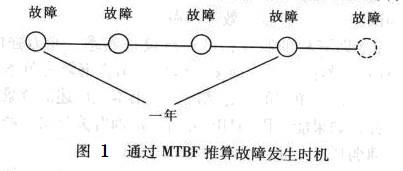
8)应使任何人都可容易进行资料的记录。例如在一年设备开动期间曾发生4次故障,则平均故障间隔时间为3个月。以【图1】为例,可以推算出每3个月将会发生一次故障。另外,也可依照这些故障点的分布状况,推断下次可能发生故障的设备部位及零件。
MTBF分析表制作的五个步骤[1]
步骤1:确定要分析的设备对象――通常先选择重点设备来记录,也可以按某类设备群或针对设备某重点部位进行记录。
步骤2:故障资料的收集――以过去3~5年或至少30次以上的设备故障资料来分析。
步骤3:故障分布图的绘制――将设备整体示意图绘出,利用步骤2的资料,标示出故障部位,如【图2】所示。

步骤4:编制MTBF分析表(如【图3】所示)。
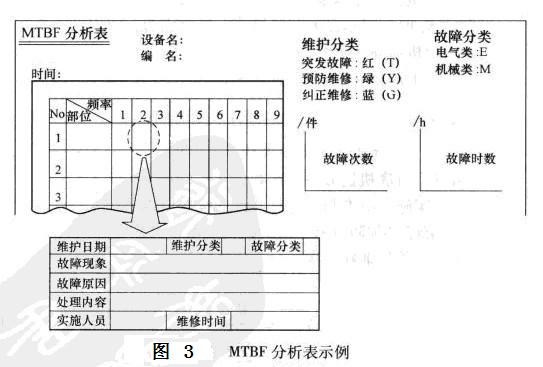
・分析表的内容以能记入一年的资料为准。
・将步骤3的内容,按部位类别、发生日期顺序记录。
・尽可能用图形方式或颜色类别、记号记录,以增加易读性。
・持续记录到“设备突发故障为零时”为止。
步骤5:故障分析及对策的检验。
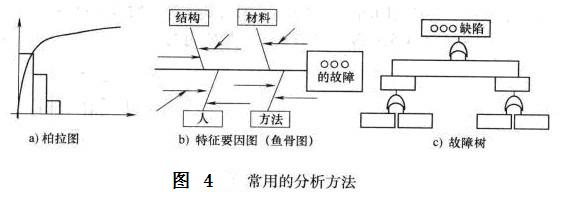
・由MTBF分析表来做故障原因分析及对策检验(常用的分析方法包括柏拉图、特征要因图(鱼骨图)和故障树法等,如【图4】所示)。
・对策方法应采用易懂的方式,并切实可行。
MTBF的案例分析
案例一:MTBF分布模型的案例分析[2]
考核机电产品的可靠性水平通常用平均故障间隔时间(MTBF)来衡量,即:考核产品在规定条件下和规定时间内,完成规定功能的能力。根据考核结果(MTBF)的值,判断该产品目前在国内外同类产品中所处地位,对于可靠性水平较低的产品,提出相应改进措施,切实提高产品可靠性。归根结底要对MTBF进行分析。
下面以某数控机床厂生产的系列加工中心为例,通过对采用定时截尾的方法对6台同系列不同编号的加工中心现场使用情况所收集的共30条数据进行分析,根据故障观测值的分布形状来拟合已知线形,应用数理统计中的参数估计、假设检验等方法进行验证,从而判断出故障间隔时间的分布模型,为进行故障分析、预测及实现可靠性增长提供了理论依据。
- 1 故障间隔时间分布模型的初步判断
- 1. 1 概率密度的观测值
下面由该系列加工中心故障间隔时间的观测值来拟合其概率密度函数。将故障间隔时间的观测值t∈[7.06, 1494.51]分为13组,如表1所示。
表1 TH42系列加工中心故障频率
Table 1
| 组号 | 区间上 | 区间下 | 组中值 | 频数 | 频率 | 累计 |
| 1 | 7.06 | 121.48 | 64.27 | 4 | 0.1333 | 0.1333 |
| 2 | 121.48 | 235.9 | 178.69 | 3 | 0.1 | 0.2333 |
| 3 | 235.9 | 350.32 | 293.11 | 4 | 0.1333 | 0.3667 |
| 4 | 350.32 | 464.74 | 407.53 | 4 | 0.1333 | 0.5 |
| 5 | 464.74 | 579.16 | 521.95 | 5 | 0.1667 | 0.6667 |
| 6 | 579.16 | 693.58 | 636.37 | 1 | 0.0333 | 0.7 |
| 7 | 693.58 | 807.99 | 750.79 | 4 | 0.1333 | 0.8333 |
| 8 | 807.99 | 922.41 | 865.2 | 2 | 0.0667 | 0.9 |
| 9 | 922.41 | 1036.83 | 979.62 | 0 | 0 | 0.9 |
| 10 | 1036.83 | 1151.25 | 1094.04 | 0 | 0 | 0.9 |
| 11 | 1151.25 | 1265.67 | 1208.46 | 1 | 0.0333 | 0.9333 |
| 12 | 1265.67 | 1380.09 | 1322.88 | 1 | 0.0333 | 0.9667 |
| 13 | 1380.09 | 1494.51 | 1437.3 | 1 | 0.0333 | 1 |
 以每组时间的中值为横坐标,每组的概率密度的观测值f(t)为纵坐标,f(t)的计算如下:
以每组时间的中值为横坐标,每组的概率密度的观测值f(t)为纵坐标,f(t)的计算如下:
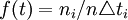 (1)
(1)
式中:ni―――每组故障间隔时间中的故障频数;
n―――早期故障总频数,本试验为30次;
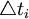 ―――组距,为114.42h。
―――组距,为114.42h。
由此拟合出的概率密度函数的曲线如图5所示。
由概率论可知,故障间隔时间的概率密度曲线呈单调下降趋势。可见,该加工中心故障间隔时间所服从的分布不会是正态分布或对数正态分布,而可能是指数分布或威布尔分布。
- 1. 2 MTBF的经验分布函数
式中:T―――故障间隔时间总体;t―――任意故障间隔时间。
设t1,t2,……,tn为故障间隔时间的观测值,由该组观测值所得到的故障间隔时间的顺序统计量为
t(1), t(2),……, t(n),则该加工中心故障间隔时间的经验分布函数为: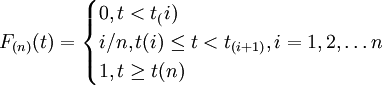 (3)
(3)
当样本容量n足够大时,用样本观测值所求出的经验分布函数F(n)(t)与理论分布函数F(t)之差的最大值便足够的小,此时可由F(n)(t)来估计F(t)。
故障间隔时间的分布函数F(t)同其密度函数f(t)之间的关系为: f(t)=F′(t) (4) 若故障间隔时间概率密度函数f(t)呈峰值形,如正态分布和对数正态分布,则分布函数F(t)将出现拐点。即: f′(t)=0→F″(t)=0 (5) 若故障间隔时间的概率密度函数f(t)呈单调下降趋势,则其分布函数F(t)在正半轴上将是凸的。即: f′(t)<0→F″(t)<0 (6)同理,若故障间隔时间概率密度函数f(t)呈单调上升趋势,则分布函数F(t)在正半轴上将是凹的。
由上述讨论可知,由经验分布函数F(n)(t)可估计理论分布函数F(t),而由F(t)的形状可初步判断f(t)的形状,所以由F(n)(t)的形状亦可初步判断f(t)的形状。
由式(3)可知,F(n)(t)的图形是阶梯形折线图,为拟合出F(n)(t)的连续曲线,将式(3)简化为:F(n)(t)=i/n,i=1,2,……,n (7)
下面对F(n)(t)进行拟合。将该系列加工中心故障间隔时间的观测值t∈[7.06,1494.51]分为13组。以每组时间的中值为横坐标,每组的累积频率为纵坐标,由此拟合出的F(n)(t)的曲线如图6所示。
由图可知,故障间隔时间的经验分布函数F(n)(t)为外凸,无拐点。可见,该加工中心故障间隔时间所服从的分布不会是正态分布或对数正态分布,而可能是指数分布或威布尔分布。
- 2 故障间隔时间分布模型的拟合检验
已知该加工中心故障间隔时间可能服从指数分布或威布尔分布。而威布尔分布包含指数分布。所以假设故障间隔时间服从威布尔分布,为确定该加工中心故障间隔时间分布规律,可用最小二乘法进行参数估计,并运用相关系数法来检验威布尔分布。
- 2. 1 初选分布模型
通常在实际应用时,我们假设产品刚刚投入生产时产品便发生故障。这样就可以用两参数威布尔分布对故障间隔时间的分布规律进行研究。
则公式为:![f(t)=\frac{\beta}{\alpha}(\frac{t}{\alpha})^{\beta-1}exp[-(\frac{t}{\alpha})^\beta],t\ge 0](http://wiki.mbalib.com/w/images/math/a/d/a/ada2c3e9097c7d800f56b936293692ca.png) (8)
(8)
![F(t)=1-exp[-(\frac{t}{\alpha})^\beta],t\ge 0](http://wiki.mbalib.com/w/images/math/5/9/4/5948e469c28b427314b42d53a9fa2120.png) (9)
(9)
- 2. 2 参数估计
- (1) 一元线性回归模型
分布类型的参数估计方法可分为图估计法、矩法、极大似然法及最小二乘法等。对于威布尔分布、极值分布等不含积分的累积分布函数采用一元线性回归方法进行参数估计。
假设试验中获得n对试验数据:(x1,y1)、(x2,y2)、……、(xn,yn),将它们标在直角坐标纸上,从图形上
看,数据点大体上散布在某条直线周围,变量间近似地呈现为线性关系。可作一直线,设直线方程为: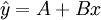
式中,参数B为该直线的斜率,A为截矩。
- (2)用最小二乘法进行参数估计
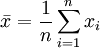
 (10) 则用最小二乘法估计出参数A、B的估计量为:
(10) 则用最小二乘法估计出参数A、B的估计量为:
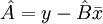
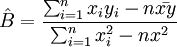 (11) 代入上述直线方程中,即得到y对x的一元线性回归方程:
(11) 代入上述直线方程中,即得到y对x的一元线性回归方程:
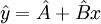 (12)
(12)
首先将试验所得到的故障间隔时间数据ti按由小到大的次序排列,并取中位秩作为各试验点的У值。然后假设一种分布类型,进行变换后,即可用式(1-14)式进行计算,估计得系数B、A后,即可进行原函数的参数估计。
对于两参数威布尔分布,其累积分布函数为: F(t) = 1 [exp (t / α)β] (13)式中:t≥0;k > 0,k为形状参数;b > 0,b为尺寸参数。
对式(1-15)两端进行变换,并取自然对数得:![\ln \ln \Big \{1/\bigg [(1-F(t))\bigg ]\Big \}=\beta\ln t-\beta \ln \alpha](http://wiki.mbalib.com/w/images/math/e/8/5/e8548d9e0c09031bdf5a5edc2d03c5d7.png) (14)
(14)
令:![y=\ln \ln \Big \{1/\bigg [(1-F(t))\bigg ]\Big \}](http://wiki.mbalib.com/w/images/math/c/4/5/c45dfa31699a4fcd6b30ff368ecc8408.png) ,x = lnt,B=β,A=-βlnα
,x = lnt,B=β,A=-βlnα
则:y=A+BX (15)
通过最小二乘法对威布尔分布的两参数进行估计。求得:B=0.864,A=-5.5714
又因为B=β,A=-βlnα,所以β=0.864,α=631.746
- 2. 3 威布尔分布的假设检验
- (1)线性相关性检验
![\hat{\rho }=\frac{\sum_{i=1}^n x_iy_i-n\bar{xy}}{\sqrt{[\sum_{i=1}^n x_i^2-nx^2][\sum_{i=1}^n y_i^2-ny^2]}}](http://wiki.mbalib.com/w/images/math/7/5/d/75db8bf6f5f329718d01a2ed4af72db8.png) (16)
(16)
相关系数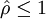 为线性相关,其值越接近1,表示x与y的线性相关性越强。当
为线性相关,其值越接近1,表示x与y的线性相关性越强。当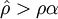 时,则也认为x与y是线性相关的。其中ρα是相关系数起码值,当n = 30,显著性水平= 0. 1时,相关系数起码值ρα = 0.3055。求得:
时,则也认为x与y是线性相关的。其中ρα是相关系数起码值,当n = 30,显著性水平= 0. 1时,相关系数起码值ρα = 0.3055。求得: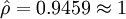 ,且
,且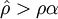 所以x与y是线性相关的,即线性回归的效果是显著的。
所以x与y是线性相关的,即线性回归的效果是显著的。
- (2)分布拟合的假设检验
常用的拟合优度检验方法有x2检验法和d检验法。x2检验法一般只用于大样本,而且对于截尾样本容易犯第Ⅱ类错误;d检验法比x2检验法精细,而且实用于小样本的情况。本加工中心的故障数据比较适用于d检验。所以将对该系列加工中心故障间隔时间的分布函数进行d检验。
d检验法的拒绝域为: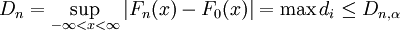 (17)
(17)
式中:F0(x)―――原假设分布函数;Fn(x)―――样本大小为n的经验分布函数;Dn,α―――临界值。
将n个试验数据按由小到大的次序排列,根据假设的分布,计算每个数据对应的F0(xi),将其与经验分布函数Fn(xi)进行比较,其中差值的最大绝对值即检验统计量Dn的观察值。将Dn与临界值Dn,α进行比较。满足下列条件,则接受原假设,否则拒绝原假设。
假设故障间隔时间服从威布尔分布F(t)=1-[exp-(t/631.746)0.864]
可求得:Dn,α=0.2227 Dn=0.158,因为Dn,α>Dn,故接受原假设。
所以故障间隔时间(MTBF)服从威布尔分布。
- 3 结论
该系列加工中心故障符合威布尔分布;分布模型为:F(t)=1-[exp-(t/631.746)0.864]。
由此可以进行故障预测,预测下一次故障发生的时间间隔,为保证数控机床可靠性提供理论基础。