海量数据解决思路之BitMap
一、概述
本文将讲述Bit-Map算法的相关原理,Bit-Map算法的一些利用场景,例如BitMap解决海量数据寻找重复、判断个别元素是否在海量数据当中等问题.最后说说BitMap的特点已经在各个场景的使用性。
二、Bit-Map算法
先看看这样的一个场景:给一台普通PC,2G内存,要求处理一个包含40亿个不重复并且没有排过序的无符号的int整数,给出一个整数,问如果快速地判断这个整数是否在文件40亿个数据当中?
问题思考:
40亿个int占(40亿*4)/1024/1024/1024 大概为14.9G左右,很明显内存只有2G,放不下,因此不可能将这40亿数据放到内存中计算。要快速的解决这个问题最好的方案就是将数据搁内存了,所以现在的问题就在如何在2G内存空间以内存储着40亿整数。一个int整数在java中是占4个字节的即要32bit位,如果能够用一个bit位来标识一个int整数那么存储空间将大大减少,算一下40亿个int需要的内存空间为40亿/8/1024/1024大概为476.83 mb,这样的话我们完全可以将这40亿个int数放到内存中进行处理。
具体思路:
1个int占4字节即4*8=32位,那么我们只需要申请一个int数组长度为 int tmp[1+N/32]即可存储完这些数据,其中N代表要进行查找的总数,tmp中的每个元素在内存在占32位可以对应表示十进制数0~31,所以可得到BitMap表:
tmp[0]:可表示0~31
tmp[1]:可表示32~63
tmp[2]可表示64~95
.......
那么接下来就看看十进制数如何转换为对应的bit位:
假设这40亿int数据为:6,3,8,32,36,......,那么具体的BitMap表示为:
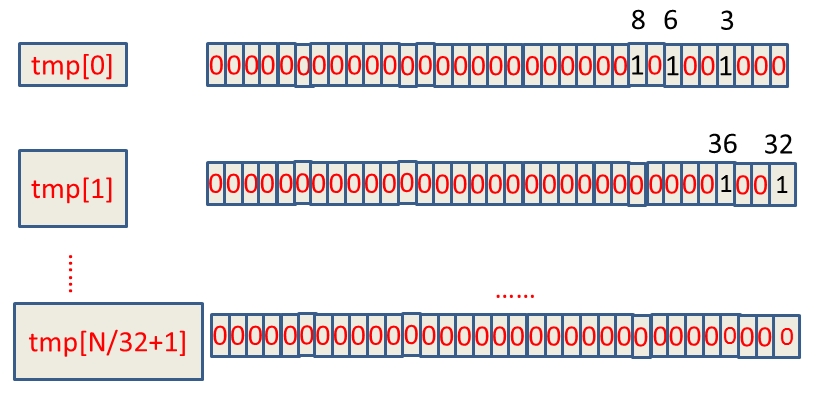
如何判断int数字在tmp数组的哪个下标,这个其实可以通过直接除以32取整数部分,例如:整数8除以32取整等于0,那么8就在tmp[0]上。另外,我们如何知道了8在tmp[0]中的32个位中的哪个位,这种情况直接mod上32就ok,又如整数8,在tmp[0]中的第8 mod上32等于8,那么整数8就在tmp[0]中的第八个bit位(从右边数起)。
三、Bit-Map算法原始实现
标注下,这部分来自blog:http://blog.csdn.net/hguisu/article/details/7880288的第五部分。好,来看看c语言的实现:
//set 设置所在的bit位为1
void set(int i) {
a[i>>SHIFT] |= (1<<(i & MASK));
}
//clr 初始化所有的bit位为0
void clr(int i) {
a[i>>SHIFT] &= ~(1<<(i & MASK));
}
//test 测试所在的bit为是否为1
int test(int i){
return a[i>>SHIFT] & (1<<(i & MASK));
}
int main()
{ int i;
for (i = 0; i < N; i++)
clr(i);
while (scanf("%d", &i) != EOF)
set(i);
for (i = 0; i < N; i++)
if (test(i))
printf("%d\n", i);
return 0;
}
注明: 左移n位就是乘以2的n次方,右移n位就是除以2的n次方
解析本例中的void set(int i) { a[i>>SHIFT] |= (1<<(i & MASK)); }
1) i>>SHIFT:
其中SHIFT=5,即i右移5为,2^5=32,相当于i/32,即求出十进制i对应在数组a中的下标。比如i=20,通过i>>SHIFT=20>>5=0 可求得i=20的下标为0;
2) i & MASK:
其中MASK=0X1F,十六进制转化为十进制为31,二进制为0001 1111,i&(0001 1111)相当于保留i的后5位。
比如i=23,二进制为:0001 0111,那么
0001 0111
& 0001 1111 = 0001 0111 十进制为:23
比如i=83,二进制为:0000 0000 0101 0011,那么
0000 0000 0101 0011
& 0000 0000 0001 0000 = 0000 0000 0001 0011 十进制为:19
i & MASK相当于i%32。
3) 1<<(i & MASK)
相当于把1左移 (i & MASK)位。
比如(i & MASK)=20,那么i<<20就相当于:
0000 0000 0000 0000 0000 0000 0000 0001 << 20
=0000 0000 0001 0000 0000 0000 0000 0000
注意上面 “|=”.
在博文:位运算符及其应用 提到过这样位运算应用:
将int型变量a的第k位清0,即a=a&~(1<<k)
将int型变量a的第k位置1, 即a=a|(1<<k)
这里的将 a[i/32] |= (1<<M));第M位置1 .
4) void set(int i) { a[i>>SHIFT] |= (1<<(i & MASK)); }等价于:
void set(int i)
{
a[i/32] |= (1<<(i%32));
}
即实现上面提到的三步:
1.求十进制0-N对应在数组a中的下标: n/32
2.求0-N对应0-31中的数:N%32=M
3.利用移位0-31使得对应32bit位为1: 1<<M,并置1;
四、BitMap算法一些其他应用场景扩展
(1)BitMap小小变种:2-BitMap。
看个小场景:在3亿个整数中找出不重复的整数,限制内存不足以容纳3亿个整数。
对于这种场景我可以采用2-BitMap来解决,即为每个整数分配2bit,用不同的0、1组合来标识特殊意思,如00表示此整数没有出现过,01表示出现一次,11表示出现过多次,就可以找出重复的整数了,其需要的内存空间是正常BitMap的2倍,为:3亿*2/8/1024/1024=71.5MB。
具体的过程如下:
扫描着3亿个整数,组BitMap,先查看BitMap中的对应位置,如果00则变成01,是01则变成11,是11则保持不变,当将3亿个整数扫描完之后也就是说整个BitMap已经组装完毕。最后查看BitMap将对应位为11的整数输出即可。
(2)对没有重复元素的整数进行排序。
对于非重复的整数排序BitMap有着天然的优势,它只需要将给出的无重复整数扫描完毕,组装成为BitMap之后,那么直接遍历一遍Bit区域就可以达到排序效果了。
举个例子:对整数4、3、1、7、6进行排序
BitMap如下:
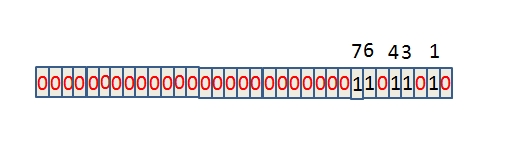
直接按Bit位输出就可以得到排序结果了。
五、总结
本文主要讲述了BitMap算法的相关概念以及其一些相关的应用场景和实现方法。其实BitMap的应用场景远远不止点,比如还可以用于压缩、爬虫系统中url去重、解决全组合问题。可能有些人觉得BitMap算法实现起来有点麻烦,其实某些语言是对BitMap算法进行了封装的,比如java中对应BitMap的数据结构就有BitSet类。其使用方法相当简单,看看API就ok,还是给个例子吧:
import java.util.BitSet;
public class Test{
public static void main(String[] args) {
int [] array = new int [] {1,2,3,22,0,3};
BitSet bitSet = new BitSet(6);
//将数组内容组bitmap
for(int i=0;i<array.length;i++)
{
bitSet.set(array[i], true);
}
System.out.println(bitSet.size());
System.out.println(bitSet.get(3));
}
}
对应的bit位如果有对应整数那么通过bitSet.get(x)会返回true,反之false。其中x为BitMap位置下标。
好了,BitMap就说到这里。下次blog说说处理海量数据的“万金油”-Hash算法,以及它在MapReduce框架中的应用。
参考文献:
http://blog.csdn.net/v_july_v/article/details/6685962
文章第三部分来自于:http://blog.csdn.net/hguisu/article/details/7880288