OpenSSL之安全通讯基础

安全特性：

任何一套安全的通讯系统在数据传输过程中至少具备以下三个特性：

              1，验证来源的合法性
              2，保证数据的完整性
              3，保证数据的私密性

对称加密：

对数据的私密性要求，我们可以通过对数据进行加解密来完成。如下图所示：

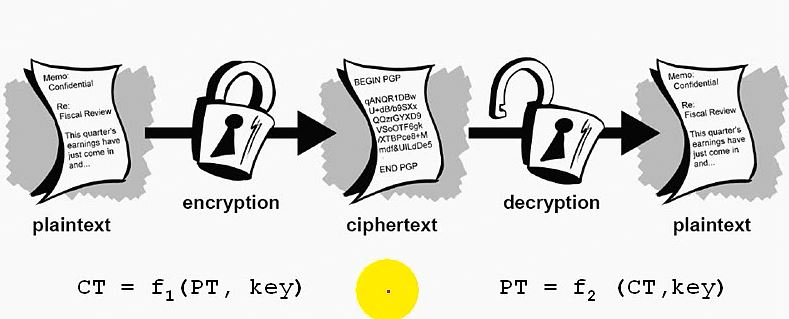
数据加密(encryption):使用一个密钥(key)并通过一种加密算法将明文(plaintext)

                     加密成密文(ciphertext)。

数据解密(decryption):是数据加密的逆向过程。通过密钥将密文解密成明文。

注：图中加解密的Key可以是同一个密钥，也可以是不同的密钥。

根据加解密Key的不同将加密体系分为两种：

                1，对称加密
                       特点：使用同一个密钥进行加解密
                       优点: 加密速度快
                       缺点：秘钥传递问题
                       常见的对称加密算法有：DES，3DES，AES等
                2，非对称加密
                       特点：数据传输双方事先都必须产生一对密钥
                             一个称为公钥
                             一个称为私钥
                             公钥加密的数据，只有对应的私钥才能解密
                             私钥加密的数据，只有对应的公钥才能解密
                       优点：解决了秘钥传递问题 
                       缺点：加密速度慢  
                       常见的非对称加密算法有：RSA，DH等

对称加密图例：

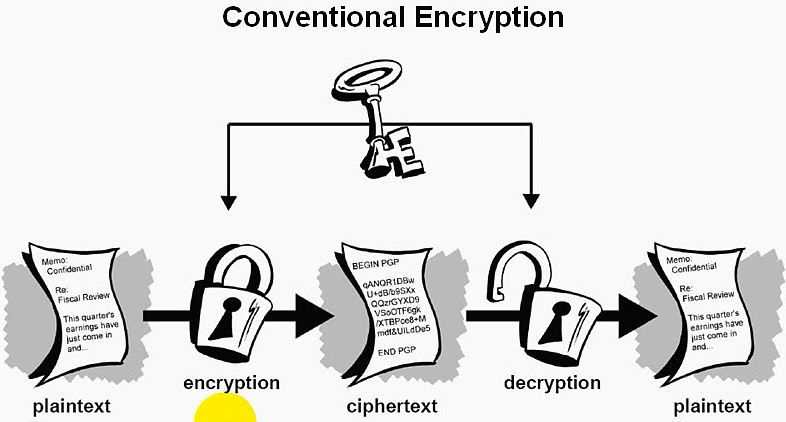
              图注: 发送方利用自己的密钥(Key)对明文数据进行加密；

                    接收方必须得到发送方的密钥(Key)；

                    接收方利用发送方的密钥对密文进行解密；

                    如果密钥在传输过程中被第三方获悉，那此次加密的私密性得不得保障。

                    

对称加密openssl实现：

加密数据：
格式：openssl enc  -ciphername -k password -in file1 -out file2
说明：
      enc              加密关键字
      -ciphername      指定加密算法
      -k               指定口令关键字
      password         口令
      -in              指定输入文件(file1)
      -out             指定输出文件(file2)  
      
 解密数据：
 格式：openssl enc -ciphername -k password -d -in file -out file2
 说明：-d              解密
       其他参数同上
 
 openssl支持的加密算法：DES,DES3,RC2,RC5,AES256等 
     
 实例：
       加密：
       openssl enc -des3 -k 123456 -in test.txt -out test.bin
       
       解密：
       openssl enc -des3 -k 123456 -d -in test.bin -out test1.txt

非对称加密：

非对称加密图例：

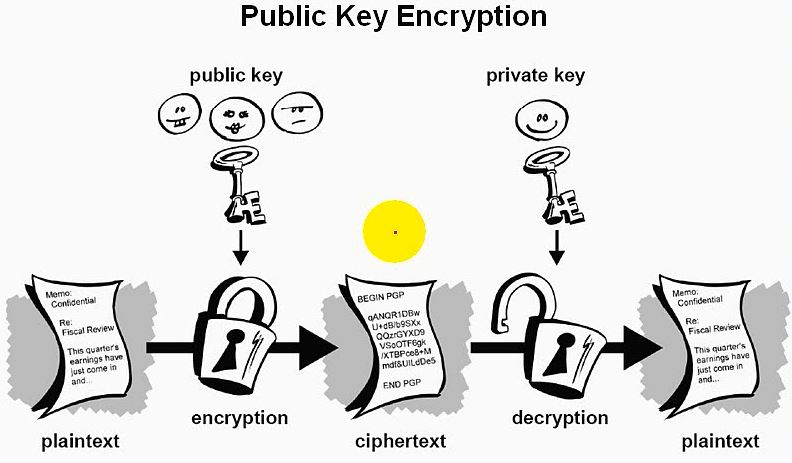
               图注：首先通讯双方都产生一对密钥；

                     数据发送方得到数据接收方的公钥；

                     数据发送方利用数据接收方的公钥对数据进行加密；

                     数据接收方利用自己的私钥对加密数据进行解密；

                     数据接收方最终得到明文的数据。

                     任何一方得到接收方的公钥，也解密不了传输中的数据。

非对称加密openssl实现：

产生密钥对：
格式：openssl genrsa -out file 1024
      openssl rsa -in file -pubout
说明：
      genrsa         使用rsa算法产生密钥
      -out           指定输出文件
      1024           指定算法强度 单位bit
      rsa            使用rsa算法产生密钥
      -in            指定输入文件
      -pubout        从私钥中提取公钥
      
使用公钥加密数据:
格式： openssl rsautl -in file -out file -inkey file -pubin -encrypt
说明：
       rsautl        使用rsautl对文件进行加密
       -in           指定输入文件(需要被加密的文件)
       -inkey        指定输入密钥文件
       -pubin        指定-inkey输入的是一个公钥文件
       -encrpt       表示加密
       
使用私钥解密：
格式： openssl rsautl -in file -out file -inkey file -decrypt
说明：
       -inkey        指定输入密钥文件(这里应该是私钥文件)
       -decrypt      表示解密
       其他同上
       
实例：
      产生密钥对：
      openssl genrsa -out priv.key 1024             //产生私钥
      openssl rsa -in priv.key -pubout > pub.key    //提取公钥
      
      使用公钥加密数据：
      openssl rsautl -in test.txt -out test.bin -inkey pub.key -pubin -encrypt
      
      使用私有解密：
      openssl rsautl -in test.bin -out test2.txt -inkey priv.key -decrypt

总结：虽然非对称加密体系实现了密钥交换的问题，但其本身算法实现复杂导致其加密速度慢。

于是在使用中，人们一般将对称加密和非对称加密二者结合起来使用。

对称与非对称结合：

混合使用之加密图解：

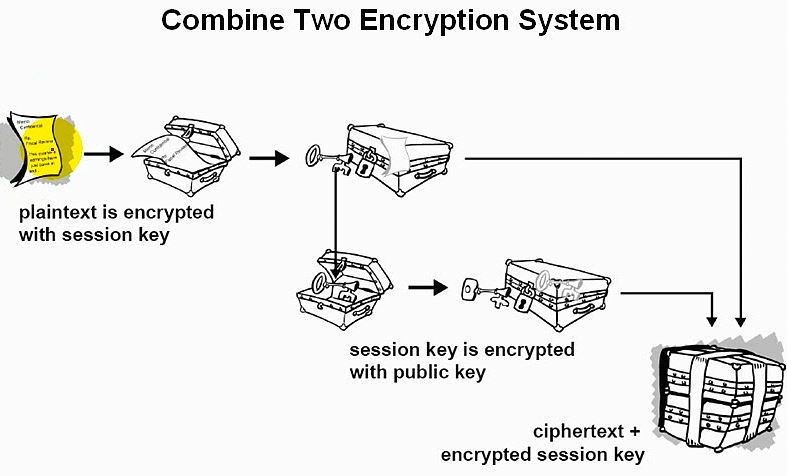
               图注：首先发送方利用一个随机数产生了一个对称密钥(session key);

                     发送方利用这个session key对数据进行加密；

                     发送方拿着接收方的公钥对这个session key进行加密；

                     发送方将加密好的数据和加密好的session key发送给接收方；

                     这种方法既保证了加密速度，又保证了加密密钥的安全传送。

混合使用之解密图解：

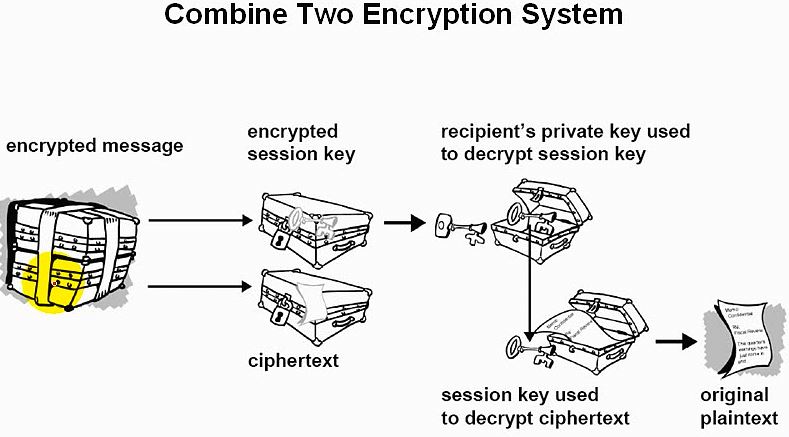
               图注：接收方接收到加密的数据和加密的session key；

                     接收方利用自己的私钥解密加密的session key；

                     接收方再利用已解密的session key来解密加密的数据文件；

                     接收方最终得到了明文的数据。

总结：虽然混合使用对称加密和非对称加密之后，既保证了加密速度，又保证了加密密钥的安全传送。

但是始终没办法保证来源的合法性。这时候就需要用到数字签名(Digital Signature)。

数字签名：

数字签名图解：

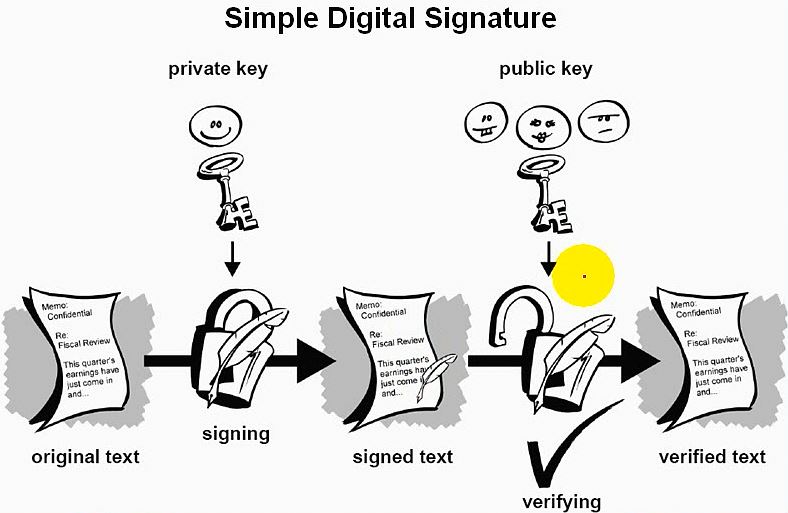
               图注：发送方使用自己的私钥加密数据文件(数字签名)；

                     接收方接收到这个数字签名文件；

                     接收方使用发送方的公钥来解密这个数字签名文件；

                     如果能够解开，则表明这个文件是发送方发送过来的；

                     否则为伪造的第三方发送过来的。

                     对于发送方来讲这种签名有不可否认性。

数字签名openssl实现：

产生密钥对：
格式：openssl genrsa -out file 1024
      openssl rsa -in file -pubout
      
使用私钥完成签名：
格式：openssl rsautl -in file -out file -inkey file -sign
说明：
      -inkey 后面跟私钥
      -sign  表示签名
      
使用公钥校验签名：
格式：openssl rsautl -in file -out file -inkey file -pubin -verify
      -inkey  后面跟公钥
      -verify 表示校验签名
      
实例：
      签名：
      openssl rsautl -in test.txt -out test.sig -inkey priv.key -sign
      
      校验签名：
      openssl rsautl -in test.sig -out test3.txt -inkey pub.key -pubin -verify

总结：非对称加密中，公钥加密，私钥解密。主要用来进行数据加密。

                    私钥加密，公钥解密。主要用来进行数字签名和认证。

到目前为止，解决了数据传输过程中数据私密性和来源合法性的问题。但是数据的完整性有靠什么来保障呢？这就要利用散列函数来实现。

散列函数：

散列函数的特点：

              1，输入可以是任意长度 但输出是定长的。MD5 128bits  SHA1 160bits

              2，加密过程不可逆，无法根据特征码还原原来的数据

              3，雪崩效应  输入的一点点改变 会导致结果发生很大改变

              4，输入一致，输出必然相同

             注：不同的输入，可能会有同样的输出。但是概率很小 并不代表没有这种可能

常见的散列函数(Hash函数)：

              1，MD5

              2，SHA1

散列函数openssl实现：

产生一个文件的MD5值：
格式： openssl dgst -md5 file
       md5sum file
       
产生一个文件的SHA1值：
       openssl dgst -sha1 file
       sha1sum file
       
实例：
       openssl dgst -md5 openssl-0.9.8h.tar.gz
       md5sum  openssl-0.9.8h.tar.gz
       
       openssl dgst -sha1 openssl-0.9.8h.tar.gz
       sha1sum openssl-0.9.8h.tar.gz

总结：散列函数可以根据任意长度的输入，生成定长的摘要信息。这样可以用来校验文件的完整性。

防止数据在传输过程中被第三方篡改。

安全数字签名：

安全数字签名图解：

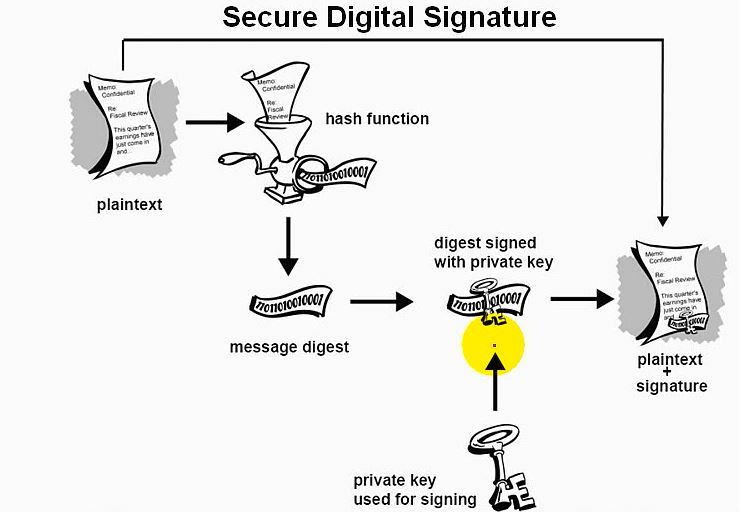
               图注：发送方利用散列函数对明文数据进行Hash得到摘要信息；

                     发送方使用自己的私钥对摘要信息进行签名；

                     接收方利用发送方的公钥来验证来源的合法性；

                     接收方利用摘要信息来验证数据的完整性；

                  注：

                     当源文件很大，如果对源文件进行签名，就会比较耗费时间。

                     如果只对摘要信息进行签名，速度比较快，因为它是定长的且位数不长。

中间人攻击：

利用散列函数我们可以用来保证数据的完整性。使用对称加密和非对称加密体系来完成数据的机密性和验证来源的合法性。但验证来源的合法性其实存在一个缺陷，就是怎么保证公钥的合法性？我们来看下图中的例子：

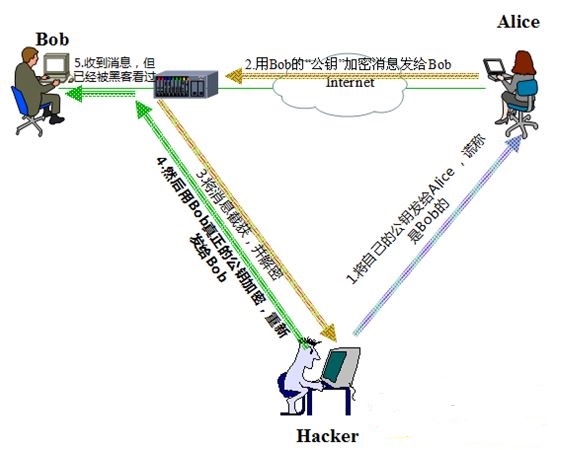
               图注：假设Alice想向Bob发送一个文件。

                     首先Alice得得到Bob的公钥；

                     但是很不幸，Alice得到的是Hacker使用自己的公钥伪装成Bob的公钥；

                     于是Alice拿着这个伪装的公钥对文件进行加密，并发送给Bob；

                     但不幸的事情又发生了，这个加密文件被Hacker截获；

                     于是，Hacker得到了文件的内容；

                     Hacker对原文件可能进行篡改/也可能不会篡改；

                     这样看Hacker的目的；

                     于是Hacker利用Bob真正的公钥对文件进行加密；

                     然后发送给Bob；

                     整个过程对Bob和Alice来说全然无知。

通过上图，我们看出要想实现对公钥来源合法性进行验证。就必须得引入另一个角色。首先数据通讯双方都得信任这个角色。也就是这个角色具有权威性。其次，这个角色可以帮助通讯双方安全完成公钥交换。我们通常把这样一个角色或机构称为CA。

引入CA：

利用CA完成整个安全通讯过程：

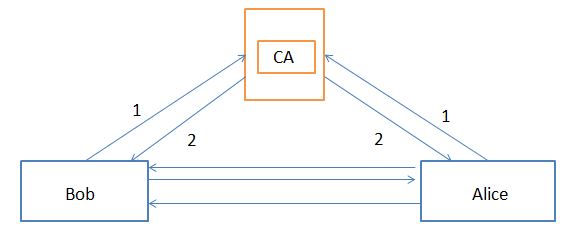
               图注：

                    1，首先必须保证CA为数据通讯双方都认可的机构；

                    2，数据通讯双方向CA提交认证申请。里面包含各自的公钥；

                    3，CA分别对通讯双方的合法性进行验证；

                       如果验证通过，CA则利用自己的私钥分别对两份申请文件

                       进行加密(数字签名)。最终产生一个由CA完成数字签名的文件。

                       我们把这个文件称为数字证书。

                    4，通讯双方各自下载由CA签发的数字证书；

                    5，假设Alice想要发送一个文件给Bob；

                    6，首先Alice得向Bob请求得到Bob的数字证书；

                    7，Alice利用CA的公钥完成对Bob数字证书合法性认证，

                       并且从证书中得到Bob的公钥。

                    8，Alice利用散列函数对数据进行Hash产生摘要信息；

                       并通过程序随机生成一个session key,

                       利用这个session key对数据进行加密；

                       Alice再利用Bob的公钥对这个session key进行加密；

                    9，Alice将自己的证书和加密后的文件(包含session key)一并发送给Bob；

                    10,Bob接收到Alice发来的文件后，先用CA的公钥来验证文件来源的合法性。

                       如果合法，则利用自己的私钥对session key进行解密，

                       再利用session key对数据进行解密，得到明文数据。

                       然后，利用散列函数对数据进行Hash得到摘要信息。

                       将自己得到的摘要信息和Alice发过来的摘要信息进行比对，

                       如果一致，则表明数据没有被篡改。安全通讯完成。