ssh秘钥交换详解与实现 diffie-hellman-group-exchange-sha
ssh的DH秘钥交换是一套复合几种算法的秘钥交换算法。在RFC4419中称为diffie-hellman-groupX-exchange-shaX 的算法(也有另一种单纯的 rsaX-shaX 交换算法)。本文就以diffie-hellman-group-exchange-sha256为例,详尽地讲解整个完整的秘钥交换过程。
笔者在RFC上和网上看了很久,也只是做了一个大致了解,对实现的帮助不大。实际在实现过程中,有太多的细节需要注意,在很多细节的分歧中,需要自己抱着勇气去测试。(原谅我不看openssh源码和使用openssl库,我只想全部自己实现整个ssh)。在diffie-hellman-group-exchange-sha256中,数据的类型非常地重要,因为涉及到hash运算,一定要区别好整数与字符串还有进制。一个小的不同都会导致hash的结果大不一样,hash错了以后的工作都是徒劳。
diffie-hellman-group-exchange-sha256的整个过程中一共要用到的秘钥交换算法有:diffie-hellman、sha256、ssh-rsa(或其他算法协商的host key,不是单纯的rsa,虾米告诉我ssh用的是RSASSA-PKCS1-v1_5 scheme标准)。而要支持这些加密算法,又需要很多基础算法:多进制大整数、高精度运算、快速模幂、离散算法...(还好自己有一定的acm基础,本来当初是打算学习并实现ssh协议,结果在算法的道路上越走越远,这次就当锻炼自己了。表示以后要好好运用面向对象技术,再也不实现不必要的底层了,以后涉及到安全传输就直接用openssl了)
以下为各个算法的讲解,先说最重要的几个基础数据结构与计算方法:
1、mpint: 二进制补码格式的多精度整数,储存为一个字符,每个字符8位,从高位到低位,负数最高位为1,正数最高位为0(只用到整数)。数据格式为:4字符长度+该长度字符的数值。例如:a1d8:00 00 00 03 00 a1 d8; 4:00 00 00 02 00 04
2、多进制大整数:平时以16进制存储,这样便于使用的时候少转化,转二进制也很快,实现很麻烦,我虽然有自己的大整数模板,但终归是不放心,我就用cryptopp自带的大整数改写过来用(人家可是用的汇编计算的)。
3、高精度运算:主要实现加法乘法和求余即可,因为dh和rsa只需要用到乘法与求余。
4、快速模幂:DH算法和RSA算法都会用到相似的运算:a^b%c 。因为b是一个大整数,因此对于他的幂运算我们将b进行二分,然后对a以及a计算后的结果进行计算,这样能省下大量不必要的运算。几个例子:3^8=3*3*3*3*3*3*3*3要进行7次运算。而这样化解(3^4)*(3^4)=(3^4)^2=((3^2)*(3^2))^2=((3^2)^2)^2只需要进行3次运算。第一种方式的时间复杂度是O(n),第二种二分幂的方法时间复杂度是O(logn),当b为10位十进制的整数时,第一种方式要计算10^10次,而用二分幂的方式只需要计算大约30多次。因为我们要求的是余果,所以在进行幂运算的同时就进行模运算,也能极大减少运算量,否则内存可能都装不下那么大的幂果。下面给出代码实现:
Integer fastpower_comp(Integer a,Integer b,Integer c)
{
/*sample unused fast power
Integer re=1;
for(int i=0;i<b;i++)
{
re*=a;
re%=c;
}
return re;
*/
//fast power
Integer n=c;
c=1;
while(b!=0)
{
if(b%2!=0)
{
b=b-1;
c=(c*a)%n;
}
else
{
b=b/2;
a=(a*a)%n;
}
}
return c;
}
密码算法:
1、diffie-hellman:
服务器首先产成两个数G、P,P为一个非常大的素数,作为DH算法的模;G为密码发生器,也就是P的一个原根(不理解没关系),服务器将这两个数发给客户端,用于秘钥的交换。
客户端生成一个数(客户端的私钥)x(0<x<P,但x应该大一点,否则当G特别小时生成的秘钥长度可能会很短,服务器会拒绝),计算e=(G^x)%P。得到的e就是客户端的公钥,客户端将e发送给服务器。
服务器也同客户端一样,生成一个数y,计算f=(G^y)%P。将服务器公钥f发送给客户端。
现在客户端与服务器都知道了对方的公钥,双方把对方的公钥作为自己模幂运算的底数进行运算,服务器计算K1=(e^y)%P,客户端计算K2=(f^x)%P 可以证明这里K1==K2 ,得到的K值便是双方所交换的秘钥。
大素数的生成:我采用了一种猜测加枚举的的方法。做过筛法算素数的都知道当数越大,出现连续素数的概率越高,而且连续的长度越长。我们可以通过随机生成一个大数(最好是奇数),然后判断该素数是否为素数,如果不是,将这个数加二再判断,直到判断为素数即可,以后每次再要取素数就可以把这个结果加再判断(此时素数的几率很高)。
class m_dh
{
public:
Integer dh_g,dh_p,dh_x,dh_e;
Integer dh_y,dh_f;
Integer dh_k;
void set_g_and_p(const Integer g,const Integer p)
{
dh_g=g;
dh_p=p;
}
void set_y(Integer y)
{
dh_y=y;
}
void set_f(Integer f)
{
dh_f=f;
}
void comp_e();
Integer get_e()
{
return dh_e;
}
void comp_k();
Integer get_k()
{
return dh_k;
}
};
void m_dh::comp_e()
{
dh_x=mkrandomnum(50)+1;
dh_e=fastpower_comp(dh_g,dh_x,dh_p);
}
void m_dh::comp_k()
{
dh_k=fastpower_comp(dh_f,dh_x,dh_p);
}
2、rsa:
这里讲的是裸的rsa算法。
服务器生成两个不同的素数p和q,计算出模n=p*q,并计算欧拉函数φ(n) = (p-1)(q-1)。服务器再在1到φ(n) 之间生成一个与φ(n)互质的的数e找到另一个数d满足(e*d)%φ(n)==1。
现在服务器有三个数n、e、d ,ne的组合为rsa的公钥,nd为私钥。服务器将公钥发给客户端。在以后的加密解密中,公钥用于加密和签名验证,私钥用于解密与签名。
加密数字K:计算C=(K^e)%n,C即为加密后的数据 解密C得到K:K=(C^d)%n
签名采用相反的方式,即服务器用私钥加密,客户端用公钥解密,验证解密后的数据。
然而ssh-rsa使用的是 RSASSA-PKCS1-v1_5 scheme标准,他还含有一些其他的填充值,实际实现的时候需要考虑周全。
class m_rsa
{
public:
Integer rsa_e;
Integer rsa_n;
void set_e_and_n(Integer e,Integer n)
{
rsa_e=e;
rsa_n=n;
}
Integer comp_rsa_result(Integer num);
};
Integer m_rsa::comp_rsa_result(Integer num)
{
return fastpower_comp(num,rsa_e,rsa_n);
}
3、sha256
散列算法没什么可讲的,主要注意sha256的密文长度是64位的16进制,在进行rsa加解密以及计算sessionid的时候一定要注意关于长度的问题。使用的重点在于需要哪些值以什么样的一种组合方式去参与hash运算。
我就直接使用cryptopp的hash算法实现了:
class m_sha
{
public:
string encode_sha1(string data);
string encode_sha256(string data);
};
string m_sha::encode_sha256(string data)
{
string hash;
SHA256 sha256;
HashFilter hash_filter (sha256);
hash_filter.Attach(new HexEncoder(new StringSink(hash), false));
hash_filter.Put((byte *)data.c_str(),data.length());
hash_filter.MessageEnd();
return hash;
}
详细过程:
基本的算法了解了就可以来看diffie-hellman-group-exchange-sha256的整个过程了。

整个交换过程有5个数据包:按顺序分别是1、dh key exchange init;2、dh key exchange reply;3、dh gex init 4、dhgex reply 5、new keys
1、dh key exchange init(30)
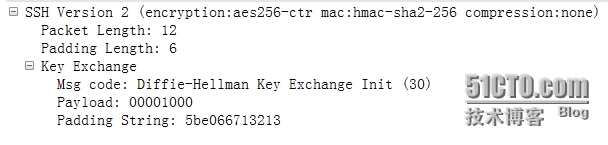
客户端告诉服务器开始DH交换。
2、dh key exchange reply(31)
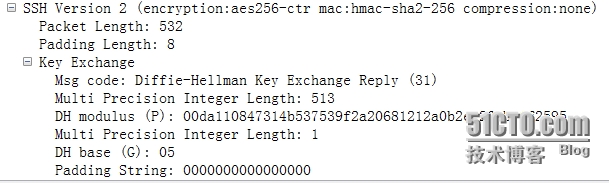
服务器将生成的P和G发给客户端。
3、dh gex init(32)
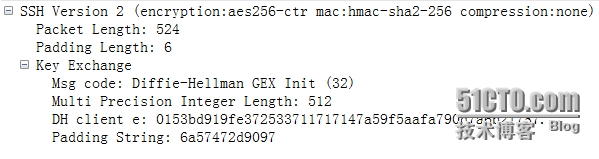
客户端收到服务器发过来的P和G后,自己计算出e返回给客户端
4、dh gex reply(33)

服务器收到客户端的e后,根据算法计算出秘钥值K。然后使用sha256算法将一些已知信息hash加密为H(具体过程后面会提到),并用rsa将hash值签名。最后发送rsa的公钥、dh的f值、rsa签名后的hash信息发回客户端。
5、new keys(21)

客户端根据服务器发回的f计算出同样的k值,并根据同样的已有信息hash计算得到H后使用服务器发来的rsa公钥校验服务器发回的hash值的签名,根据得到的hash值H即会话用的session_id,再进行特定的hash运算(参见下文)即可得到以后用于数据加密的秘钥。如果校验无误,返回new key(21),表示秘钥交换的过程完毕,以后的数据都将由所得秘钥进行加密。
H与session_id的计算:
H=hash(V_C||V_S||I_C||I_S||K_S||e||f||K);
按顺序用到的值(注意类型):
| 类型 | 值 | 说明 |
| string | V_C | 客户端的初始报文(版本信息:SSH-2.0-xxx,不含结尾的CR和LF) |
| string | V_S | 服务器的初始报文 |
| string | I_C | 客户端 SSH_MSG_KEX_INIT的有效载荷(不含开头的数据长度值) |
| string | I_S | 服务器的同上 |
| string | K_S | 主机秘钥(dh gex reply(33)过程服务器发送host key (RSA公钥)) |
| mpint |
e | 客户端DH公钥 |
| mpint | f | 服务器DH公钥 |
| mpint | K | 共同DH计算结果 |
将以上内容按顺序进行拼接,不要夹杂或尾随多余字符。将拼接后的字符串进行sha256计算出结果H。这个H就是session_id(会话第一次的秘钥交换生成的的H才是session_id,以后如果还要进行秘钥交换,session_id不会改变)。
加密秘钥计算:
这里的加密秘钥指的是以后数据通信所用的秘钥,一般用aes算法。
计算方式:hash(K,H,单个字符,session_id);
单个字符指的是单个大写的ASCII字母,根据不同的加密秘钥选择不同的字符来计算。
| 字母 | 秘钥 |
| 'A' | 客户端到服务器的初始IV(CBC) |
| 'B' | 服务器到客户端的初始IV |
| 'C' | 客户端到服务器的加密秘钥(数据加解密秘钥) |
| 'D' | 服务器到客户端的加密秘钥 |
| 'E' | 客户端到服务器的完整性秘钥(HMAC) |
| 'F' | 服务器到客户端的完整性秘钥 |
哈希计算得到字符串RE,如果我么想要的秘钥长度比RE长,则在RE后面继续加上一个hash值:hash(K,H,RE)成为一个加长的RE。还不够继续加上hash(K,H,RE),依次类推
ssh秘钥交换的过程就告一段落了。笔者在网上找不到合适资料,尤其是这些关于diffie-hellman-group-exchange-sha 的很多细节,自己苦逼了很长时间(本来打算两下撸完去学其他的)终于完成了了。希望给想要自己实现该算法的朋友给予帮助。如还遇到其他的问题可Q我(WCHRT)。