这一次,我将较为深入地探讨高斯滤波,包括参数的影响、参数的选取、高斯模板的形成以及自行编程实现高斯滤波的效果与openCV函数实现效果比对。
首先,我们接(一)中最后所述的内容继续开始探讨。在(一)中,我们最后探讨了一下关于高斯函数中的sigma的选取对于模板生成的影响和对滤波效果的影响,但是我在(一)中我未给详细地解释,这里我想比较通俗地并且具体地阐述一下这些影响的成因:
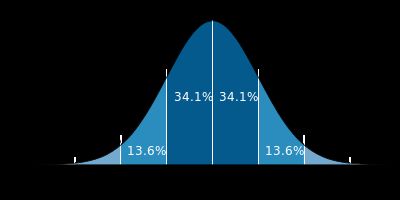
上回书说道“sigma表示的是标准差,如果标准差比较小,这是就相当于图像点运算,则平滑效果不明显;反之,标准差比较大,则相当于平均模板,比较模糊”,那么这么说可能很多人包括一开始的我并不是很理解,这是为什么呢,那么我们需要从高斯函数谈起:
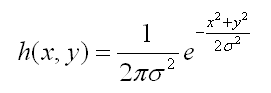
我们要理解好这个图,横轴表示可能得取值x,竖轴表示概率分布密度F(x),那么不难理解这样一个曲线与x轴围成的图形面积为1。sigma(标准差)决定了这个图形的宽度,我给出下述结论:sigma越大,则图形越宽,尖峰越小,图形较为平缓;sigma越小,则图形越窄,越集中,中间部分也就越尖,图形变化比较剧烈。这其实很好理解,如果sigma也就是标准差越大,则表示该密度分布一定比较分散,由于面积为1,于是尖峰部分减小,宽度越宽(分布越分散);同理,当sigma越小时,说明密度分布较为集中,于是尖峰越尖,宽度越窄!
理解好上述结论之后,那么(一)中的结论当然也就顺理成章了,sigma越大,分布越分散,各部分比重差别不大,于是生成的模板各元素值差别不大,类似于平均模板;sigma越小,分布越集中,中间部分所占比重远远高于其他部分,反映到高斯模板上就是中心元素值远远大于其他元素值,于是自然而然就相当于中间值得点运算。
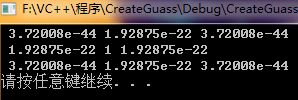
窗口尺寸:3*3 sigma = 0.8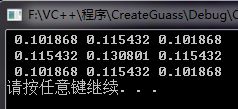
窗口尺寸:3*3 sigma = 2
接着,我们来重点讨论下高斯模板,在初学高斯滤波的时候,用得最多的也是最经典的一个3*3模板就是 1 2 1
[ 2 4 2 ]
1 2 1
,当时我就很纳闷这个模板是怎么出来的,后来我经过多方查找资料,基本得到了如下的解释:高斯模板实际上也就是模拟高斯函数的特征,具有对称性并且数值由中心向四周不断减小,这个模板刚好符合这样的特性,并且非常简单,容易被大家接受,于是就比较经典!但是这样一个简单的矩阵是远远不能满足我们对图像处理的要求的,我们需要按照自己的要求得到更加精确的模板,那么接下来我们就编程实现自己想要的高斯模板。部分关键函数如下:
double** createG(int iSize, double sigma)
{
double **guass;
double sum = 0;
double x2 = 0;
double y2 = 0;
int center = (iSize - 1) / 2;
guass = new double*[iSize];//注意,double*[k]表示一个有10个元素的指针数组
for (int i = 0; i < iSize; ++i)
{
guass[i] = new double[iSize];
}
for (int i = 0; i<iSize; i++)
{//使用x2,y2降低了运算速度,提高了程序的效率
x2 = pow(double(i - center), 2);
for (int j = 0; j<iSize; j++)
{
y2 = pow(double(j - center), 2);
sum += guass[i][j] = exp(-(x2 + y2) / (2 * sigma*sigma));
}
}
if (sum != 0)
{
//归一化
for (int i = 0; i<iSize; i++)
{
for (int j = 0; j<iSize; j++)
{
guass[i][j] /= sum;
}
}
}
return guass;
}
上述的这个函数就是返回的一个用户想要的高斯模板,其输入参数iSize表示模板大小(这里先只考虑方阵模板),输入参数sigma表示高斯函数标准差,聪明的你应该一眼就看出这个程序实际上就是按照公式根据规定的矩阵大小进行离散化得到相应的数据。纵观整个程序,我觉得最不好理解的是那个参数center,这是个什么参数呢?通过程序可以看出为什么center与iSize呈2center+1的关系呢?而且,为什么x2,y2是那样取值呢?这实际上是模拟的一种距离关系。举个例子来说:
假设我现在想要使用窗口尺寸为2k+1*2k+1的高斯模板对点进行操作,那么假设这个高斯模板的第一个元素地址记为为(1,1),那么高斯模板中心元素很容易算出为(k,k)。假设现在在计算模板中(i,j)元素值,那么公式中的x2模拟为该点到中心点的距离,即i-k-1(为什么要-1,读者不妨自己自己写个3*3的矩阵,看看(1,1)元素到(2,2)元素是不是要走两步)。但是程序中是没有-1的,这是因为程序中的i是从0开始的!于是这个center参数实际上就是代表的中心点!
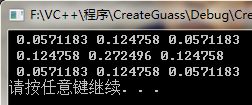
我的程序运行的结果:3*3,sigma=1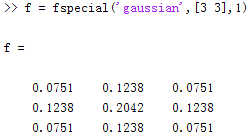
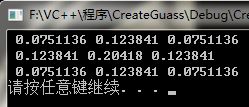
Matlab的程序运行的结果:3*3,sigma=1
可以看出,相差无几,这个程序是成功的!
然后,最重要的部分当然是使用上述高斯模板对图像进行滤波处理得到想要的效果,那么接下来重点论述滤波处理。要理解好高斯滤波,自己写高斯滤波的算法当然是最好的,然后再和openCV的函数进行效果比对,这样,算是对高斯滤波有了比较好的认识和理解了!
在很多资料上,我们都看到高斯函数的这样一个特性,可分离性,意思是一个二维的高斯函数可以分解成相同的一维高斯函数处理两遍,得到的效果是一样的,但是处理时间却大大缩短了。
我们可以想到,二维函数直接处理会是这样的:
for(int i = 0; i < img->height; ++i)
for(int j = 0; j < img->weigth; ++j)
{
for(int m = 0; m < iSize; ++m)
for(int n= 0; n< iSize; ++n)
{
...
}
}
这样的算法复杂度可以看出是为O(height*weigth*iSize^2)
然而使用分解后的一维函数进行两次处理,程序应当如下:
for(int i = 0; i < img->height; ++i)
for(int j = 0; j < img->weigth; ++j)
{
for(int m = 0; m < iSize; ++m)
{
...
}
}
for(int j = 0; j< img->weigth; ++j)
for(int i= 0; i< img->height; ++i)
{
for(int m = 0; m < iSize; ++m)
{
...
}
}
这样的算法复杂度为O(2*height*weigth*iSize),比一维处理要少了很多,所以时间对应来说也会快一点。
用后者,我们的关键函数如下:
/*
生成一维高斯模板,水平的和垂直方向上的模板是一样的
输入参数分别是:模板大小,sigma值
输出:一维数组(高斯模板)
*/
double* CreateMuban(int iSize ,double sigma)
{
double *gauss = new double[iSize];//声明一维模板
int radius = (iSize - 1) / 2;//这是高斯半径
double MySigma = 2 * sigma * sigma;
double value = 0;
for (int i = 0; i < iSize; i++)
{//高斯函数前面的常数项因为在归一化的时候将会消去,故这里不重复计算
gauss[i] = exp(-(i - radius)*(i - radius)/MySigma);
value = value + gauss[i];
}
for (int i = 0; i < iSize; i++)
{//归一化
gauss[i] = gauss[i] / value;
}
return gauss;
}
//对像素进行操作
IplImage* operatorImage(IplImage* img, double* Muban, int iSize)
{
//创建一张新的图片来进行滤波操作
IplImage* NewImage = cvCreateImage(cvSize(img->width, img->height), 8, 3);
int radius = (iSize - 1) / 2;
int r = 0;
int g = 0;
int b = 0;
CvScalar cs;
//复制图片
cvCopy(img, NewImage);
//先对I,也就是垂直方向进行操作
for (int j = 0; j < NewImage->width; ++j)
{
for (int i = 0; i < NewImage->height; ++i)
{
//先判断是否是边缘,不是则操作,是则跳过不处理,保持原样
if (!JudgeEdge(i, NewImage->height, radius))
{
for (int k = 0; k < iSize; ++k)
{
/* b = b + (int)((double)(NewImage->imageData + (i - radius + k) * NewImage->widthStep)[j * (int)NewImage->nChannels + 0] * Muban[k]);
g = g + (int)((double)(NewImage->imageData + (i - radius + k) * NewImage->widthStep)[j * (int)NewImage->nChannels + 1] * Muban[k]);
r = r + (int)((double)(NewImage->imageData + (i - radius + k) * NewImage->widthStep)[j * (int)NewImage->nChannels + 2] * Muban[k]); */
cs = cvGet2D(NewImage, i - radius + k, j); //获取像素
b = b + (int)((double)cs.val[0] * Muban[k]);
g = g + (int)((double)cs.val[1] * Muban[k]);
r = r + (int)((double)cs.val[2] * Muban[k]);
}
/*((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 0] = b; //改变该像素B的颜色分量
((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 1] = g; //改变该像素G的颜色分量
((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 2] = r; //改变该像素R的颜色分量 */
cs = cvGet2D(NewImage, i, j);
cs.val[0] = b;
cs.val[1] = g;
cs.val[2] = r;
cvSet2D(NewImage, i, j, cs);
b = 0;
g = 0;
r = 0;
}
}
}
//在对J,也就是水平方向进行操作
for (int i = 0; i < NewImage->height; ++i)
{
for (int j = 0; j < NewImage->width; ++j)
{
//先判断是否是边缘,不是则操作,是则跳过不处理,保持原样
if (!JudgeEdge(j, NewImage->width, radius))
{
for (int k = 0; k < iSize; ++k)
{
/*b = b + (int)((double)(NewImage->imageData + i * NewImage->widthStep)[(j - radius + k) * (int)NewImage->nChannels + 0] * Muban[k]);
g = g + (int)((double)(NewImage->imageData + i * NewImage->widthStep)[(j - radius + k) * (int)NewImage->nChannels + 1] * Muban[k]);
r = r + (int)((double)(NewImage->imageData + i * NewImage->widthStep)[(j - radius + k) * (int)NewImage->nChannels + 2] * Muban[k]);*/
cs = cvGet2D(NewImage, i, j - radius + k); //获取像素
b = b + (int)((double)cs.val[0] * Muban[k]);
g = g + (int)((double)cs.val[1] * Muban[k]);
r = r + (int)((double)cs.val[2] * Muban[k]);
}
/*((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 0] = b; //改变该像素B的颜色分量
((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 1] = g; //改变该像素G的颜色分量
((uchar *)(NewImage->imageData + i * NewImage->widthStep))[j * NewImage->nChannels + 2] = r; //改变该像素R的颜色分量*/
cs = cvGet2D(NewImage, i, j);
cs.val[0] = b;
cs.val[1] = g;
cs.val[2] = r;
cvSet2D(NewImage, i, j, cs);
b = 0;
g = 0;
r = 0;
//cout << r << " " << g << " " << b << endl;
}
}
}
return NewImage;
}
自己编的程序与openCV函数处理效果并无差别,成功!
最后,对高斯滤波部分进行扩展------自适应高斯滤波。为了达到更好的滤波效果,我们的手法需要更加灵活,往往可以加上一些限制条件进行判断是否需要处理。这一点很想PID控制中的选择积分的方法(具体名字忘了···囧)。这个我将在后面进行适当地尝试!
学习高斯滤波只是一个开始,但是学习其他的图像处理方法诸如此类,我要学会举一反三,而且要实践与理论紧密结合,真正做到知其甚解才好啊!