Leetcode: Range Sum Query 2D - Mutable && Summary: Binary Indexed Tree

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Range Sum Query 2D
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:
Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
update(3, 2, 2)
sumRegion(2, 1, 4, 3) -> 10
Note:
The matrix is only modifiable by the update function.
You may assume the number of calls to update and sumRegion function is distributed evenly.
You may assume that row1 ≤ row2 and col1 ≤ col2.

参考：https://leetcode.com/discuss/72685/share-my-java-2-d-binary-indexed-tree-solution

Build binary indexed tree takes :　　　O(mn*logm*logn) 　　time, both update() and getSum() take:    　　O(logm*logn) 　　time. The arr[][] is used to keep a backup of the matrix[][] so that we know the difference of the updated element and use that to update the binary indexed tree. The idea of calculating sumRegion() is the same as in Range Sum Query 2D - Immutable.

 

 

Summary of Binary Indexed Tree:

Binary Index Tree参见：https://www.youtube.com/watch?v=CWDQJGaN1gY

Compare Segment Tree vs Binary Indexed Tree

Segment Tree:

　　　　　　Time: O(N)build, O(logN)search, O(logN) update, 　　space: O(NlogN)

Binary Indexed Tree:

　　　　　　Time: O(NlogN)build, O(logN) search, O(logN) update, 　　space: O(N)

The advantage of Binary Indexed Tree over Segment Tree are:

require less space and very easy to implement

 

 1 public class NumMatrix {
 2   int m, n;
 3   int[][] arr;    // stores matrix[][]
 4   int[][] BITree; // 2-D binary indexed tree
 5 
 6   public NumMatrix(int[][] matrix) {
 7     if (matrix.length == 0 || matrix[0].length == 0) {
 8         return;
 9     }
10 
11     m = matrix.length;
12     n = matrix[0].length;
13 
14     arr = new int[m][n];
15     BITree = new int[m + 1][n + 1];
16 
17     for (int i = 0; i < m; i++) {
18       for (int j = 0; j < n; j++) {
19         update(i, j, matrix[i][j]); // init BITree[][]
20         arr[i][j] = matrix[i][j];   // init arr[][]
21       }
22     }
23   }
24 
25   public void update(int i, int j, int val) {
26     int diff = val - arr[i][j];  // get the diff
27     arr[i][j] = val;             // update arr[][]
28 
29     i++; j++;
30     while (i <= m) {
31       int k = j;
32       while (k <= n) {
33         BITree[i][k] += diff; // update BITree[][]
34         k += k & (-k); // update column index to that of parent
35       }
36       i += i & (-i);   // update row index to that of parent
37     }
38   }
39 
40   int getSum(int i, int j) {
41     int sum = 0;
42 
43     i++; j++;
44     while (i > 0) {
45       int k = j;
46       while (k > 0) {
47         sum += BITree[i][k]; // accumulate the sum
48         k -= k & (-k); // move column index to parent node
49       }
50       i -= i & (-i);   // move row index to parent node
51     }
52     return sum;
53   }
54 
55   public int sumRegion(int i1, int j1, int i2, int j2) {
56     return getSum(i2, j2) - getSum(i1-1, j2) - getSum(i2, j1-1) + getSum(i1-1, j1-1);
57   }
58 }
59 
60 
61 // Your NumMatrix object will be instantiated and called as such:
62 // NumMatrix numMatrix = new NumMatrix(matrix);
63 // numMatrix.sumRegion(0, 1, 2, 3);
64 // numMatrix.update(1, 1, 10);
65 // numMatrix.sumRegion(1, 2, 3, 4);

 

Introduction from GeeksforGeeks:

We have an array arr[0 . . . n-1]. We should be able to
1 Find the sum of first i elements.
2 Update value of a specified element of the array arr[i] = x where 0 <= i <= n-1.

A simple solution is to run a loop from 0 to i-1 and calculate sum of elements. To update a value, simply do arr[i] = x. The first operation takes O(n) time and second operation takes O(1) time. Another simple solution is to create another array and store sum from start to i at the i’th index in this array. Sum of a given range can now be calculated in O(1) time, but update operation takes O(n) time now. This works well if the number of query operations are large and very few updates.

Can we perform both the operations in O(log n) time once given the array? 
One Efficient Solution is to use Segment Tree that does both operations in O(Logn) time.

Using Binary Indexed Tree, we can do both tasks in O(Logn) time. The advantages of Binary Indexed Tree over Segment are, requires less space and very easy to implement..

Representation
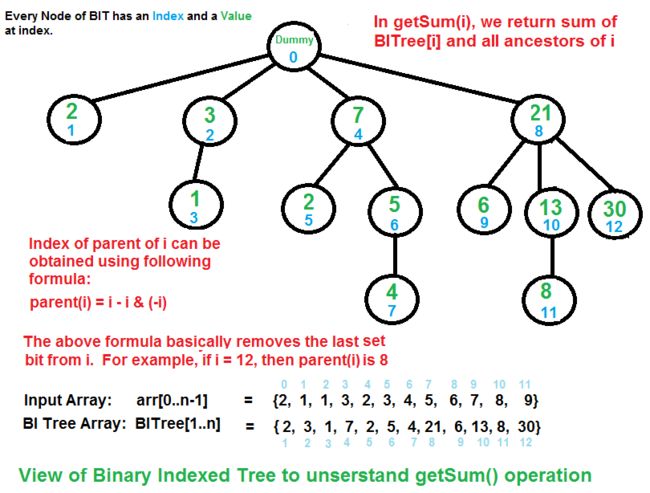
Binary Indexed Tree is represented as an array. Let the array be BITree[]. Each node of Binary Indexed Tree stores sum of some elements of given array. Size of Binary Indexed Tree is equal to n where n is size of input array. In the below code, we have used size as n+1 for ease of implementation.(index 0 is a dummy node)

Construction
We construct the Binary Indexed Tree by first initializing all values in BITree[] as 0. Then we call update() operation for all indexes to store actual sums, update is discussed below.

 

Operations

getSum(index): Returns sum of arr[0..index]
// Returns sum of arr[0..index] using BITree[0..n].  It assumes that
// BITree[] is constructed for given array arr[0..n-1]
1) Initialize sum as 0 and index as index+1.
2) Do following while index is greater than 0.
...a) Add BITree[index] to sum
...b) Go to parent of BITree[index].  Parent can be obtained by removing
     the last set bit from index, i.e., index = index - (index & (-index))
3) Return sum.

The above diagram demonstrates working of getSum(). Following are some important observations.

Node at index 0 is a dummy node.

A node at index y is parent of a node at index x, iff y can be obtained by removing last set bit from binary representation of x.

A child x of a node y stores sum of elements from of y(exclusive y) and of x(inclusive x).

 

update(index, val): Updates BIT for operation arr[index] += val
// Note that arr[] is not changed here.  It changes
// only BI Tree for the already made change in arr[].
1) Initialize index as index+1.
2) Do following while index is smaller than or equal to n.
...a) Add value to BITree[index]
...b) Go to next node of BITree[index].  Next node can be obtained by i.e., index = index + (index & (-index))