DFS应用——找出无向图的割点
【0】README
0.1) 本文总结于 数据结构与算法分析, 源代码均为原创, 旨在 理解 "DFS应用于找割点" 的idea 并用源代码加以实现;
0.2) 必须要事先 做个specification的是:对于给定图的除开起始vertex的那些 vertexes,都可以通过我们的 rules(见下文)找出割点,即对于根(start),我们需要做个special 的test,参见main函数中最后的源码;
【1】 无向图割点相关
1.1)割点定义(articulate point): 如果一个图不是双连通的, 那么将其删除后图将不再连通的那些顶点叫做割点;
1.2)双连通性定义: 如果一个连通的无向图中的任一顶点删除之后, 剩下的图仍然是连通的, 那么这样的无向连通图就是 双连通的;
1.3)看个荔枝: 如果节点是 路由器或者交换机 的话, 边是网络链路, 那么若有一台 路由器或者交换机 出故障而不能运行, 则网络并不会受到影响的;
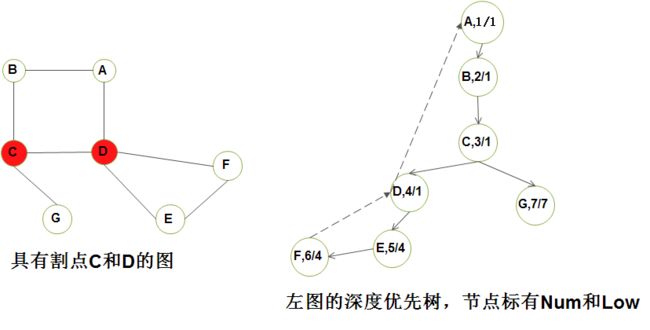
【2】深度优先搜索提供一种找出连通图中的所有割点的线性时间算法
2.1)首先, 从图中任一顶点开始, 执行深度优先搜索并在顶点被访问时给它们编号, 对于每一个顶点,我们称其为先序编号 Num(v) (注:在源代码中,vertexIndex 表示Num的含义,下文不再累述);
2.2)然后, 对于深度优先搜索生成树上的每一个顶点v, 计算编号最低的顶点, 我们称之为 Low(v),该点从v 开始, 通过树的零条或多条边且可能还有一条背向边而达到 (注:在源代码中,vertexLow 表示Low的含义,下文不再累述);
Attention)右上图中的深度优先搜索树首先指出先序编号,然后指出上述法则下可达到的最低编号顶点;
2.3)从A、B、C开始的可达到最低编号顶点为1(A), 因为它们都能够通过树的边到D, 然后再由一条背向边回到A;
2.4)我们可以通过对该深度优先生成树执行一次后序遍历有效地算出 Low, 根据low的定义,可知Low(v)是:
- (1) Num(v) +
- (2) 所有背向边(v, w)中的最低Num(w) +
- (3) 树的所有边(v, w)中的最低Low(w), 以上三者中 的最小者;
- 对以上规则的分析: 第一个条件是不选取边; 第二种方法是不选取树的边 而是选取一条背向边;第三种方法则是选择树的某些边以及可能还有一条背向边;
Attention)
- A1)由于我们需要对v 的所有儿子计算出 Low 值后才能计算Low(v) , 因此这是一个后序遍历;
- A2)对于任一条边(v, w), 我们只要检查Num(v)和 Num(w)就可以知道它是树的一条边还是一条背向边(因为如果是深度优先树的边, Num(v) < Num(w), 因为v比w先被访问到, 而如果是背向边,Num(v) >Num(w)的 );
- A3)因此, Low(v) 容易计算: 我们仅仅需要扫描v 的邻接表,应用适当 的法则,并记住最小值。 所有的计算花费 O(|E| + |V|);
【3】剩下要做的就是利用 这些信息找出所有的割点。
3.1)对于根(见本文README部分):根是割点当且仅当它有多于一个的儿子(根至少要有两个儿子),因为如果它有两个儿子, 那么删除根则使得节点不连通而分布在不同的子树上;如果根只有一个儿子, 那么除去该根只不过是断离该根。
3.2)对于任何其他顶点v: 它是割点当且仅当它有某个儿子w 使得Low(w)>= Num(v); (注意, 这个条件在根处总是满足的; 因此,需要进行特别的测试)(干货)
【4】source code + printing results
4.1)download source code: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter9/p242_dfs_findArticulation
4.2)source code at a glance:(for complete code , please click the given link above)
- 4.2.1) 找割点的函数
// "find the articulation point from the given graph"
void findArticulate(Vertex vertex, int depth)
{
int i;
AdjTable temp;
Vertex adjVertex;
visited[vertex] = 1; // update visited status of vertex
vertexIndex[vertex] = counter++; // evaluating vertex index with counter
vertexLow[vertex] = vertexIndex[vertex]; // the 1st rule: evaluating vertex low with counter
temp = adj[vertex];
while(temp->next)
{
adjVertex = temp->next->vertex;
if(visited[adjVertex]) // judge whether the adjVertes was visited before
{
if(vertexIndex[vertex] > vertexIndex[adjVertex] && parent[vertex] != adjVertex)
{
parent[adjVertex] = vertex; // building back side, attention of condition of building back side above
//ex vertex= 3, adjVertex = 0
// just for printing effect
for(i = 0; i < depth; i++)
printf(" ");
printf("vertex[%c]->vertex[%c] (backside) \n", flag[vertex], flag[adjVertex]);
// only if there's a backside, we apply the 2rd rule into the graph
vertexLow[vertex] = minimum(vertexLow[vertex], vertexIndex[adjVertex]); // the 2rd rule: find lowest vertexIndex[w] among all edges(v, w)
}
}
// if(!visited[adjVertex])
// there's the case no backside, and if condition sentences refers to case of backside
else
{
parent[adjVertex] = vertex;
// just for printing effect
for(i = 0; i < depth; i++)
printf(" ");
printf("vertex[%c]->vertex[%c] (building edge)\n", flag[vertex], flag[adjVertex]);
findArticulate(adjVertex, depth+1);
if(vertex != start) // judge whether the vertex is the start (root) or not
if(vertexLow[adjVertex] >= vertexIndex[vertex])
printf("\n\t vertex[%c] proves to be an articulation point !", flag[vertex]);
vertexLow[vertex] = minimum(vertexLow[vertex], vertexLow[adjVertex]); // the 3rd rule: find lowest verdexLow[w] among all edges(v, w)
}
temp = temp->next;
}
} - 4.2.2) 判断start顶点是否是割点的函数
int isStartArticulation()
{
int i;
AdjTable temp;
Vertex adjVertex;
temp = adj[start];
while(temp->next)
{
adjVertex = temp->next->vertex;
if(adjVertex == start)
{
temp = temp->next;
continue;
}
dfs(adjVertex, 1);
for(i=0; i<size; i++)
if(visited[i] != 1) // "refers that the start vertex is the articulation point"
return 1;
temp = temp->next;
}
return 0;
}