Union-Find(并查集): Union-Find Application
Union-find 可以应用在很多方面
之前我们看到了union-find在dynamic connectivity上的应用,接下来介绍它在percolation上的应用。
union-find在Kruskal's minumum spanning tree algorithm(一种图像处理算法)上也有应用(之后会介绍)
Percolation问题
percolate问题是很多物理系统的模型。
白色代表是open site,黑色是blocked site。如果从顶到底可以由open sites相连,则它是percolates,否则不是percolate.
percolation model的一些例子
可以用来判断一个物体是否导电,可以判断一个物体是否渗水,还可以用来判断两个人之间是否有联系。
medium vacancy是否percolation
如果vacancy的概率是low(0.4),则由上图可知,它是not percolate
如果vacancy的概率是medium(0.6),则由上图可知,它可能percolate,也可能不会。
如果vacancy的概率是high(0.8),则由上图可知,它是percolate.
那么当我们遇到medium vacancy时,我们怎么才能知道是否是percolate呢?
Percolation phase transition(相变):如何找到这个threshold P*(临界点)
Monte Carlo simulation:有计算机来解决找到这个threshold P*的问题
初使化时都是blocked,随机的使site变成open,直到它成为percolation时的vacancy比率,即为p*
我们可以在计算机上对这个模拟运行很多次来计算,找到这个P*在数学上是不可以实现的,但是在计算机上却是可以实现
用dynamic connectivity来估计P*
看上面的一排与底下的一排是否相连,但是这样做并不好,因为这样会运行n2次connected来判断,导致运行非常慢,那么我们该怎么办呢?
如右图所示,我们创建两个虚拟的site(virtual top site和virtual bottom site),这样只需要判断top site与bottom site是否相连就可以了。(只需要运行一次connected())
用dynamic connectivity来估计P* :怎么model opening a new site
当opening a new site时,将它与邻近的也是open的site的相连(最多4个),通过调用union操作来执行
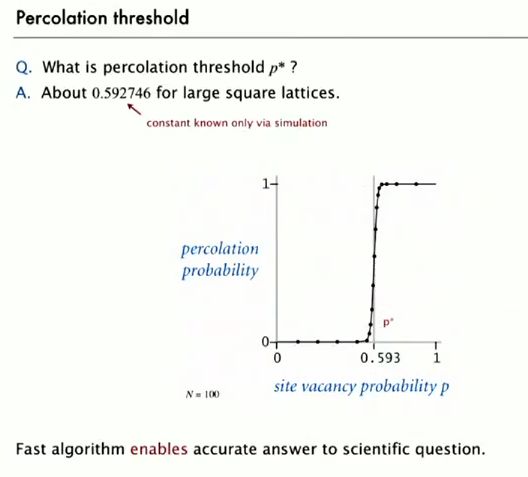
Percolation threshold
这样我们通过运行这个simulation来计算出这个P*(这在数学上是不可能计算出来的),我们只有通过fast的算法才能实现这个问题(因为这类问题的N与M一般来说都很大)
总结
通过以上这些我们可以看到解决问题的基本步骤,首先我们会对问题进行建模,将问题抽象出来;
然后找到算法来实现它,之前介绍的quick-find 与quick-union算法都不是好的算法(对于解决huge problem来说),故我们不断的通过迭代来寻找高效的算法,即weighted quick-union with path compression