寒假集训日志(二)——最小生成树,拓扑排序,欧拉回路,连通路
今天学的内容挺多的。
(一)首先说最小生成树,两种算法:
1.Kruskal算法( 将边排序,然后再选,关键在于检查是否连通,使用并查集)
2.Prim算法(使用点集,有点类似与最短路的算法)
第一题是并查集算法的使用:
Description
Input
Output
Sample Input
100 4 2 1 2 5 10 13 11 12 14 2 0 1 2 99 2 200 2 1 5 5 1 2 3 4 5 1 0 0 0
Sample Output
4 1 1
我的代码:
#include<iostream> #include<cstdio> #include<algorithm> #include<queue> #include<vector> #include<cstring> using namespace std; const int MAXN = 30010; int fa[MAXN]; int Find ( int x){ if( fa[x] == x) return x; else return fa[x] = Find( fa[x] ); } void Union ( int u , int v){ int k = Find ( u); int g = Find ( v); fa[g] = k ; } int main(){ int n, m; while(cin>>n>>m && (n!=0 || m!=0)){ for( int i = 0 ; i<n; ++i){ fa[i] = i ; } for( int i = 0 ; i < m ; ++i){ int len; cin>>len ; int before ; int now; for( int j= 0 ; j<len ; ++j){ if( j== 0 ) cin>>now ; else{ before = now ; cin>> now ; Union ( before , now); } } //输入合并完成 } int flag = Find(0) ; int ans = 0 ; for( int i = 0 ; i < n; ++i){ if(Find(i) == flag ) ans ++; } cout<<ans<<endl; } return 0 ; }
此处要注意的是,最后的判断步骤每个都要查到祖宗(使用find) 不能简单的查老爸;
另外,find的复杂度很小,据学长说几乎可以视为o(1);
Description
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是"1 X Y",表示X和Y是同类。
第二种说法是"2 X Y",表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N(1 <= N <= 50,000)和K句话(0 <= K <= 100,000),输出假话的总数。
Input
以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。
若D=1,则表示X和Y是同类。
若D=2,则表示X吃Y。
Output
Sample Input
100 7 1 101 1 2 1 2 2 2 3 2 3 3 1 1 3 2 3 1 1 5 5
Sample Output
3
#include<iostream> #include<cstdio> #include<algorithm> #include<queue> #include<vector> #include<cstring> using namespace std; typedef long long LL; const int maxN = 50010; int fa[maxN], re[maxN]; int Find(int x){ if(x!=fa[x]){ int t = Find(fa[x]); re[x] = (re[x] + re[fa[x]])%3; fa[x] = t; } return fa[x]; } bool Union(int d, int x, int y){ int fx = Find(x), fy = Find(y); if(fx == fy){ if( (re[y]-re[x]+3)%3!=d ) return true; else return false; } fa[fy] = fx; re[fy] = (re[x] - re[y] + d + 3)%3; return false; } int main() { int n,k; scanf("%d%d", &n, &k); int a, b, c, ans=0; for(int i=0 ;i<maxN;++i){ re[i]=0; fa[i] = i; } while(k--){ scanf("%d%d%d", &a, &b, &c); if(b>n||c>n) ans++; else if(a==2 && b==c) ans++; else if(Union(a-1,b,c)) ans++; } printf("%d\n", ans); return 0; }
Description
Farmer John ordered a high speed connection for his farm and is going to share his connectivity with the other farmers. To minimize cost, he wants to lay the minimum amount of optical fiber to connect his farm to all the other farms.
Given a list of how much fiber it takes to connect each pair of farms, you must find the minimum amount of fiber needed to connect them all together. Each farm must connect to some other farm such that a packet can flow from any one farm to any other farm.
The distance between any two farms will not exceed 100,000.
Input
Output
Sample Input
4 0 4 9 21 4 0 8 17 9 8 0 16 21 17 16 0
Sample Output
28
我的代码:
#include<iostream> #include<cstdio> #include<algorithm> #include<queue> using namespace std; const int MAXN = 110; const int INF = 10e7; int cost[MAXN][MAXN]; bool vis[MAXN]; int lowest[MAXN]; int ans; int main() { int T; while( cin>>T ){ for( int i = 1 ; i<=T ; ++i) for( int j = 1; j<=T ; ++j) cin>>cost[i][j] ; ans = 0; for( int i = 1 ; i<=T ; ++i){ vis[i]= 0; } vis [1] = 1 ; for( int i = 1 ; i<= T ; ++i){ lowest[i] = cost[1][i] ; } for( int i = 1 ; i<= T ; ++i){ int k=-1 ; int minn = INF; for( int j = 1 ; j<= T ; ++j){ if( !vis[j] && lowest[j] < minn){ minn = lowest[j] ; k = j; } } if( k==-1 ) break; vis [k] = 1; ans += lowest[k]; for( int j = 1; j<= T ; ++j){ if( !vis[j] && cost[k][j] < lowest[j]) lowest[j] = cost[k][j]; } } cout<< ans <<endl; } return 0; }
最短路,模板题。
(二)拓扑排序
思想还是挺简单的,首先得知道入度,出度这两个概念。
总的思想就是将入度为零的放在前面(或将出度为零的放在后面),因为没有了约束,然后再删掉边(就是直接减少与之相邻的度),如果又出现了入度为零的就丢到后面,如此循环。
Description
现在有n个人,从1标号到n。同时有一些奇怪的约束条件,每个都形如:a必须在b之前。
同时,社会是不平等的,这些人有的穷有的富。1号最富,2号第二富,以此类推。有钱人就贿赂负责人,所以他们有一些好处。
负责人现在可以安排大家排队的顺序,由于收了好处,所以他要让1号尽量靠前,如果此时还有多种情况,就再让2号尽量靠前,如果还有多种情况,就让3号尽量靠前,以此类推。
那么你就要安排大家的顺序。我们保证一定有解。
Input
然后对于每个测试数据,第一行有两个整数n(1 <= n <= 30000)和m(1 <= m <= 100000),分别表示人数和约束的个数。
然后m行,每行两个整数a和b,表示有一个约束a号必须在b号之前。a和b必然不同。
Output
Sample Input
Sample Output
#include<iostream> #include<cstdio> #include<algorithm> #include<queue> #include<vector> #include<cstring> using namespace std; const int maxPoint = 30010; vector <int> Edge[maxPoint]; int indgree[maxPoint]; int main(){ int T; scanf("%d",&T); while( T-- ){ int n, m; int a , b; scanf("%d %d",&n,&m); memset( indgree , 0 , sizeof(indgree)); for( int i = 1 ; i<= n ; ++i){ Edge[i].clear(); } for( int i= 1 ; i<=m ;++i){ scanf("%d %d",&a,&b); Edge[b].push_back(a); indgree[a] ++; } priority_queue <int> q; for( int i = 1 ; i<=n; ++i){ if( indgree[i] == 0) q.push(i); } vector <int> res ; while( !q.empty()){ int t = q.top() ; res.push_back(t); q.pop(); for( int i = 0 ; i< Edge[t].size() ; ++i){ int x = Edge[t][i] ; indgree[x] --; if(indgree[x] == 0 ) { q.push(x); } } } for(int i = res.size() -1 ; i>= 0 ; --i){ if( i == 0) printf("%d", res[i] ); else printf("%d ", res[i]); } puts(""); } return 0; }
另外,此题的输入次数过多,用cin会超时。
(三)欧拉回路(转自师兄WhyWhy:http://www.cnblogs.com/whywhy/p/5067085.html)
问题:
求一个无向图的一条欧拉路?也就是是否可以一笔画完?
先判断图是否存在欧拉路,不存在直接返回。根据欧拉的定理:如果一个无向图有三个或者三个以上的点的度数是奇数,就没有欧拉路。
先找到degree为奇数的一个点(不存在的话就任意点)作为开始点,进行DFS,每次走过一条边之后就删除这条边。然后当某个点无路可走的时候,把这个点加入答案数组。
最后答案数组反向就是答案。
伪代码如下:
1 vector <int> ans; 2 3 void dfs(int u) { 4 if(u没有路可以继续下去) ans.push_back(u); 5 else { 6 for(e 是 u 出发的边) { 7 delete e; 8 dfs(e.to); 9 } 10 } 11 } 12 13 void getEuler() { 14 int start; 15 for(start=1;start<=N;++start) 16 if(degree(start)%2==1) 17 break; 18 if(start==N+1) start=1; 19 20 dfs(start); 21 ans.reverse(); // ans反向。 22 }
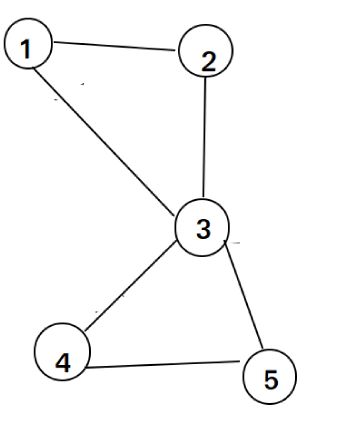
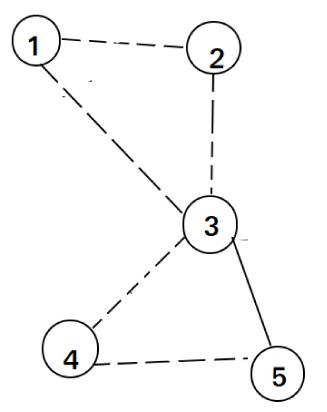
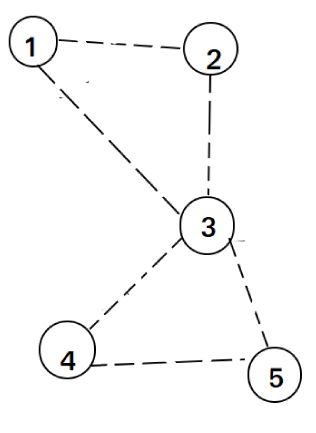
例图如下:
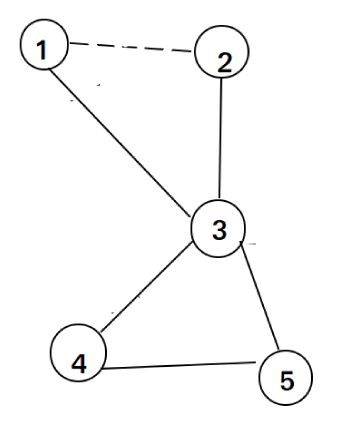
从1开始dfs,找到1-2的边,删除,dfs 点2 然后找到边2-3,删除,dfs 点3
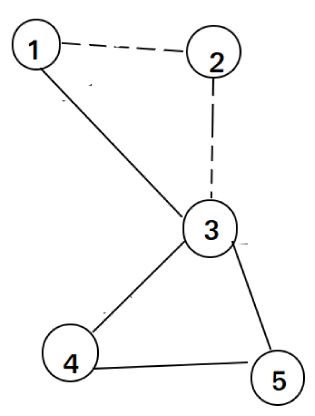
然后找到边1-3,删除,dfs 点1。 这时dfs 点1无路可走,把1加入ans。然后回溯到3, 然后找到边4-5,删除,dfs 点5。
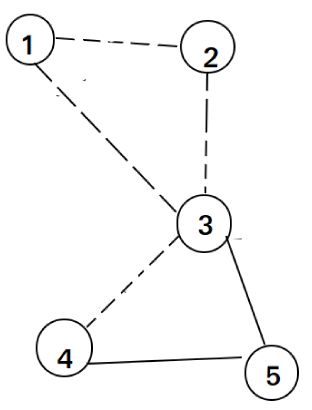
找到边3-4,删除,dfs 点4。
然后找到边5-3,删除,dfs 点3 然后3无路可走,加入ans,回溯到5,然后5无路可走,加入ans,回溯到4,然后4无路可走,加入ans,回溯到3,然后3无
路可走,加入ans,回溯到2,然后2无路可走,加入ans,回溯到1,然后1无路可走,加入ans。
这时ans数组是 1,3,5,4,3,2,1。
倒序的话就是一条欧拉路。
至于正确性的证明,严密的证明不会,但是如果一个点边很少的话一定要尽量往后被访问,不然进去就出不来了。所以这算是半个贪心策略,嗯。
懂是懂了。。。然而不会做题
Description
While dad was at work, a little girl Tanya decided to play with dad's password to his secret database. Dad's password is a string consisting of n + 2 characters. She has written all the possible n three-letter continuous substrings of the password on pieces of paper, one for each piece of paper, and threw the password out. Each three-letter substring was written the number of times it occurred in the password. Thus, Tanya ended up with n pieces of paper.
Then Tanya realized that dad will be upset to learn about her game and decided to restore the password or at least any string corresponding to the final set of three-letter strings. You have to help her in this difficult task. We know that dad's password consisted of lowercase and uppercase letters of the Latin alphabet and digits. Uppercase and lowercase letters of the Latin alphabet are considered distinct.
Input
The first line contains integer n (1 ≤ n ≤ 2·105), the number of three-letter substrings Tanya got.
Next n lines contain three letters each, forming the substring of dad's password. Each character in the input is a lowercase or uppercase Latin letter or a digit.
Output
If Tanya made a mistake somewhere during the game and the strings that correspond to the given set of substrings don't exist, print "NO".
If it is possible to restore the string that corresponds to given set of substrings, print "YES", and then print any suitable password option.
Sample Input
5
aca
aba
aba
cab
bac
YES
abacaba
4
abc
bCb
cb1
b13
NO
7
aaa
aaa
aaa
aaa
aaa
aaa
aaa
YES
aaaaaaaaa
//第二天做出来了,year~~~,要注意一下此题如何复原字符串的 #include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> #include<vector> typedef long long LL; using namespace std; const int MAXN = 200010; vector <int> edge[MAXN]; int in[MAXN]; int out[MAXN]; int vis[MAXN]; string ans; void dfs ( int x){ while( vis[x] < edge[x].size()){ dfs( edge[x][ vis[x]++ ] ); } ans +=(char)(x%200); } int main() { int n; cin>>n; char str[10]; memset( in , 0 , sizeof(in)); memset( out, 0 , sizeof( out)); memset( vis, 0 , sizeof( vis)); int start ; for ( int i = 0 ; i< n; ++i){ scanf("%s", str); int u = str[0] *200 + str[1] ; int v = str[1] *200 + str[2] ; edge[u].push_back(v); out[u]++; in[v]++; start = u; } int flag1 = 0 , flag2= 0; for( int i = 0 ; i < 100000 ; ++i){ int d = in[i] - out[i] ; if( d== 1) flag1++; else if( d == -1 ){ flag2++; start = i; } else if( d!=0 ){ cout<<"NO"<<endl; return 0; } } if( flag1 > 1 || flag2 > 1) { cout<<"NO"<<endl; return 0; } dfs( start); ans += start / 200 ; reverse( ans.begin() , ans.end()); if( ans.length() == n +2) { cout<<"YES"<<endl; cout<<ans<<endl; } else{ cout<<"NO"<<endl; } return 0; }
(四)连通路
1.Kosaraju 算法(两次DFS,正反一次,更为简单)
2.Tarjan 算法(直接没听懂)
Description
Input
Output
Sample Input
Sample Output
#include<iostream> #include<cstdio> #include<algorithm> #include<queue> #include<vector> #include<cstring> using namespace std; const int MAXN = 10010; vector <int> edge1[MAXN]; vector <int> edge2[MAXN]; vector <int> s; int mark[MAXN]; void dfs1( int x ){ mark[x] = 1; for( int i = 0; i< edge1[x].size() ; ++i){ if( !mark[ edge1[x][i] ] ){ dfs1( edge1[x][i] ); } } s.push_back(x); } void dfs2( int x){ mark[x] = 1; for( int i =0 ; i< edge2[x].size() ; ++i){ if( !mark[ edge2[x][i] ] ){ dfs2( edge2[x][i] ); } } } int main(){ int n, m; while( cin>>n>>m && ( n!=0 || m!= 0 )){ int a, b; s.clear(); s.push_back(0); memset( mark , 0 , sizeof( mark) ); for( int i = 0 ; i<=n; ++i){ edge1[i].clear(); edge2[i].clear(); } for( int i = 0 ; i< m ; ++i){ cin>>a>>b; edge1[a].push_back(b); edge2[b].push_back(a); } for( int i =1 ; i<= n; ++i){ if( !mark[i] ) dfs1(i); } int ans = 0 ; memset( mark , 0 , sizeof( mark) ); for( int i = n ; i>=1 ; --i){ if( !mark[ s[i] ] ){ ans++; dfs2( s[i] ); } } if( ans == 1) cout<<"Yes"<<endl; else cout<<"No"<<endl; } return 0; }
判断是否都连通就是判断他的强连通分量是否为1呗。
今天任务没有完成,第D题没有攻克下来,明天加油。