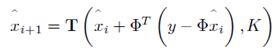浅谈压缩感知(二十九):压缩感知算法之迭代硬阈值(IHT)
主要内容:
1、IHT的算法流程
2、IHT的MATLAB实现
3、二维信号的实验与结果
4、加速的IHT算法实验与结果
一、IHT的算法流程
文献:T. Blumensath and M. Davies, "Iterative Hard Thresholding for Compressed Sensing," 2008.
基本思想:给定一个初始的X0,然后通过以下的阈值公式不断地迭代。
二、IHT的MATLAB实现
function hat_x=cs_iht(y,T_Mat,s_ratio,m) % y=T_Mat*x, T_Mat is n-by-m % y - measurements % T_Mat - combination of random matrix and sparse representation basis % s_ratio - sparsity percentage of original signal % m - size of the original signal % the sparsity is length(y)/4 hat_x_tp=zeros(m,1); % initialization with the size of original s=floor(length(y)*s_ratio); % sparsity u=0.5; % impact factor % T_Mat=T_Mat/sqrt(sum(sum(T_Mat.^2))); % normalizae the whole matrix for times=1:s x_increase=T_Mat'*(y-T_Mat*hat_x_tp); hat_x=hat_x_tp+u*x_increase; [val,pos]=sort(abs(hat_x),'descend'); hat_x(pos(s+1:end))=0; % thresholding, keeping the larges s elements hat_x_tp=hat_x; % update end
三、二维信号的实验与结果
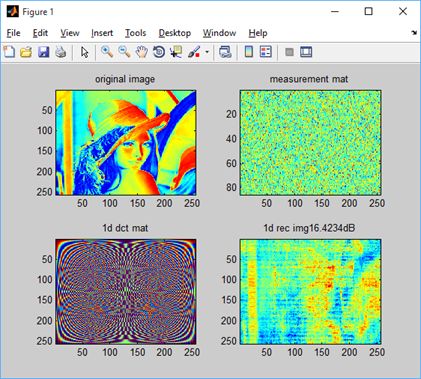
function Demo_CS_IHT() %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % the DCT basis is selected as the sparse representation dictionary % instead of seting the whole image as a vector, I process the image in the % fashion of column-by-column, so as to reduce the complexity. % Author: Chengfu Huo, [email protected], http://home.ustc.edu.cn/~roy % Reference: T. Blumensath and M. Davies, “Iterative Hard Thresholding for % Compressed Sensing,” 2008. %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %------------ read in the image -------------- img=imread('lena.bmp'); % testing image img=double(img); [height,width]=size(img); %------------ form the measurement matrix and base matrix --------------- Phi=randn(floor(height/3),width); % only keep one third of the original data Phi = Phi./repmat(sqrt(sum(Phi.^2,1)),[floor(height/3),1]); % normalize each column mat_dct_1d=zeros(256,256); % building the DCT basis (corresponding to each column) for k=0:1:255 dct_1d=cos([0:1:255]'*k*pi/256); if k>0 dct_1d=dct_1d-mean(dct_1d); end; mat_dct_1d(:,k+1)=dct_1d/norm(dct_1d); end %--------- projection --------- img_cs_1d=Phi*img; % treat each column as a independent signal %-------- recover using iht ------------ sparse_rec_1d=zeros(height,width); Theta_1d=Phi*mat_dct_1d; s_ratio = 0.2; for i=1:width column_rec=cs_iht(img_cs_1d(:,i),Theta_1d,s_ratio,height); sparse_rec_1d(:,i)=column_rec'; % sparse representation end img_rec_1d=mat_dct_1d*sparse_rec_1d; % inverse transform %------------ show the results -------------------- figure(1) % subplot(2,2,1),imagesc(img),title('original image') subplot(2,2,1),imshow(img,[]),title('original image') subplot(2,2,2),imagesc(Phi),title('measurement mat') subplot(2,2,3),imagesc(mat_dct_1d),title('1d dct mat') psnr = 20*log10(255/sqrt(mean((img(:)-img_rec_1d(:)).^2))); % subplot(2,2,4),imagesc(img_rec_1d),title(strcat('1d rec img ',num2str(psnr),'dB')) subplot(2,2,4),imshow(img_rec_1d,[]),title(strcat('1d rec img ',num2str(psnr),'dB')) disp('over') %************************************************************************% function hat_x=cs_iht(y,T_Mat,s_ratio,m) % y=T_Mat*x, T_Mat is n-by-m % y - measurements % T_Mat - combination of random matrix and sparse representation basis % s_ratio - sparsity percentage of original signal % m - size of the original signal % the sparsity is length(y)/4 hat_x_tp=zeros(m,1); % initialization with the size of original s=floor(length(y)*s_ratio); % sparsity u=0.5; % impact factor % T_Mat=T_Mat/sqrt(sum(sum(T_Mat.^2))); % normalizae the whole matrix for times=1:s x_increase=T_Mat'*(y-T_Mat*hat_x_tp); hat_x=hat_x_tp+u*x_increase; [val,pos]=sort(abs(hat_x),'descend'); hat_x(pos(s+1:end))=0; % thresholding, keeping the larges s elements hat_x_tp=hat_x; % update end
结论:实验针对的是图像信号,但算法中运用的是1维的算法,因此实验结果不太理想。(后面提供一个链接,有更好的代码 hard_l0_Mterm.m)
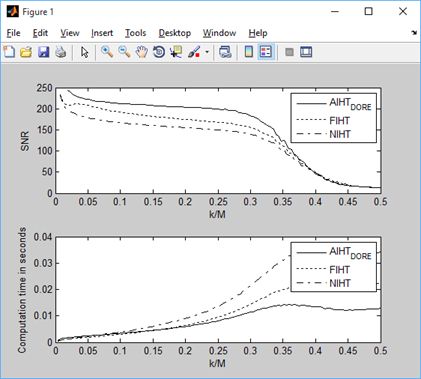
四、加速的IHT算法实验与结果
文献:Blumensath T. Accelerated iterative hard thresholding[J]. Signal Processing, 2012, 92(3): 752-756.
五、相关代码
http://www.personal.soton.ac.uk/tb1m08/sparsify/sparsify.html