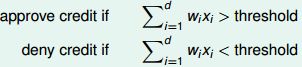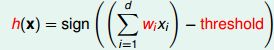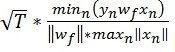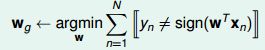NTU-Coursera机器学习:機器學習問題与二元分類
所有内容均来自NTU公开课machine learning Foundations & Techniques中Hsuan-Tien Lin(林軒田)老师的讲解。[1. 機器學習基石 (Machine Learning Foundations) https://www.coursera.org/course/ntumlone ; 2.機器學習技法 (Machine Learning Techniques) https://www.coursera.org/course/ntumltwo]
What is Machine Learning?
From Learning to Machine Learning
Key Essence of Machine Learning
PS: A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.(与Tom M. Mitchell的定义一致). 简而言之,就是我们想要机器在某些方面有提高(如搜索排名的质量,即NDCG提高),就给机器一些数据(用户的点击数据等各种)然后让机器获得某些经验(Learning to rank的一种模型,也就是数学公式)。这里有点需要强调,那就是提高指标,必须要有某种指标可以量化这种提高,这点还是很关键的,工业界做机器学习,首先关注data,其次就是有无成型的measurement,可以使Precision/Recall,也可以是NDCG等
使用Machine Learning 方法的关键
1. 存在有待学习的“隐含模式”
2.该模式不容易准确定义(直接通过程序实现)
3.存在关于该模式的足够数据
其实就三要素:有规律可以学习; 编程很难做到;有能够学习到规律的数据;编程很难做到可以有多种,大部分原因是系统太复杂,很难用Rule-based的东西去解决,例如搜索排名,现在影响排名的因素有超多几百种,不可能去想出这些因素的规则,因此,这时候用机器学习就是恰到好处。特别是移动互联网的今天,用户更容易接触互联网,产生的数据越来越多,那么要找到某些不容易实现的规律,用机器学习就是很好的了,这也是为啥机器学习这么火,其实我学机器学习不仅仅是一种投资(肯定它未来的发展前途),我想做的事情还有一点,就是通过它更深刻的理解人脑的学习过程,提高自己的学习效率和思维能力。
Components of Machine Learning
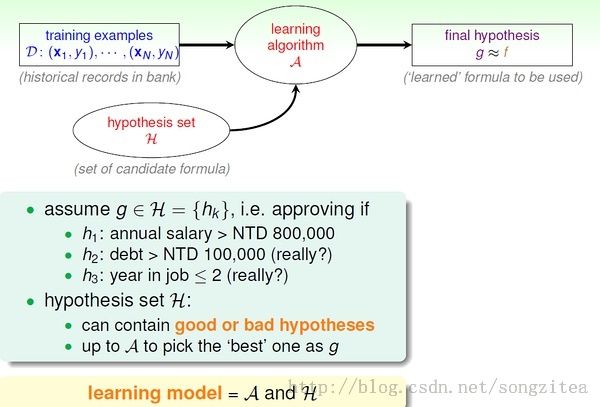
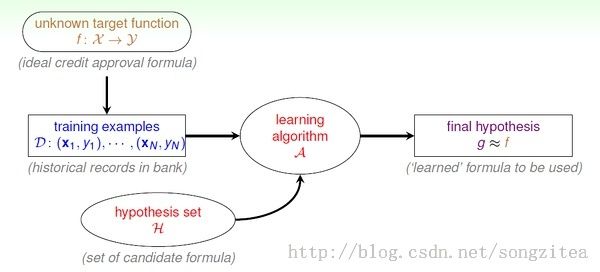
Formalize the Learning Problem
The Learning Model
这里的f 表示理想的方案,g 表示我们求解的用来预测的假设。H 是假设空间。通过算法A, 在假设空间中选择最好的假设作为g。选择标准是 g 近似于 f。
上图增加了"unknown target function f: x->y“, 表示我们认为训练数据D 潜在地是由理想方案f 生成的。机器学习就是通过DATA 来求解近似于f 的假设g。
Machine Learning and Other Fields
Machine Learning vs. Data Mining
数据挖掘是利用(大量的)数据来发现有趣的性质。
- 如果这里的”有趣的性质“刚好和我们要求解的假设相同,那么ML=DM。
- 如果”有趣的性质“和我们要求的假设相关,那么数据挖掘能够帮助机器学习的任务,反过来,机器学习也有可能帮助挖掘(不一定)。
- 传统的数据挖掘关注如果在大规模数据(数据库)上的运算效率。
目前来看,机器学习和数据挖掘重叠越来越多,通常难以分开。
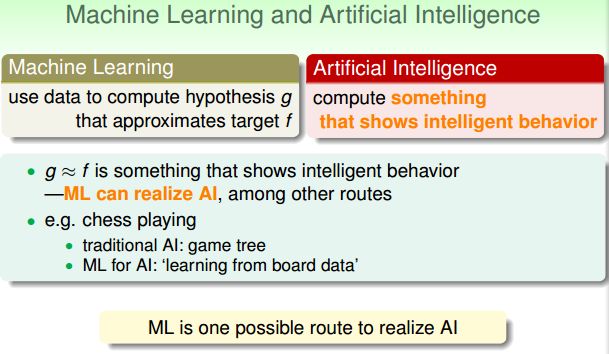
Machine Learning vs. Artificial Intelligence(AI)
人工智能是解决(运算)一些展现人的智能行为的任务。
- 机器学习通常能帮助实现AI。
- AI 不一定通过ML 实现。
例如电脑下棋,可以通过传统的game tree 实现AI 程序;也可以通过机器学习方法(从大量历史下棋数据中学习)来实现。
Machine Learning vs. Statistics
统计学:利用数据来做一些位置过程的推断(推理)。
- 统计学可以帮助实现ML。
- 传统统计学更多关注数学假设的证明,不那么关心运算。
统计学为ML 提供很多方法/工具(tools)。
Perception Hypothesis Set
课程讲述这个算法的总体思路如下(典型的提出问题,分析问题以及解决问题):
- 通过信用卡问题引入PLA;
- 对问题用数学抽象,并得到目标函数;
- 详细解释PLA迭代(学习)过程;
- 证明PLA学习的过程可以收敛并会得到最优解;
- 分析PLA优缺点,并提出克服缺点的一些方法;
这个算法本质上是线性分类器,针对给定的feature vector给出Yes 或者 No的回答.
x = (x1, x2, ..., xd) ---- features. w = (w1, w2, ..., wd) ---- 未知(待求解)的权重.
对于银行是否发送信用卡问题:
perceptron 假设:
这里的思想在于朴素的把从用户信息抽出来的一些feature(年龄等)量化并组成vector,然后乘以一个权重向量,并设定一个阈值,大于这个阈值就表示好,小于表示不好,很明显这个式子的未知变量有两个(实际只有一个): 权重向量 wi, 1<=i<=d; 阈值,下面设为0.做一点小小的变形使得式子更加紧凑.
sign 是取符号函数, sign(x) = 1 if x>0, -1 otherwise向量表示:
感知机(perceptron)是一个线性分类器(linear classifiers)。线性分类器的几何表示:直线、平面、超平面。还有就是从这个模型可以知道,regression model也可以解决classification问题,转化的思想。下面是这个算法的核心,定义了学习目标之后,如何学习?这里的学习是,如何得到最终的直线去区分data?
Perceptron Learning Algorithm (PLA)
Select g from H
Perception Learning Algorithm
这个算法的精髓之处在于如何做到"做错能改",其循环是不断遍历feature vector,找到错误的点(Yn和当前Wt*Xn不符合),然后校正Wt,那么为什么要这样校正?因为这样可以保证Wt越来越靠近perfect直线Wf(ps.暂时没想到正向思维是如何得到这个式子的)课程像大多数课本一样,用逆向思维给予介绍,就是在给定这样能够做的情况下去证明,即证明为什么这样做可以不断接近目标,以及最终一定会停止?
感知机求解(假设空间为无穷多个感知机;注意区分下面的普通乘法和向量内积,内积是省略了向量转置的表示)初始w = 0 (零向量)。
- 第一步:找一个分错的数据(xi, yi), sign(w*xi) != yi;
- 第二步:调整w 的偏差,w = w + yi*xi;
- 循环第一、二步,直到没有任何分类错误, 返回最后得到的w。
实际操作时,寻找下一个错误数据可以按照简单的循环顺序进行(x1, x2, ..., xn);如果遍历了所有数据没有找到任何一个错误,则算法终止。注:也可以预先计算(如随机)一个数据序列作为循环顺序。以上为最简单的PLA 算法。没有解决的一个基本问题是:该算法不一定能停止!
Guarantee of PLA(PLA 算法是否能正常终止)
Linear Separability 分两种情况讨论:数据线性可分;数据线性不可分。这个是比较容易想到的,如果不能用直线去区分data(线性不可分),肯定是解决不了的,所以必须要满足线性可分,其实问题的关键在于如何方便的知道某些数据是否线性可分?这个在课程中目前没有涉及,一种简单的解决方法是画出来,直观的去看,这个我觉得不是好方法。
注意PLA 停止的条件是,对任何数据分类都正确,显然数据线性不可分时PLA 无法停止,这个稍后研究。
我们先讨论线性可分的情况。数据线性可分时,一定存在完美的w(记为wf), 使得所有的(xi, yi), yi = sign(wf*xi).下面证明在数据线性可分时,简单的感知机算法会收敛。另t是表示向量W的更新次数,初始W0=0时,每次遇见错误的数据才会更新.
T次更新之后,
随着T增大,Wf 和WT的夹角越来越小,即W越来越靠近完美向量.而且量向量夹角余弦值不会大于1,可知T 的值有限。由此,我们证明了简单的PLA 算法可以收敛。
Non-Separable Data数据线性不可分
More about PLA
上图中,为了应对Noisy,我们不可能得到完美的直线,那么怎么衡量当前得到的直线能够满足要求呢?凭直觉,我们知道如果当前直线犯错越少越好(对所有data),于是有了下面的改进算法,Pocket PLA,本质上就是在改错的时候多做一步 -- 判断当前改正犯的错是否比之前更小,也就是贪心选择
Learning with Noisy Data
Line with Noise Tolerance
Pocket Algorithm
当数据线性不可分时(存在噪音),简单的PLA 算法显然无法收敛。我们要讨论的是如何得到近似的结果。我们希望尽可能将所有结果做对,即:
寻找wg 是一个NP-hard 问题!只能找到近似解。
与简单PLA 的区别:迭代有限次数(提前设定);随机地寻找分错的数据(而不是循环遍历);只有当新得到的w 比之前得到的最好的wg 还要好时,才更新wg(这里的好指的是分出来的错误更少)。由于计算w 后要和之前的wg 比较错误率来决定是否更新wg, 所以pocket algorithm 比简单的PLA 方法要低效。
最后我们可以得到还不错的结果:wg。
(有错误希望大家指正)
关于Machine Learning更多讨论与交流,敬请关注本博客和新浪微博songzi_tea.