NTU-Coursera机器学习:多類別分类和非线性转换

linear分类模型

在上一讲中，我们了解到线性回归和logistic回归一定程度上都可以用于线性二值分类，因为它们对应的错误衡量(square error, cross-entropy) 都是“0/1 error” 的上界。

三个模型的比较

分析Error Function

本质上讲，线性分类（感知机）、线性回归、logistic回归都属于线性模型，因为它们的核心都是一个线性score 函数：

只是三个model 对其做了不同处理：线性分类对s 取符号；线性回归直接使用s 的值；逻辑斯蒂回归将s 映射到(0,1) 区间。为了更方便地比较三个model，对其error function 做一定处理：

这样，三个error function 都变成只有y*s 这一项“变量”。通过曲线来比较三个error function （注意：cross-entropy 变为以2为底的scaled cross-entropy）

很容易通过比较三个error function 来得到分类的0/1 error 的上界：

这样，我们就理解了通过逻辑斯蒂回归或线性回归进行分类的意义。

优缺点比较

线性分类(PLA)、线性回归、逻辑斯蒂回归的优缺点比较：

• （1）PLA   优点：在数据线性可分时高效且准确。缺点：只有在数据线性可分时才可行，否则需要借助POCKET 算法（没有理论保证）。
• （2）线性回归  优点：最简单的优化（直接利用矩阵运算工具）缺点：y*s 的值较大时，与0/1 error 相差较大(loose bound)。
• （3）logistic回归  优点：比较容易优化（梯度下降）缺点：y*s 是非常小的负数时，与0/1 error 相差较大。
  

实际中，逻辑斯蒂回归用于分类的效果优于线性回归的方法和POCKET 算法。线性回归得到的结果w 有时作为其他几种算法的初值。

随机梯度下降 (Stochastic Gradient Descent)

传统的随机梯度下降更新方法：

每次更新都需要遍历所有data，当数据量太大或者一次无法获取全部数据时，这种方法并不可行。我们希望用更高效的方法解决这个问题，基本思路是：只通过一个随机选取的数据(xn,yn) 来获取“梯度”，以此对w 进行更新。这种优化方法叫做随机梯度下降。

这种方法在统计上的意义是：进行足够多的更新后，平均的随机梯度与平均的真实梯度近似相等。注意：在这种优化方法中，一般设定一个足够大的迭代次数，算法执行这么多的次数时我们就认为已经收敛。（防止不收敛的情况）

多类别分类 (multiclass classification)

与二值分类不同的是，我们的target 有多个类别(>2)。一种直观的解决方法是将其转化为多轮的二值分类问题：任意选择一个类作为+1，其他类都看做-1，在此条件下对原数据进行训练，得到w；经过多轮训练之后，得到多个w。对于某个x，将其分到可能性最大的那个类。（例如逻辑斯蒂回归对于x 属于某个类会有一个概率估计）如果target 是k 个类标签，我们需要k 轮训练，得到k 个w。这种方法叫做One-Versus-All (OVA)：

它的最大缺点是，目标类很多时，每轮训练面对的数据往往非常不平衡(unbalanced)，会严重影响训练准确性。multinomial (‘coupled’) logistic regression 考虑了这个问题，另一种多值分类方法这种方法叫做One-Versus-One(OVO)，对比上面的OVA 方法。基本方法：每轮训练时，任取两个类别，一个作为+1，另一个作为-1，其他类别的数据不考虑，这样，同样用二值分类的方法进行训练；目标类有k个时，需要 k*(k-1)/2 轮训练，得到 k*(k-1)/2 个分类器。预测：对于某个x，用训练得到的 k*(k-1)/2 个分类器分别对其进行预测，哪个类别被预测的次数最多，就把它作为最终结果。即通过“循环赛”的方式来决定哪个“类”是冠军。显然，这种方法的优点是每轮训练面对更少、更平衡的数据，而且可以用任意二值分类方法进行训练；缺点是需要的轮数太多(k*(k-1)/2)，占用更多的存储空间，而且预测也更慢。OVA 和 OVO 方法的思想都很简单，可以作为以后面对多值分类问题时的备选方案，并且可以为我们提供解决问题的思路。

非线性转换

前面的分析都是基于“线性假设“，它的优点是实际中简单有效，而且理论上有VC 维的保证；然而，面对线性不可分的数据时（实际中也有许多这样的例子），线性方法不那么有效。

二次假设

对于下面的例子，线性假设显然不奏效：

我们可以看出，二次曲线（比如圆）可以解决这个问题。接下来就分析如何通过二次曲线假设解决线性方法无法处理的问题，进而推广到多次假设。对于上面的例子，我们可以假设分类器是一个圆心在原点的正圆，圆内的点被分为+1，圆外的被分为-1，于是有：

在上面的式子中，将(0.6, -1, -1) 看做向量w，将(1, x1^2, x2^2) 看做向量z，这个形式和传统的线性假设很像。可以这样理解，原来的x 变量都映射到了z-空间，这样，在x-空间中线性不可分的数据，在z-空间中变得线性可分；然后，我们在新的z-空间中进行线性假设。

在数学上，通过参数w 的取值不同，上面的假设可以得到正圆、椭圆、双曲线、常数分类器，它们的中心都必须在原点。如果想要得到跟一般的二次曲线，如圆心不在原点的圆、斜的椭圆、抛物线等，则需要更一般的二次假设。

非线性转换

进行非线性转换的学习步骤：

这里的非线性转换其实也是特征转换(feature transform)，在特征工程里很常见。

非线性转换的代价

所谓”有得必有失“，将特征转换到高次空间，我们需要付出学习代价（更高的模型复杂度）。x-空间的数据转换到z-空间之后，新的假设中的参数数量也比传统线性假设多了许多：

根据之前分析过的，vc 维约等于自由变量（参数）的数量，所以新假设的dvc 急速变大，也就是模型复杂大大大增加。回顾机器学习前几讲的内容，我们可以有效学习的条件是：（1）Ein(g) 约等于 Eout(g)；（2）Ein(g) 足够小。当模型很简单时（dvc 很小），我们更容易满足（1）而不容易满足（2）；反之，模型很复杂时（dvc很大），更容易满足（2）而不容易满足（1）。看来选择合适复杂度的model 非常trick :-)

假设集

前面我们分析的非线性转换都是多项式转换(polynomial transform)。我们将二次假设记为H2，k次假设记为Hk。显然，高次假设的模型复杂度更高。

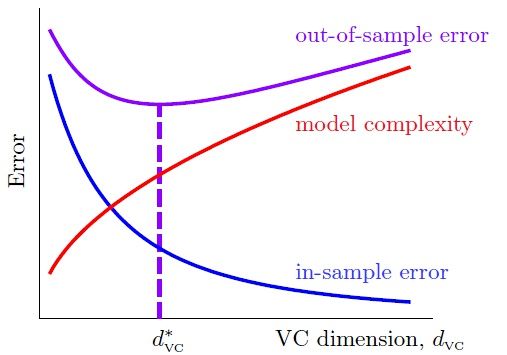
也就是说，高次假设对数据拟合得更充分，Ein 更小；然而，由于付出的模型复杂度代价逐渐增加，Eout 并不是一直随着Ein 减小。

上图我们在前面也见过。实际工作中，通常采用的方法是：先通过最简单的模型（线性模型）去学习数据，如果Ein 很小了，那么我们就认为得到了很有效的模型；否则，转而进行更高次的假设，一旦获得满意的Ein 就停止学习（不再进行更高次的学习）。

关于Machine Learning更多讨论与交流，敬请关注本博客和新浪微博songzi_tea.