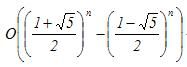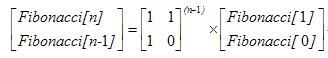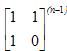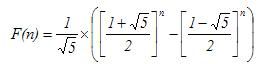程序算法艺术与实践:递归策略之Fibonacci数列
背景:
假定你有一雄一雌一对刚出生的兔子,它们在长到一个月大小时开始交配,在第二月结束时,雌兔子产下另一对兔子,过了一个月后它们也开始繁殖,如此这般持续下去。每只雌兔在开始繁殖时每月都产下一对兔子,假定没有兔子死亡,在一年后总共会有多少对兔子?
在一月底,最初的一对兔子交配,但是还只有1对兔子;在二月底,雌兔产下一对兔子,共有2对兔子;在三月底,最老的雌兔产下第二对兔子,共有3对兔子;在四月底,最老的雌兔产下第三对兔子,两个月前生的雌兔产下一对兔子,共有5对兔子;……如此这般计算下去,兔子对数分别是:1, 1, 2, 3, 5, 8, 13, 21, 34, 55,89, 144, ...看出规律了吗?从第3个数目开始,每个数目都是前面两个数目之和。这就是著名的斐波那契(Fibonacci)数列。
数学表示:
Fibonacci数列的数学表达式就是:
F(n) = F(n-1) + F(n-2)
F(1) = 1 ,F(2) = 1
递归程序1:
Fibonacci数列可以用很直观的二叉递归程序来写,用C++语言的描述如下:
long fib1(int n){
if (n <= 2){ return 1;}
else{ return fib1(n-1) + fib1(n-2);}
}看上去程序的递归使用很恰当,可是在用VC2010的环境下测试n=37的时候用了大约3s,而n=45的时候基本下楼打完饭也看不到结果……显然这种递归的效率太低了!!
递归效率分析:例如,用下面一个测试函数:
long fib1(int n, int* arr){
arr[n]++;
if (n <= 2){ return 1;}
else{return fib1(n-1, arr) + fib1(n-2, arr);}
}
这时,可以得到每个fib(i)被计算的次数:
fib(10) = 1 fib(9) = 1 fib(8) = 2 fib(7) = 3
fib(6) = 5 fib(5) = 8 fib(4) = 13 fib(3) = 21
fib(2) = 34 fib(1) = 55 fib(0) = 34
可见,计算次数呈反向的Fibonacci数列,这显然造成了大量重复计算。我们令T(N)为函数fib(n)的运行时间,当N>=2的时候我们分析可知:
T(N) = T(N-1) + T(N-2) + 2
而fib(n) = fib(n-1) + fib(n-2),所以有T(N) >= fib(n),归纳法证明可得:
fib(N) < (5/3)^N
当N>4时,fib(N)>= (3/2)^N
显然这个O((3/2)^N)是以指数增长的算法,基本上是最坏的情况。
其实,这违反了递归的一个规则:合成效益法则。合成效益法则(Compound interest rule):在求解一个问题的同一实例的时候,切勿在不同的递归调用中做重复性的工作。所以在上面的代码中调用fib(N-1)的时候实际上同时计算了fib(N-2)。这种小的重复计算在递归过程中就会产生巨大的运行时间。
递归程序2:
用一叉递归程序就可以得到近似线性的效率,用C++语言的描述如下:long fib(int n, long a, long b, int count){
if (count == n) return b;
return fib(n, b, a+b, ++count);
}
long fib2(int n){
return fib(n, 0, 1, 1);
}
这种方法虽然是递归了,但是并不直观,而且效率上相比下面的迭代循环并没有优势。
迭代解法:
Fibonacci数列用迭代程序来写也很容易,用C++语言的描述如下://也可以用数组将每次计算的f(n)存储下来,用来下次计算用(空间换时间)
long fib3 (int n){
long x = 0, y = 1;
for (int j = 1; j < n; j++) {
y = x + y;
x = y - x;
}
return y;
}
这时程序的效率显然为O(N),N = 45的时候<1s就能得到结果。
我们将数列写成:
Fibonacci[0] = 0,Fibonacci[1] = 1
Fibonacci[n] = Fibonacci[n-1] + Fibonacci[n-2] (n >= 2)
可以将它写成矩阵乘法形式:
将右边连续的展开就得到:
显然用二分法来求,结合一些面向对象的概念,C++代码如下:
class Matrix{
public:
long matr[2][2];
Matrix(const Matrix&rhs);
Matrix(long a, long b, long c, long d);
Matrix& operator=(const Matrix&);
friend Matrix operator*(const Matrix& lhs, const Matrix& rhs){
Matrix ret(0,0,0,0);
ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];
ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];
ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];
ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];
return ret;
}
};
Matrix::Matrix(long a, long b, long c, long d){
this->matr[0][0] = a;
this->matr[0][1] = b;
this->matr[1][0] = c;
this->matr[1][1] = d;
}
Matrix::Matrix(const Matrix &rhs){
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
}
Matrix& Matrix::operator =(const Matrix &rhs){
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
return *this;
}
Matrix power(const Matrix& m, int n){
if (n == 1) return m;
if (n%2 == 0) return power(m*m, n/2);
else return power(m*m, n/2) * m;
}
long fib4 (int n){
Matrix matrix0(1, 1, 1, 0);
matrix0 = power(matrix0, n-1);
return matrix0.matr[0][0];
}
这时程序的效率为O(log(N))。公式解法:在O(1)的时间就能求得到F(n)了:
注意:其中[x]表示取距离x最近的整数。
用C++写的代码如下:long fib5(int n){
double z = sqrt(5.0);
double x = (1 + z)/2;
double y = (1 - z)/2;
return (pow(x, n) - pow(y, n))/z + 0.5;
}
这个与数学库实现开方和乘方本身效率有关的,我想应该还是在O(log(n))的效率。
总结:
上面给出了5中求解斐波那契数列的方法,用测试程序主函数如下:
int main(){
cout << fib1(45) << endl;
cout << fib2(45) << endl;
cout << fib3(45) << endl;
cout << fib4(45) << endl;
cout << fib5(45) << endl;
return 0;
}函数fib1会等待好久,其它的都能很快得出结果,并且相同为:1134903170。而后面两种只有在n = 1000000000的时候会显示出优势。由于我的程序都没有涉及到高精度,所以要是求大数据的话,可以通过取模来获得结果的后4位来测试效率与正确性。另外斐波那契数列在实际工作中应该用的很少,尤其是当数据n很大的时候(例如:1000000000),所以综合考虑基本普通的非递归O(n)方法就很好了,没有必要用矩阵乘法。
程序全部源码
class Matrix{
public:
long matr[2][2];
Matrix(const Matrix&rhs);
Matrix(long a, long b, long c, long d);
Matrix& operator=(const Matrix&);
friend Matrix operator*(const Matrix& lhs, const Matrix& rhs) {
Matrix ret(0,0,0,0);
ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];
ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];
ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];
ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];
return ret;
}
};
Matrix::Matrix(long a, long b, long c, long d){
this->matr[0][0] = a;
this->matr[0][1] = b;
this->matr[1][0] = c;
this->matr[1][1] = d;
}
Matrix::Matrix(const Matrix &rhs){
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
}
Matrix& Matrix::operator =(const Matrix &rhs){
this->matr[0][0] = rhs.matr[0][0];
this->matr[0][1] = rhs.matr[0][1];
this->matr[1][0] = rhs.matr[1][0];
this->matr[1][1] = rhs.matr[1][1];
return *this;
}
Matrix power(const Matrix& m, int n){
if (n == 1) return m;
if (n%2 == 0) return power(m*m, n/2);
else return power(m*m, n/2) * m;
}
//普通递归
long fib1(int n){
if (n <= 2) { return 1; }
else { return fib1(n-1) + fib1(n-2); }
}
long fib(int n, long a, long b, int count){
if (count == n) return b;
return fib(n, b, a+b, ++count);
}
//一叉递归
long fib2(int n){
return fib(n, 0, 1, 1);
}
//非递归方法O(n)
long fib3 (int n){
long x = 0, y = 1;
for (int j = 1; j < n; j++) {
y = x + y;
x = y - x;
}
return y;
}
//矩阵乘法O(log(n))
long fib4 (int n){
Matrix matrix0(1, 1, 1, 0);
matrix0 = power(matrix0, n-1);
return matrix0.matr[0][0];
}
//公式法O(1)
long fib5(int n){
double z = sqrt(5.0);
double x = (1 + z)/2;
double y = (1 - z)/2;
return (pow(x, n) - pow(y, n))/z + 0.5;
}
int main(){
//n = 45时候fib1()很慢
int n = 10;
cout << fib1(n) << endl;
cout << fib2(n) << endl;
cout << fib3(n) << endl;
cout << fib4(n) << endl;
cout << fib5(n) << endl;
return 0;
}
关于程序算法艺术与实践更多讨论与交流,敬请关注本博客和新浪微博songzi_tea.