GeoHadoop 之 Hilbert 空间填充曲线 Java 实现（一）

       以希尔伯特命名的数学名词多如牛毛，有些连希尔伯特本人都不知道。希尔伯特空间在很多领域都有广泛的应用。由于其强空间聚集特征:① 空间目标的Hilbert 空间排列码相邻, 则空间目标是相邻的；② 空间目标相邻, 则其Hi lbert 空间排列码一般是相邻的。在地理领域，基于Hilbert的空间索引、空间聚类等算法非常多见。今天我们来看下Hilbert是如何来解决空间问题的。首先，来认识下老爷子吧（百度）。更多文章请点击

戴维·希尔伯特（不得不承认老爷子很帅！！！！！！！！！！！！）

       又译大卫·希尔伯特，D.（David Hilbert，1862～1943），德国著名数学家。 他于1900年8月8日在巴黎第二届国际数学家大会上，提出了新世纪数学家应当努力解决的23个数学问题，被认为是20世纪数学的至高点，对这些问题的研究有力推动了20世纪数学的发展，在世界上产生了深远的影响。希尔伯特领导的数学学派是19世纪末20世纪初数学界的一面旗帜，希尔伯特被称为“数学界的无冕之王”，他是天才中的天才。

       我们来看下什么是天才：

     这些图片我估计老爷子都没见过哈。

====================================================================================

先看下的问题：

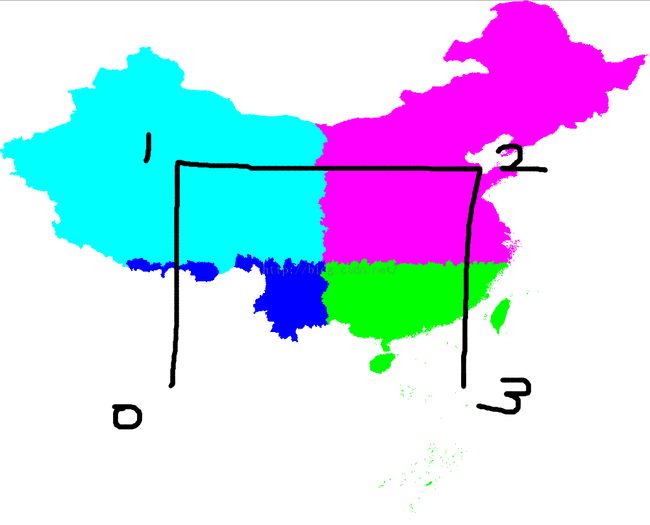
       给你一组空间数据（点，线，面），如何将这些数据按照Hilbert算法进行空间分割。

实现步骤：

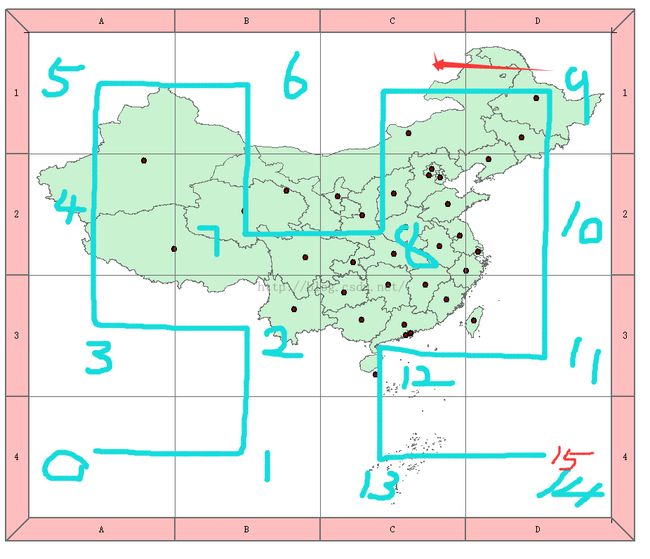
       1、将空间数据进行网格划分，由于Hilbert对应的是2的N次方个网格，所以最好把空间补充为正方形，当然不是正方形也OK；

        2、如果是点要素，直接计算该要素在Hilbert空间中的行列号，更多文章请点击 如果是现，或者面，计算中心点来计算；

        3、将计算好的行列号，以及N传入一下代码中进行实现。返回该要素在Hilbert空间中的位置。

        例如：用户计算输入为 (6,1,3)，那么得到的结果为 61

算了，直接上代码：更多文章请点击

 
public class Hilbert {

	static Logger logger = Logger.getLogger(Hilbert.class);

	public static boolean debug = logger.isDebugEnabled(); 
	
	static Map<String,  Pair[][]> hilbert_map = new HashMap<String,  Pair[][]>(); 
  
	public Hilbert() {
		hilbert_map.put("a", new Pair[][] {
				{ new Pair(0, "d"), new Pair(1, "a") },
				{ new Pair(3, "b"), new Pair(2, "a") } }); 
		hilbert_map.put( "b", new Pair[][] {
				{ new Pair(2, "b"), new Pair(1, "b") },
				{ new Pair(3, "a"), new Pair(0, "c") } });
		hilbert_map.put( "c", new Pair[][] {
				{ new Pair(2, "c"), new Pair(3, "d") },
				{ new Pair(1, "c"), new Pair(0, "b") } });
		hilbert_map.put( "d", new Pair[][] {
				{ new Pair(0, "a"), new Pair(3, "c") },
				{ new Pair(1, "d"), new Pair(2, "d") } }); 
		
	}  
	/**
	 * Our x and y coordinates, then, should be normalized to a range of 0 to
	 * 2order-1
	 * 
	 * @param x
	 * @param y
	 * @param order
	 *            An order 1 curve fills a 2x2 grid, an order 2 curve fills a
	 *            4x4 grid, and so forth.
	 * @return
	 */
	public int xy2d(int x, int y, int order) {
		String current_square = "a";
		int position = 0;
		int quad_x = 0;
		int quad_y = 0;
		int quad_position = 0;
		for (int i = order - 1; i >= 0; i--) {
			position <<= 2;
			quad_x = (x & (1 << i)) > 0 ? 1 : 0;
			quad_y = (y & (1 << i)) > 0 ? 1 : 0;

			System.out.print(quad_x);
			System.out.print('\n');
			System.out.print(quad_y);
			System.out.print('\n');
			
			Pair p = hilbert_map.get(current_square)[quad_x][quad_y];
			quad_position = p.no;
			current_square = p.square;
			position |= quad_position;
		}

		return position;
	}

	static int SCALE_FACTOR = (int) 1e5;
	static int hibert_order = 1;

	static double max_length = 1.5;

	static {
		int Max = (int) (max_length * SCALE_FACTOR);

		int size = 1;
		while (size < Max) {
			size <<= 1;
			hibert_order++;
		}
	}
	
	static class Pair {
		int no = 0;
		String square;

		Pair(int no, String square) {
			this.no = no;
			this.square = square;
		}
	}
}

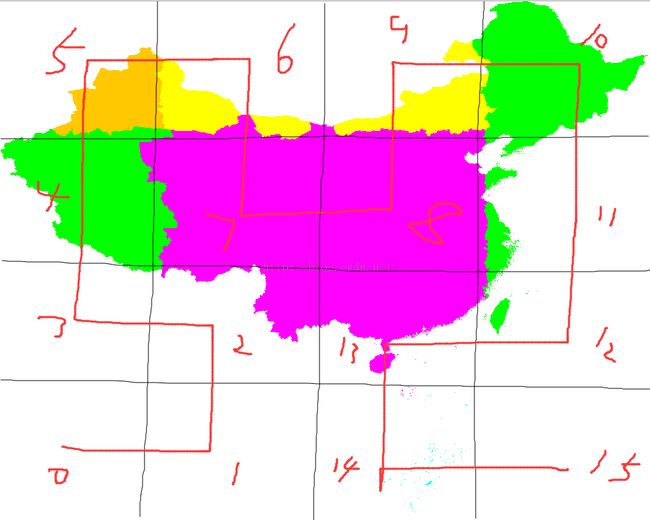
我们来看下具体空间的划分结果：主要从颜色来划分，总共10个颜色。一看就明白了。