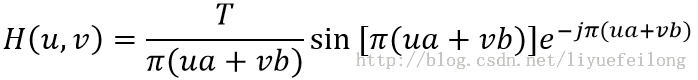参数维纳滤波(Parametric Wiener Filter)



摘   要：本实验主要使用维纳滤波法（又名为最小均方误差滤波）实现图像复原与重建。首先我们通过对一幅图像加入运动污损滤波和高斯噪声，然后从噪声中提取出原始图像信号。在各种估计方法中，维纳滤波是一种最基本的方法，相比起逆滤波，它更适用于从噪声中分离出有用信号的图像。

一、技术论证

1 图像复原与重建

    图像复原技术的主要目的是以预先确定的目标来改善图像。图像复原试图利用退化现象的某种先验知识来复原被退化的图像。因而复原技术是面向退化模型的，并且采用相反的过程进行处理，以便恢复出原图像。

    图1给出了图像退化/复原过程的模型。图像复原处理是建立在图像退化的数学模型基础上的，这个退化数学模型能够反映图像退化的原因。退化过程中可以被模型化为一个退化函数和一个加性噪声项，处理一幅输入图像产生一幅退化图像。给定和关于退化函数的一些知识以及外加噪声项，图像复原的目的是获得关于原始图像的近似估计。通常我们希望这一估计尽可能接近原始输入图像，并且和的信息知道得越多，所得到的就会越接近。

    如果系统H是一个线性、位置不变性的过程，那么在空间域中给出的退化图像可由下式给出：

    其中，是退化函数的空间描述；“*”表示空间卷积。由于空间域上的卷积等同于频域上的乘积，因此，可以把退化图像的模型函数写成等价的频域下的描述：

    公式中各项是式1中相应项的傅里叶变换。本实验使用的退化函数为：

    该函数表示图像在X轴和Y轴分别以给定的速度做匀速直线运动。实验中设定：

图1图像退化/复原过程的模型

2 高斯噪声

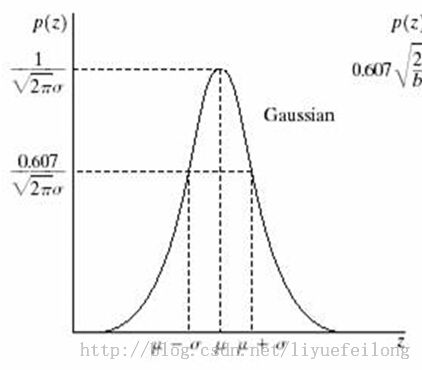
    由于高斯噪声在空间和频域中数学上的易处理性，这种噪声(也称为正态噪声)模型经常被用于实践中。事实上，这种易处理性非常方便，使高斯模型经常用于临界情况下。高斯随机变量z的PDF由下式给出：

图2高斯函数的波形

3 维纳滤波

    维纳滤波综合了退化函数和噪声统计特性两个方面进行复原处理，该方法是建立在认为图像和噪声是随机过程的基础上，目标是找一个未污染图像的估计值，使它们之间的均方误差最小。误差度量由下式给出：

其中是参数的期望值。这里假设噪声和图像不相关，其中一个或另一个有零均值，且估计的灰度级是退化图像灰度级的线性函数。在这些条件下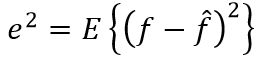，中误差函数的最小值在频域用下列表达式计算：

    这里，我们应用了这样一个事实：一个复数量与它的共轭的乘积等于该复数量幅度的平方。这个结果就是维纳滤波，是N.Wien

er[1942]首次提出的概念。由方括号里边的项所组成的滤波器通常还叫做最小均方误差滤波器，或最小二乘方误差滤波器。式中各项的意义如下：

二、实验结果讨论

    本实验使用冈萨雷斯主编数字图像处理第三版中的素材Fig5.07(a).jpg进行+45度方向，T=1的污损滤波，并对污损图像进行高斯噪声加噪处理。其次，验证维纳滤波法的有效性。从实验结果可以看出维纳滤波对于噪声的复原效果是很好的。

    编写函数gaussian_noise(ima,a,b)产生高斯噪声，其中ima为输入图像，a，b分别是高斯噪声的均值和方差，函数中主要调用了函数randn()，该函数的效果是产生正态分布的随机数或矩阵的函数。要产生一个随机分布的指定均值和方差的矩阵，只需执行以下公式：

    式中(m,n)为图像的尺寸。为了验证函数效果，图3给出均值为0，方差分别为20，200，1000的加性噪声图像。本实验过程中要求生成均值为0、方差为10的高斯噪声。

图3均值为0，方差分别为20，200，1000的加性高斯噪声图像

    编写函数motion(T,a,b)实现图像模糊化，其中使用的核心公式为：

    使用函数进行+45度方向且T=1 的污损滤波，对比MATLAB自带函数的效果，如图4所示，有巨大差异，但图像确实在x和y轴都有同幅度的位移，事实证明只有核心公式还无法做到示例的输出效果。

图4两种函数的运动模糊输出图像

    编写函数实现对运动模糊且存在噪声的图像的重建和复原，其中使用的退化函数为：

    图5和图6分别给出了维纳滤波恢复结果，结果显示维纳滤波能有效重建院图像。而对于图6这种噪声污染严重的图像，使用该滤波方法也能得到有效改善。

图5 图像经过运动模糊、加噪处理（0均值，10方差）和维纳滤波后的效果对比

图6图像经过运动模糊、加噪处理（0均值，100方差）和维纳滤波后的效果对比

以下给出主要部分的MATLAB代码：