算法系列之二十二:离散傅立叶变换之听声音破解电话号码
2012年9月的时候,一个南京的大学生从电视台播放的一段记者采访360总裁周鸿祎的视频中破解了周鸿祎的手机号码,一时间被网络热炒。后来,又听说某人买车的时候使用电话银行付款,结果被人录下声音,破解了银行卡号和密码,导致存款被盗。最近居委会在小区里散发传单,提醒一种新的诈骗方式:电话听音破密码诈骗。各种网络和媒体对这些事情炒作的很热闹,但是趋于两种极端,要么将其说的出神入化,要么将其贬的一钱不值,唯独缺少理性的声音解释一下到底是什么原理。猫猫一直想说,“其实就是离散傅立叶变换(DFT)嘛,至于吗?”,这次就借着这种所谓的新型诈骗方式,一并说道说道。
在动笔写这篇文章之前,猫猫上网Google了一下“电话号码破解”,居然发现某宝上有人叫卖“电话拨号音破解器”,价格从几百到上千大洋的都有,猫猫不说了,只笑笑。本文就准备从理论上解释一些破解电话拨号音的数学原理,看了本文的同学,你有福了,只需要依照本文给出的百十行演示代码,稍加改造,再加上一个麦克风,你就可以拥有自己的“电话拨号音破解器”了,废话少说,现在就开始吧。
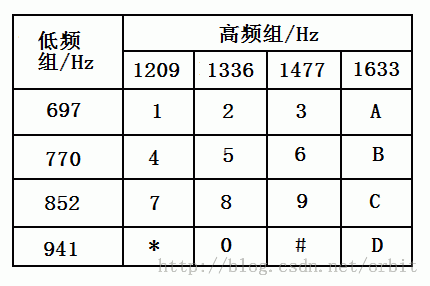
首先要说的是,根据电话拨号音破解电话号码,只适用于使用“双音多频技术(DTMF)”的电话设备,老式的拨号盘电话(脉冲式电话机)您就别试了(估计您也没有这玩意了)。双音多频技术是贝尔实验室的发明,就是将电话机的拨号键盘分成4X4的矩阵,每一行对应一个低频信号,每一列对应一个高频信号,如图(1)所示:
图(1)电话键盘双音频对照表
其中低频信号和高频信号的频率都在人耳可以识别的频率范围之内。打电话拨号的时候,每按下一个键,就产生一个高频信号和低频信号的正弦信号组合,局端的电话交换机从这个组合信号中解出两个频率,就知道是那个按键被按下了。说到这里,您可能已经猜到了,只要从按键音中解析出这两个频率,就能根据上表查出是对应的哪个按键了。
现在该离散傅立叶变换(DFT)隆重登场了!关于离散傅立叶变换算法的来龙去脉,请上网Google之,这里只简单介绍一下它的基本原理,以及它在电话号码破解的过程中能做什么。
傅里叶是一位法国数学家和物理学家的名字,他于1807年在法国科学学会上发表了一篇论文,提到了一个观点:任何连续周期信号可以由一组适当的正弦曲线组合而成,换言之,满足一定条件的连续函数(周期函数)都可以表示成一系列三角函数(正弦和/或余弦函数)或者它们的积分的线性组合形式,这个转换就被称为“傅立叶转换”。一般情况下,若“傅里叶变换”一词的前面未加任何限定语,则指的是“连续傅里叶变换”,与之对应的自然就是“离散傅立叶变换”。事实上,变换原始信号可以是周期的,也可以不是周期的,根据原始信号类型的不同,傅立叶变换可以分成四种形式,分别是“非周期性连续信号傅立叶变换”、“周期性连续信号傅立叶变换”、“非周期性离散信号傅立叶变换”和“周期性离散信号傅立叶变换”,其中“周期性连续信号傅立叶变换”实际上就是傅里叶级数的推广,因为积分其实是一种极限形式的求和算子而已。
一维傅立叶变换的数学意义就是将时域信号转换为频域信号,当然,也存在称为傅立叶逆变换的变换,可以将频域信号转换成时域信号。连续时域信号以及对应的连续傅里叶变换都是连续函数(且是无限长度的时域信号),但是用计算机进行数字处理只能处理有限长度的离散信号,所以必须将原始信号离散化,同时建立对应的离散信号傅里叶变换。所谓的“离散傅里叶变换(Discrete Fourier Transform,缩写为DFT)”,是指傅里叶变换在时域和频域上都以离散的形式呈现。原始信号离散化的过程其实就是以一定的周期对原始信号进行采样的过程,至于如何从连续傅立叶变换推导出离散傅立叶变换,不是本文的重点,您可以Google之。因为离散傅立叶变换计算量相当大,有很多提高效率的算法理论,其中应用最广泛的就是快速傅立叶变换(FFT),关于快速傅立叶变换的理论依据,也不是本文的重点,您可以Google之。总之,您只需要知道,存在一种方法,可以将基于时间轴的时域信号,转换成基于频率的频域信号即可,本文的重点是这种转换的物理意义,以及如何应用这种转换带给我们的结果。
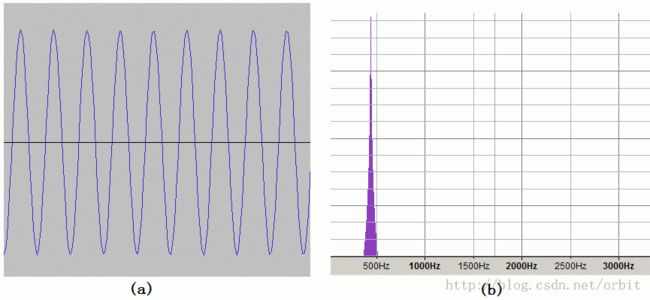
图(2)440Hz正弦波在时域和频域的形态
现在看几个转换对比图,理解一下这种转换的物理意义。首先看图(2),图(2-a)是440Hz的正弦波在时域中的形态,采样率是8000Hz。图(2-b)就是通过离散傅立叶转换后得到的频域中的形态,理想状态下,图(2-b)应该在440Hz处一条直线,其他位置的值都是0,但是受原始信号杂波和转换后的频域分辨率影响,实际显示的是一个呈金字塔形状的图形,不过还是可以明显地看到在440Hz的时候功率(相对强度)值最大,其他位置的值都明显小于440Hz位置的值。
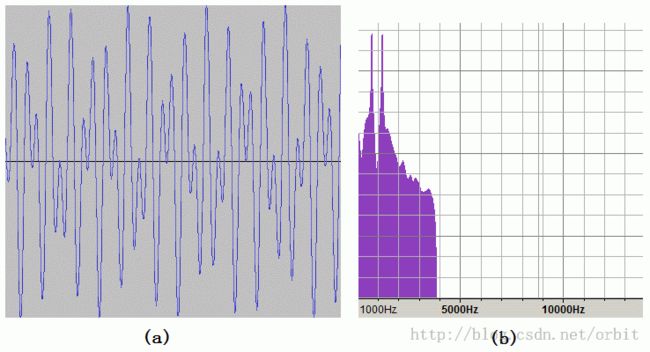
图(3)按键“1”对应的音频在时域和频域的形态
图(3-a)是电话按键“1”对应的音频波形,图(3-b)是离散傅立叶转换后得到的频域形态,虽然受录音杂波影响很大,但是还是可以很明显看到在697Hz和1209Hz位置上,相对能量强度达到了最大值。
前面提到过,原始信号离散化的过程其实就是以一定的周期对原始信号进行采样的过程,这里就提到了一个很重要的参数,就是采样率T。因为这个采样率T决定了转换成频域信号后的分辨率,另外,每次进行转换的时域信号的个数N(也称为离散傅立叶变换的点数)不能小于T,否则无法完整映射到频域信号。实际上,是T和N共同决定了转换后的频域信号的分辨率。以本文要用到的声音信号为例,转换前的数据是每个采样点上的声波的振幅(各个频率叠加后的振幅),横坐标轴是T周期的时间点,纵坐标轴是振幅。转换成频域信号后,横坐标轴就是频率,纵坐标轴就是该频率的产生强度,通过适当的转换,可以理解为该频率的功率。刚才提到,时域信号的采样率T和参与转换的信号点数N决定了频域信号的分辨率,这是因为离散傅立叶转换会将时域信号一对一的转换为频域信号,也就是说,N个时域信号转换后会得到N个频域信号。但是傅立叶转换有个特点,就是时域信号的周期性和频域信号的对称性,所谓频域信号的对称性,是指转换后的N个频域信号在T/2位置呈现轴对称特征,对信号分析有用的实际频域信号点只有N/2 +1个。其中第一个点对应的是0Hz,也就是时域信号中直流分量强度,其他N/2个点分别对应(0,T/2]之间的频率,频率分辨率是T/N。由此可见,增加N可以提高频域信号的分辨率,但是增加N会显著增加每次傅立叶变换的计算量,因此对N的选择需要做一个折衷。
使用离散傅立叶变换进行信号分析的时候,一般都会采用快速傅立叶变换(FFT)算法,网上有很多高效的快速傅立叶变换算法,包括基于实数的快速傅立叶算法,大家可以参考。本文给出的算法是猫猫上学时写的一个快速傅立叶变换算法,输入和输出参数都是复数,算不上高效,但是很简单,只有二十几行代码,适合研究原理使用。另外,这个算法采用原位变换的方式,可以减少傅立叶转换算法使用过程中的数据复制操作。
|
42 /* 43 window = 1 -> hanning window 44 */ 45 bool InitFft(FFT_HANDLE *hfft, int count, int window) 46 { 47 int i; 48 49 hfft->count = count; 50 hfft->win = new float[count]; 51 if(hfft->win == NULL) 52 { 53 return false; 54 } 55 hfft->wt = new COMPLEX[count]; 56 if(hfft->wt == NULL) 57 { 58 delete[] hfft->win; 59 return false; 60 } 61 for(i = 0; i < count; i++) 62 { 63 hfft->win[i] = float(0.50 - 0.50 * cos(2 * M_PI * i / (count - 1))); 64 } 65 for(i = 0; i < count; i++) 66 { 67 float angle = -i * M_PI * 2 / count; 68 hfft->wt[i].re = cos(angle); 69 hfft->wt[i].im = sin(angle); 70 } 71 72 return true; 73 } 74 75 void FFT(FFT_HANDLE *hfft, COMPLEX *TD2FD) 76 { 77 int i,j,k,butterfly,p; 78 79 int power = NumberOfBits(hfft->count); 80 81 /*蝶形运算*/ 82 for(k = 0; k < power; k++) 83 { 84 for(j = 0; j < 1<<k; j++) 85 { 86 butterfly = 1<<(power-k); 87 for(i = 0; i < butterfly/2; i++) 88 { 89 p=j * butterfly; 90 COMPLEX t = TD2FD[i + p] + TD2FD[i + p + butterfly/2]; 91 TD2FD[i + p + butterfly/2] = (TD2FD[i + p] - TD2FD[i + p + butterfly/2]) * hfft->wt[i*(1<<k)]; 92 TD2FD[i + p] = t; 93 } 94 } 95 } 96 97 /*重新排序*/ 98 for(i = 1,j = hfft->count/2;i <= hfft->count-2; i++) 99 { 100 if(i < j) 101 { 102 COMPLEX t = TD2FD[j]; 103 TD2FD[j] = TD2FD[i]; 104 TD2FD[i] = t; 105 } 106 k = hfft->count/2; 107 while(k <= j) 108 { 109 j = j - k; 110 k = k / 2; 111 } 112 j = j + k; 113 } 114 } |
InitFft()函数初始化一个傅立叶转换句柄,包括正/余弦系数表(wt)和窗口系数表(win),count参数是傅立叶转换的点数,就是一次能转换的最大信号个数,windows参数是决定使用什么窗函数,这段代码只支持汉宁窗(hanning window)。有关离散傅立叶变换中窗函数的作用将在后面介绍。FFT()函数就是快速傅立叶变换的实现,TD2FD是个复数数组,每调用一次FFT()函数可以转换count个数据。对于音频数据这样的实数,只需使用COMPLEX结构的实数分量,虚数分量可以置0。COMPLEX数据结构定义如下:
|
8 struct COMPLEX 9 { 10 float re; 11 float im; 12 }; 13 |
COMPLEX数据结构重载了+、-和*运算符,所以FFT()函数的代码看起来很简练。
前文提到过,计算机不能处理无限长度的数据,离散傅立叶变换算法只能对数据一批一批地进行变换,每次只能对限时间长度的信号片段进行分析。具体的做法就是从信号中截取一段时间的片段(比如本文对按键音频文件的分析,从音频文件中读取的数据就可以看做是从无限长度信号中截取的一秒钟音频信号),然后对这个片段的信号数据进行周期延拓处理,得到虚拟的无限长度的信号,再对这个虚拟的无限长度信号进行傅立叶变换。但是信号被按照时间片截取成片段后,其频谱就会发生畸变,这种情况也被称之为频谱能量泄露。
为了减少能量泄露,人们研究了很多截断函数对信号进行截取操作,这些截断函数就被称为窗函数。窗函数w(t)被设计成频带无限的函数,所以即使原始信号是有限带宽信号,被窗函数截取后得到的片段也会变成无限带宽,也就是说,信号经过窗函数处理后,在频域的能量与分布都被扩展了,有效地减少了频谱能量泄露。
不同的窗函数对信号频谱的影响是不一样的,比如最简单的矩形窗,实际上就是对信号不做任何处理,简单地按照时间片段截取一定长度的信号进行处理。本文的演示算法选用了汉宁窗(hanning window),汉宁窗的数学定义如下:
其中R(t)是原始信号,t的范围是 0 <= t < N-1,对于其他范围的值,w(t) = 0。图(4)显示了汉宁窗对信号截取的示意图,以及对频域转换结果的影响,蓝色区域是窗口覆盖的数据部分。汉宁窗的作用是分析带宽加宽,但是降低了频率分辨率,不过拨号音的低频和高频组中,任意两个频率之间的间隔都超过了70Hz,所以牺牲这点分辨率对按键声音的识别没有影响。
图(4)汉宁窗信号截取示意图
使用了窗口,就需要讨论窗口的滑动问题,也就是窗口重叠的处理。用汉宁窗截取的信号片段,可以看出来窗口中部分信号被削弱了(造成衰减),为了抵消部分窗口对信号造成的衰减,各种窗函数都需要对信号进行相应的重叠处理。本文选择的重叠处理方式是选取信号时每次滑动半个窗口位置,使得每个窗口的后半个窗口的衰减在下个窗口的前半个窗口中的到一定的补偿,这个在计算一段时间信号总的功率谱时会有相应的体现。计算一段时域信号的总功率谱的函数代码如下:
|
31 bool PowerSpectrumT(FFT_HANDLE *hfft, short *sampleData, int totalSamples, int channels, float *power) 32 { 33 int i,j; 34 35 for(i = 0; i < hfft->count; i++) 36 power[i] = (float)0.0; 37 38 COMPLEX *inData = new COMPLEX[hfft->count]; 39 if(inData == NULL) 40 return false; 41 42 int procSamples = 0; 43 short *procData = sampleData; 44 while((totalSamples - procSamples) >= hfft->count) 45 { 46 procData = sampleData + procSamples * channels; 47 for(j = 0; j < hfft->count; j++) 48 { 49 SampleDataToComplex(procData, channels, &inData[j]); 50 procData += channels; 51 } 52 procSamples += (hfft->count / 2); /*每次向后移动半个窗口*/ 53 54 FftWindowFunction(hfft, inData); 55 FFT(hfft, inData); 56 57 for(i = 0; i < hfft->count; i++) 58 { 59 power[i] += float(20.0 * log10(sqrt(inData[i].re * inData[i].re + inData[i].im * inData[i].im) / (hfft->count / 2))); 60 } 61 } 62 63 delete[] inData; 64 65 return true; 66 } |
PowerSpectrumT()函数要做的事情很简单,就是每次从采样数据中选择count个,对其进行窗口处理,然后用傅立叶转换得到频域信号,最后计算并累加各个频率的相对功率。处理完一批采样数据后,向后偏移 count/2 个采样数据(相当于滑动半个窗口),重复上述过程,直到剩余的采样数据全部完成为止(剩余数据不足一个窗口时也退出计算)。sampleData参数是采样数据,本文处理的是16位音频数据,因此每个采样的大小是两个字节,totalSamples是总的采样数据的个数,totalSamples必须大于count才能得到有意义的功率频谱。channels是采样数据的声道数,对于有两个声道的立体声采样数据,则取两个声道的平均值做为采样数据进行傅立叶转换。SampleDataToComplex()函数将采样数据赋值给复数对象的实数部分,虚数部分置0,对于双声道,则取左右声道的平均值赋值给复数对象的实数部分,其实现如下:
|
17 static void SampleDataToComplex(short *sampleData, int channels, COMPLEX *cd) 18 { 19 if(channels == 1) 20 { 21 cd->re = float(*sampleData / 32768.0); 22 cd->im = 0.0; 23 } 24 else 25 { 26 cd->re = float(*sampleData + *(sampleData + 1) / 65536.0); 27 cd->im = 0.0; 28 } 29 } |
现在来讲一下对PowerSpectrumT()函数转换结果的处理,PowerSpectrumT()函数的power参数返回最终计算好的功率谱,其分辨率是T/N。每个点对应的频率可使用以下公式计算:
Freq = n * (T / N) (公式2)
以音频信号采样率8000Hz,傅立叶转换的count是2048为例,其频谱分辨率是3.90625Hz,power[0]是频率0的相对功率,也就是直流信号的功率,power[1]是频率3.9Hz对应的相对功率,power[2]是频率7.8Hz对应的相对功率,对应关系以此类推。如果在power[240]处出现频率最大值,则其对应的频率应该是(8000/2048)*240=937Hz。
双音频电话按键音中有两个主频率,因此转换后的power数组中应该存在两个相对极大值,需要从power数组中找出这两个相对极大值。从M个数中选最大的N个数是一个很常见的算法,其主要思想就是维护一个大小是N的有序组,然后从剩下的M-N个数中逐个与有序组中的最小值比较,如果小于有序组中的最小值,则继续比较下一个数,如果大于有序组中的最小值,则替换有序组中的最小值,并对有序组进行适当的变换,使其保持有序。使用堆来维护有序组被认为是最高效的方式,大家有兴趣可以从网上找相关的代码学习。本文设计的从power数组中选出最大的两个值的算法也采用这种思想,但是有序表只有两个元素,因此对有序表的维护不需要复杂的排序处理,如果有序性失效,只要交换两个元素的位置即可,其具体算法如下:
|
290 void ExchangeIndex(int *index, float *power) 291 { 292 if(power[index[1]] > power[index[0]]) 293 { 294 int t = index[0]; 295 index[0] = index[1]; 296 index[1] = t; 297 } 298 } 299 300 void SearchMax2FreqIndex(float *power, int count, int& first, int& second) 301 { 302 int max2Idx[2] = { 0 }; 303 304 ExchangeIndex(max2Idx, power); 305 for(int i = 2; i < count; i++) 306 { 307 if(power[i] > power[max2Idx[1]]) 308 { 309 max2Idx[1] = i; 310 ExchangeIndex(max2Idx, power); 311 } 312 } 313 314 first = min(max2Idx[0], max2Idx[1]); 315 second = max(max2Idx[0], max2Idx[1]); 316 } |
SearchMax2FreqIndex()函数从power数组中选择最大的两个值,并返回它们在power数组中的位置(power数组的下标),并根据频率排序,first总是较小的那个频率的位置,second总是较大的那个频率的位置。根据first和second指示的位置,利用“公式2”就可以计算出两个频率,但是因为频谱分辨率的关系,这两个计算出来的频率不会刚好就是图(1)中所示的标准频率,但是没关系,它们与标准频率差的不多,通过查表就可以确定是哪个标准频率。
至此,所有的核心代码都完成了,创建一个例子试试吧,我的例子很简单,如图(5)所示,就是打开按键音频文件,然后显示是哪个按键。您可以做的更复杂一些,直接从麦克风获得音频数据,实时分析按键声音,这样就可以实时破解电话号码了。
图(5)按键音识别实例程序