算法系列之十一:圆生成算法
输入您的搜索字词 提交搜索表单 |
在平面解析几何中,圆的方程可以描述为(x – x0)2 + (y – y0)2 = R2,其中(x0, y0)是圆心坐标,R是圆的半径,特别的,当(x0, y0)就是坐标中心点时,圆方程可以简化为x2 + y2 = R2。在计算机图形学中,圆和直线一样,也存在在点阵输出设备上显示或输出的问题,因此也需要一套光栅扫描转换算法。为了简化,我们先考虑圆心在原点的圆的生成,对于中心不是原点的圆,可以通过坐标的平移变换获得相应位置的圆。
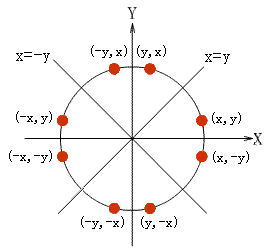
在进行扫描转换之前,需要了解一个圆的特性,就是圆的八分对成性。如图(1)所示:
图(1)圆的八分对称性
圆心位于原点的圆有四条对称轴x = 0、y = 0、x = y和x = -y,若已知圆弧上一点P(x,y),就可以得到其关于四条对称轴的七个对称点:(x, -y)、(-x, y)、(-x, -y)、(y, x)、(y, -x)、(-y, x)、(-y, -x),这种性质称为八分对称性。因此只要能画出八分之一的圆弧,就可以利用对称性的原理得到整个圆。
有几种较容易的方法可以得到圆的扫描转换,首先介绍一下直角坐标法。已知圆方程:x2 + y2 = R2,若取x作为自变量,解出y,得到:
y =
在生成圆时先扫描转换四分之一的圆周,让自变量x从0到R以单位步长增加,在每一步时可解出y,然后调用画点函数即可逐点画出圆。但这样做,由于有乘方和平方根运算,并且都是浮点运算,算法效率不高。而且当x接近R值时(圆心在原点),在圆周上的点(R,0)附近,由于圆的斜率趋于无穷大,因浮点数取整需要四舍五入的缘故,使得圆周上有较大的间隙。接下来介绍一下极坐标法,假设直角坐标系上圆弧上一点P(x,y)与x轴的夹角是θ,则圆的极坐标方程为:
x = Rcosθ
y = Rsinθ
生成圆是利用圆的八分对称性,使自变量θ的取值范围为(0,45°)就可以画出整圆。这个方法涉及三角函数计算和乘法运算,计算量较大。直角坐标法和极坐标法都是效率不高的算法,因此只是作为理论方法存在,在计算机图形学中基本不使用这两种方法生成圆。下面就介绍几种在计算机图形学中比较实用的圆的生成算法。
1、 中点画圆法
首先是中点画圆法,考虑圆心在原点,半径为R的圆在第一象限内的八分之一圆弧,从点(0, R)到点(R/ , R/ )顺时针方向确定这段圆弧。假定某点Pi(xi, yi)已经是该圆弧上最接近实际圆弧的点,那么Pi的下一个点只可能是正右方的P1或右下方的P2两者之一,如图(2)所示:
图(2)中点划线法示例
构造判别函数:
F(x, y)= x2 + y2 – R2
当F(x, y)= 0,表示点在圆上,当F(x, y)> 0,表示点在圆外,当F(x, y)< 0,表示点在圆内。如果M是P1和P2的中点,则M的坐标是(xi + 1, yi – 0.5),当F(xi + 1, yi – 0.5)< 0时,M点在圆内,说明P1点离实际圆弧更近,应该取P1作为圆的下一个点。同理分析,当F(xi + 1, yi – 0.5)> 0时,P2离实际圆弧更近,应取P2作为下一个点。当F(xi + 1, yi – 0.5)= 0时,P1和P2都可以作为圆的下一个点,算法约定取P2作为下一个点。
现在将M点坐标(xi + 1, yi – 0.5)带入判别函数F(x, y),得到判别式d:
d = F(xi + 1, yi – 0.5)= (xi + 1)2 + (yi – 0.5)2 – R2
若d < 0,则取P1为下一个点,此时P1的下一个点的判别式为:
d’ = F(xi + 2, yi – 0.5)= (xi + 2)2 + (yi – 0.5)2 – R2
展开后将d带入可得到判别式的递推关系:
d’ = d + 2xi + 3
若d > 0,则取P2为下一个点,此时P2的下一个点的判别式为:
d’ = F(xi + 2, yi – 1.5)= (xi + 2)2 + (yi – 1.5)2 – R2
展开后将d带入可得到判别式的递推关系:
d’ = d + 2(xi - yi) + 5
特别的,在第一个象限的第一个点(0, R)时,可以推倒出判别式d的初始值d0:
d0 = F(1, R – 0.5) = 1 – (R – 0.5)2 – R2 = 1.25 - R
根据上面的分析,可以写出中点画圆法的算法。考虑到圆心不在原点的情况,需要对计算出来的坐标进行了平移,下面就是通用的中点画圆法的源代码:
|
26 void MP_Circle(int xc , int yc , int r) 27 { 28 int x, y; 29 double d; 30 31 x = 0; 32 y = r; 33 d = 1.25 - r; 34 CirclePlot(xc , yc , x , y); 35 while(x < y) 36 { 37 if(d < 0) 38 { 39 d = d + 2 * x + 3; 40 } 41 else 42 { 43 d = d + 2 * ( x - y ) + 5; 44 y--; 45 } 46 x++; 47 CirclePlot(xc , yc , x , y); 48 } 49 } |
参数xc和yc是圆心坐标,r是半径,CirclePlot()函数是参照圆的八分对称性完成八个点的位置计算的辅助函数。
2、 改进的中点画圆法-Bresenham算法
中点画圆法中,计算判别式d使用了浮点运算,影响了圆的生成效率。如果能将判别式规约到整数运算,则可以简化计算,提高效率。于是人们针对中点画圆法进行了多种改进,其中一种方式是将d的初始值由1.25 – R改成1 – R,考虑到圆的半径R总是大于2,因此这个修改不会响d的初始值的符号,同时可以避免浮点运算。还有一种方法是将d的计算放大两倍,同时将初始值改成3 – 2R,这样避免了浮点运算,乘二运算也可以用移位快速代替,采用3 – 2R为初始值的改进算法,又称为Bresenham算法:
|
52 void Bresenham_Circle(int xc , int yc , int r) 53 { 54 int x, y, d; 55 56 x = 0; 57 y = r; 58 d = 3 - 2 * r; 59 CirclePlot(xc , yc , x , y); 60 while(x < y) 61 { 62 if(d < 0) 63 { 64 d = d + 4 * x + 6; 65 } 66 else 67 { 68 d = d + 4 * ( x - y ) + 10; 69 y--; 70 } 71 x++; 72 CirclePlot(xc , yc , x , y); 73 } 74 } |
3、 正负判定画圆法
除了中点画圆算法,还有一种画圆算法也是利用当前点产生的圆函数进行符号判别,利用负反馈调整以决定下一个点的产生来直接生成圆弧,就是正负法,下面就介绍一下正负法的算法实现。
正负法根据圆函数:F(x, y)= x2 + y2 – R2的值,将平面区域分成圆内和圆外,如图(3)所示:
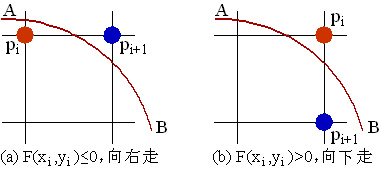
图(3)正负法判定示意图
假设圆弧的生成方向是从A到B方向,当某个点Pi被确定以后,Pi的下一个点Pi+1的取值就根据F(xi, yi)的值进行判定,判定的原则是:
1、当F(xi, yi)≤ 0时:取xi+1 = xi+1,yi+1 = yi。即向右走一步,从圆内走向圆外。对应图(3-a)中的从Pi到Pi+1。
2、当F(xi, yi)> 0时:取xi+1 = xi,yi+1 = yi - 1。即向下走一步,从圆外走向圆内。对应图(3-b)中的从Pi到Pi+1。
由于下一个点的取向到底是向圆内走还是向圆外走取决于F(xi, yi)的正负,因此称为正负法。对于判别式F(xi, yi)的递推公式,也要分两种情况分别推算:
1、当F(xi, yi)≤ 0时,Pi的下一个点Pi+1取xi+1 = xi+1,yi+1 = yi,判别式F(xi+1, yi+1)的推算过程是:
F(xi+1, yi+1)= F(xi+1,yi) = (xi+1)2+yi2-R2 = (xi2+yi2-R2)+2xi+1 = F(xi,yi)+2xi+1
2、当F(xi, yi)> 0时,Pi的下一个点Pi+1取xi+1 = xi,yi+1 = yi - 1,判别式F(xi+1, yi+1)的推算过程是:
F(xi+1, yi+1)= F(xi,yi-1) = xi2+(yi-1)2 - R2 = (xi2+yi2-R2) - 2yi + 1 = F(xi,yi) - 2yi+1
设画圆的初始点是(0,R),判定式的初始值是0,正负法生成圆的算法如下:
|
105 void Pnar_Circle(int xc, int yc, int r) 106 { 107 int x, y, f; 108 109 x = 0; 110 y = r; 111 f = 0; 112 while(x <= y) 113 { 114 CirclePlot(xc, yc, x, y); 115 if(f <= 0) 116 { 117 f = f + 2 * x + 1; 118 x++; 119 } 120 else 121 { 122 f = f - 2 * y + 1; 123 y--; 124 } 125 } 126 } |
改进的中点划线算法和正负法虽然都避免了浮点运算,并且计算判别式时用到的乘法都是乘2运算,可以用移位代替,但是实际效率缺有很大差别。因为正负法并不是严格按照x方向步进的,因此就会出现在某个点的下一个点在两个位置上重复画点的问题,增加了不必要的计算。此外,从生成圆的质量看,中点画圆法和改进的中点画圆法都比正负法效果好。
4、 快速画圆法
除了中点画圆法和正负法,本文再介绍一种圆的光栅扫描算法,就是快速画圆法。快速画圆法的生成效果和中点画圆法差不多,但是判别式的计算只用了加减法,没有用任何乘法,因此被成为快速画圆法。我找不到快速画圆法的理论依据,只是把算法的实现写出来,供有兴趣的读者参考。以下就是快速画圆法的实现算法:
|
128 void Fast_Circle(int xc , int yc , int r) 129 { 130 int x, y, d; 131 132 x = 0; 133 y = r; 134 d = -r / 2; 135 CirclePlot(xc , yc , x , y); 136 if(r % 2 == 0) 137 { 138 while(x < y) 139 { 140 x++; 141 if(d < 0) 142 d += x; 143 else 144 { 145 y--; 146 d += x - y; 147 } 148 149 CirclePlot(xc , yc , x , y); 150 } 151 } 152 else 153 { 154 while(x < y) 155 { 156 x++; 157 if(d < 0) 158 d += x + 1; 159 else 160 { 161 y--; 162 d += x - y + 1; 163 } 164 165 CirclePlot(xc , yc , x , y); 166 } 167 } 168 } |
圆的光栅扫描转换算法有很多种,本文介绍的几个都是简单易懂的算法,除了本文介绍的几种方法外,还有很多种圆光栅转换算法,比如多边形逼近算法等等,有兴趣的读者可以参考计算机图形学方面的资料自己研究算法的实现。
参考资料:
【1】计算几何:算法设计与分析 周培德 清华大学出版社 2005年
【2】计算几何:算法与应用 德贝尔赫(邓俊辉译) 清华大学出版社 2005年
【3】计算机图形学 孙家广、杨常贵 清华大学出版社 1995年