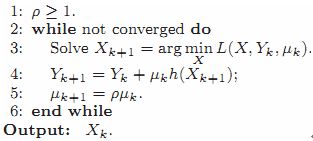Robust PCA

Robust PCA  

1. RPCA 简介

1. 1 为什么使用RPCA?

求解被高幅度尖锐噪声而不是高斯分布噪声污染的信号分离问题。

1.2  主要问题

给定C = A*+B*, 其中A*是稀疏的尖锐噪声矩阵，B* 是低秩矩阵, 目的是从C中恢复B*.

B*= UΣV’, 其中U∈R^n*k ,Σ∈R^k*k ,V∈R^n*k

3. 与PCA的区别

PCA和RPCA 的目的都是矩阵分解, 然而,

对于PCA, M = L0+N0,    L0:低秩矩阵 ; N0: 小的idd Gaussian噪声矩阵, 通过最小化||M-L||_{2  且}满足条件rank(L)<=k来搜索L0的最好秩k估计.通过SVD可以解决这个问题.

对于RPCA, M = L0+S0, L0:低秩矩阵 ; S0: 稀疏尖峰噪声矩阵, 接下来将给出具体的求解过程.

2. 正确分解的条件

4. 病态问题:

假设稀疏矩阵A* 和B*=e_ie_j^T 是分解问题的解.

1) 假设B* 不仅低秩而且稀疏, 可找到另一个稀疏加低秩分解A₁= A*+ e_ie_j^T 和B₁ = 0, 因此, w我们需要对低秩有一个合理的认识确保B* 不是太稀疏. 稍后附加条件需要由奇异向量U和V所张成的空间 (也就是B*的行列空间)与标准基“不连贯” 。

2)  相似地, 假设A* 是稀疏且低秩的 (例如A*的第一列非零, 其他列为0, 则 A* 秩为1且是稀疏的). 可找到另一个有效的分解 A₂=0,B₂ = A*+B* (这里秩(B₂) <= 秩(B*) + 1). 因此我们需要限制稀疏矩阵不应该是低秩的.即, 假设每一行/列不应该有太多的非零元素 (不存在稠密的行/列), 避免这种情况发生.

5.  正确恢复/分解的条件:

如果A* 和B* 来自于这些类时, 则可以高概率获得精确恢复[1].

1)  对于低秩矩阵L---随机正交模型[Candes andRecht 2008]:

以如下方式构建秩k矩阵B* 其SVD分解为B*=UΣV’ : 奇异向量U,V∈R^n*k 来自于对R^{n*k 中}秩k偏等距算子^{的简单随机抽样}. U和V的奇异向量不需要相互独立. 对奇异值无任何约束.

2) 对于稀疏矩阵S---随机稀疏模型:

矩阵A* 使得支撑(A*) 随机等可能地采样于尺度m的所有支撑集合中. There is no assumption made about the values of A* at locations specified by support(A*).

[Support(M)]: M中非零元素的位置

Latest [2] improved on the conditions and yields the ‘best’ condition.

 

3. 恢复算法

6.     Formulization

对于分解D = A+E,其中A是低秩误差E是稀疏的.

1)  凭直觉提出

min rank(A)+γ||E||₀,    (1)

然而这时非凸的，因此难于处理 (两者是NP-hard需要近似处理).

2)  放松条件L0-范数至L1范数，用核范数代替秩

min||A||_* + λ||E||₁,

where||A||_* =Σ_iσ_i(A)   (2)

这是凸的, 也就是存在唯一的最小值解.

理由: 注意到||A||_* + λ||E||_{1    是rank(A)+γ||E||0 在满足条件max(||A||2,2,||E||1, ∞)≤1上的集合(A,E) 的}凸包.

此外, there might be circumstances under which (2) perfectly recovers low-rank matrix A₀.[3] shows it is indeed true under surprising broad conditions.

 

7.   求解RPCA 的优化算法

采用两种不同的方法求解. 第一种方法, 直接使用一阶方法求解邻近问题. (E.g. 邻近梯度, 加速邻近梯度(APG)), 每一次迭代的计算瓶颈是一个SVD计算.第二种方法是将问题转换为对偶问题求解, 从对偶优化解中重新得到邻近解. RPCA的对偶问题为:

max_Ytrace(D^TY) , subject to J(Y) ≤ 1

其中J(Y) = max(||Y||₂,λ^-1||Y||_∞). ||A||_x 指A的x范数.(无穷范数表示矩阵中绝对值最大的一个)。这个对偶问题可通过约束最速上升法求解.

现在讨论增广拉格朗日乘子法 (ALM)和交替方向法(ADM) [2,4].

7.1. ALM的一般方法

对于优化问题

min f(X), subj. h(X)=0     (3)

定义拉格朗日函数:

L(X,Y,μ) = f(X)+<Y, h(x)>+μ/2||h(X)|| _F²       (4)

其中Y是拉格朗日乘子，μ 是正标量.

ALM的一般方法:

广义拉格朗日乘子算法通过重复令(X_k) = arg min L(X_k,Y_k,μ)求解主成分追踪(principle component pursuit)  ，则拉格朗日乘子矩阵Y_k+1=Y_k+μ(h_k(X))

 

7.2  求解RPCA的ALM算法

在RPCA, 定义(5)式为

X = (A,E), f(x) = ||A||_* + λ||E||₁, h(X) = D-A-E

则拉格朗日函数(6)

L(A,E,Y, μ) = ||A||_* + λ||E||₁+ <Y, D-A-E>+μ/2·|| D-A-E || _F ²

优化过程与广义ALM算法相同. 受对偶问题的启示，令Y的初始值为 Y= Y₀* ，因为这可能使得目标函数值<D,Y₀*> 在合理的条件下较大.

定理1.  算法4中,   (A_k*, E_k*)的任何累积点(A*,E*)RPCA问题的最优解，收敛率至少为O(μ_k^-1).[5]

在这个RPCA算法中, 采用了一个迭代策略. 当优化过程缓慢时，利用了两个等式: (7)、(8)

Sε[W] = arg min_X ε||X||₁+ ½||X-W||_F^{2       （7）}

U Sε[W] V^T = arg min_X ε||X||_*+½||X-W||_F^{2        （8）}

在上述算法中为了优化一个参数而固定另一个. 其中Sε[W] 是软阈值算子. 

BTW,S_u(x) is easily implemented by 2 lines:

S_u(X)= max(x-u , 0);

S_u(X)= S_u(X) + min(X+u , 0);

 

 

 

Now we utilize formulation (7,8) into RPCA problem.

For the objective function (6) w.r.t get optimal E, we can rewrite the objective function by deleting unrelated component into:

f(E) = λ||E||₁+ <Y, D-A-E> +μ/2·|| D-A-E|| _F ²

       =λ||E||₁+ <Y, D-A-E> +μ/2·||D-A-E || _F ²+(μ/2)||μ^-1Y||² //add an irrelevant item w.r.t E

       =λ||E||₁+(μ/2)(2(μ^-1Y· (D-A-E))+|| D-A-E || _F ²+||μ^-1Y||²) //try to transform into (7)’s form

       =(λ/μ)||E||1+½||E-(D-A-μ^-1Y)||_F²

Finally we get the form of (7) and in the optimizationstep of E, we have

E = S_λ/μ[D-A-μ^-1Y]

,same as what mentioned in algorithm 4.

Similarly, for matrices X, we can prove A=US_1/μ(D-E-μ^-1Y)V is the optimization process of A.

 

 

8. Experiments 

 Here I've tested on a video data. This data is achieved from a fixed point camera and the scene is same at most time, thus the active variance part can be regarded as error E and the stationary/invariant part serves as low rank matrix A. The following picture shows the result. As the person walks in, error matrix has its value. The 2 subplots below represent low rank matrix and sparse one respectively. 

 

9.     Reference:

1)       E. J. Candes and B. Recht. Exact Matrix Completion Via ConvexOptimization. Submitted for publication, 2008.

2)       E. J. Candes, X. Li, Y. Ma, and J. Wright. Robust PrincipalComponent Analysis Submitted for publication, 2009.

3)       Wright, J., Ganesh, A., Rao, S., Peng, Y., Ma, Y.: Robustprincipal component analysis: Exact recovery of corrupted low-rank matrices viaconvex optimization. In: NIPS 2009.

4)       X. Yuan and J. Yang. Sparse and low-rank matrix decompositionvia alternating direction methods. preprint, 2009.

5)       Z. Lin, M. Chen, L. Wu, and Y. Ma. The augmented Lagrangemultiplier method for exact recovery of a corrupted low-rank matrices.Mathematical Programming, submitted, 2009.

6)       Generalized Power method for Sparse Principal Component Analysis