Stanford机器学习---第七讲. 机器学习系统设计
本栏目(Machine learning)包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM(Support Vector Machines 支持向量机)、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。(https://class.coursera.org/ml/class/index)
第七讲. 机器学习系统设计——Machine learning System Design
===============================
(一)、决定基本策略
(二)、Error分析
☆(三)、对Skewed Classes建立Error Metrics
☆(四)、在Precision 和 Recall (精度和召回率)间权衡
(五)、机器学习数据选定
===============================
(一)、决定基本策略
在本章中,我们用一个实际例子<怎样进行垃圾邮件Spam的分类>来描述机器学习系统设计方法。
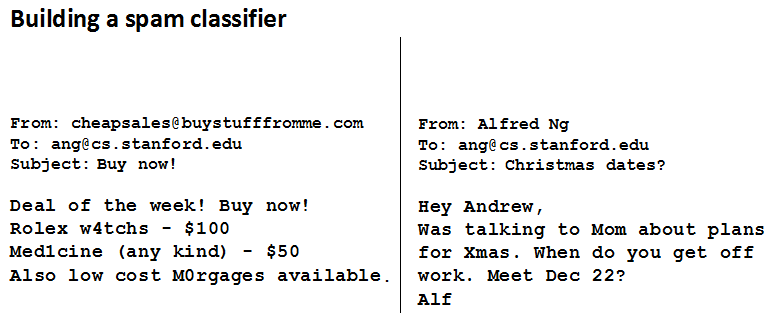
首先我们来看两封邮件,左边是一封垃圾邮件Spam,右边是一封非垃圾邮件Non-Spam:
观察其样式可以发现,垃圾邮件有很多features,那么我们想要建立一个Spam分类器,就要进行有监督学习,将Spam的features提取出来,而希望这些features能够很好的区分Spam vs. Non-Spam.
就如下图所示,我们提取出来deal, buy, discount, now等feature,建立起这样的一个feature向量:
这里请大家注意:事实上,对于spam分类器,我们并非人工选择100个看似是spam feature的feature作为特征,而是选取spam中词频最高的100个词取而代之。
下面就是本节重点——如何决定基本策略,一些可能有利于classifier工作的方法:
- 收集大量数据——如“honeypot" project
- 从Email Route着手建立较为复杂的feature——如发件人为[email protected]
- 对message正文建立复杂精确的feature库——如是否应把discount和discounts视作同一个词等
- 建立算法检查拼写错误,作为feature——如"med1cine"
当然,上述策略并非全部奏效,如下面的练习题所示:
===============================
(二)、Error分析
我们常常在一个ML算法设计的起步阶段有些困惑,要用怎样的系统?建立怎样的模型,feature怎样提取等……
这里呢,我们给大家推荐一个方法,用来建立一个ML系统:
- 用at most 一天,24小时的时间实现一个简单的算法,logistic regression也好,linear regression也好,用simple features而非仔细探究哪个特征更有效。然后呢,在cross-validation数据集上进行测试;
- 利用画learning curves的方法去探究,数据集更多 或者 加入更多features 是否有利于系统工作;
- Error Analysis:上面已经在cross-validation数据集上测试了系统性能,现在呢,我们人工去看是哪些数据造成了大error的产生?是否可以通过改变systematic trend减少error?
还是用Spam-Classifier举例,我们看一下进行Error Analysis的步骤:
- 在建立了simple system 并在CV set上做测试后,我们进行error analysis步骤,将所有spam分为pharma,replica/fake,Steal password 和 其他,这四类。
- 找到一些可能有助于改善分类效果的features。
这里呢,我们不要感性地去想,而是最好用数字体现效果。比如对于discount/discounts/discounted/discounting是否被视为都含有discount这个feature的问题,我们不要主观地去想,而是看如果看都含有这个feature,那么结果是有3%的error,如果不都看做有discount这个feature,则有5%的error,由此可见哪种方法比较好。
PS:介绍一个软件Porter stemmer,可以google到,是将discount/discounts/discounted/discounting视为同类的软件。
对于是否将大小写视作同一个feature是同样的道理。
===============================
(三)、对Skewed Classes建立Error Metrics
有些情况下,Classification-accuracy 和 Classification-error不能描述出整个系统的优劣,比如针对下面的Skewed Classes。
什么是Skewed Classes呢?一个分类问题,如果结果仅有两类y=0和y=1,而且其中一类样本非常多,另一类非常少,我们称这种分类问题中的类为Skewed Classes.
比如下面这个问题:
我们用一个logistic regression作为预测samples是否为cancer患者的模型。该模型在cross-validation set上测试的结果显示,有1%的error,99%的正确诊断率。而事实上呢,只有0.5%的样本为真正的cancer患者。这样一来,我们建立另一个算法去predict:
function y=predictCancer(x)
y=0; %即忽略x中feature的影响
return;
好了,这么一来,该算法将所有sample预测为非癌症患者。那么只存在0.5%的误差,单纯从classification-error来看,比我们之前做的logistic regression要强,可事实上我们清楚这种cheat方法只是trick,不能用作实际使用。因此,我们引入了Error Metrics这个概念。
考虑一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被 预测成正类,即为真正类(True positive),如果实例是负类被预测成正类,称之为假正类(False positive)。相应地,如果实例是负类被预测成负类,称之为真负类(True negative),正类被预测成负类则为假负类(false negative)。
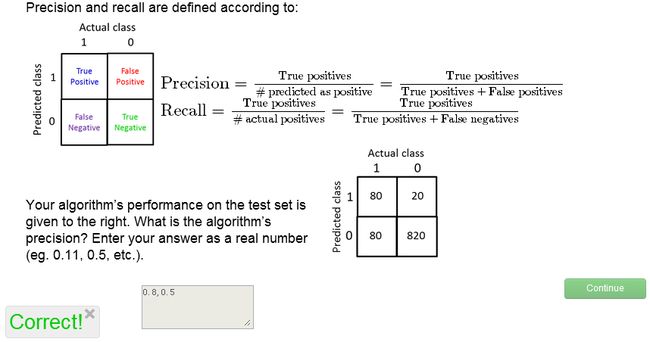
这样就可以建立一个Error Metrics(下图左),并定义precision和recall,如下图所示:
也可参考我原来关于ROC曲线的文章。
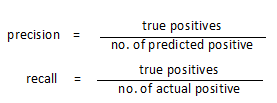
precision:正确预测正样本/我所有预测为正样本的;
recall:正确预测正样本/真实值为正样本的;
当且仅当Precision和Recall都高的时候我们可以确信,该predict算法work well !
ok, 我们再来看看当初将所有sample预测为Non-Cancer的算法,这里,TP=0,FP=0, FN=1, TN=199(假设sample共200个)
由于TP=0, 所以precision=recall=0!证明了该算法的un-avaliable!
所以,无论一个类是否是Skewed Classes,只要满足precision 和 recall都很高才可以保证该算法的实用性。
练习题,做下看:
最后需要提醒大家的是,关于哪边作为true,哪边作为false的问题。对于上面那个问题,我们给定cancer的为true,实际应用中,我们应当在binary classification中指定类中sample较少的那一类作为true,另一类作为false。这一点千万不能搞错!
===============================
(四)、在Precision 和 Recall (精度和召回率)间权衡
对于一个prediction问题,假设我们采用如下方法进行预测:
这里存在一个threshold=0.5。
根据
不同的threshold有如下两类情况:
- 如果我们希望在很确信的情况下才告诉病人有cancer,也就是说不要给病人太多惊吓,我告诉你有cancer,你肯定有cancer;我告诉你没cancer,你也有可能有cancer,那么该情况下有:higher threshold,higher precision,lower recall
- 如果我们不希望让病人错过提前治疗,与上例相反,就有:lower threshold,lower precision,higher recall
这里大家如果想不清楚可以把error metrics画出来看一下。
那么我们可以画出来precision-recall图:
不同的数据,其曲线形式不同,但有一条规律是不变的:
thres高对应高precision低recall;
thres低对应低precision高recall;
☆那么在不同算法或不同threshold造成的的{precision,recall}间,我们怎样选择那个算法比较好呢?
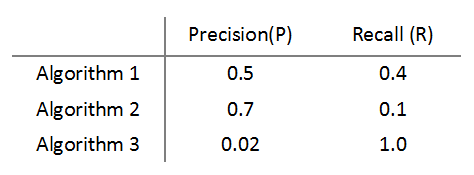
加入我们现在有三个算法(或threshold)的数据:
可见,Algorithm3中,recall=1,即predict所有y=1,这显然违背了我们的初衷。下面看评判标准。用p表示precision,r表示recall;
如果我们选取评判标准=(p+r)/2,则algorithm3胜出,显然不合理。这里我们介绍一个评价标准:F1-Score.
当p=0 或 r=0时,有f=0;
当p=1&&r=1时,有f=1,最大;
同样我们将f1 score 应用于以上三个算法,可的结果,algorithm1最大,也就是最好;algorithm3最小,也就是最差。因此我们用F1 score来衡量一个算法的性能,也就是我们说的precision和recall间的trade-off。
练习,做下吧~(这道略弱):
===============================
(五)、机器学习数据选定
对于机器学习,我们可以选择很多不同的algorithems进行prediction,如:
可见,随着training set的上升,accuracy一般会得到提高,但事实上也不全是这样。
比如房价预测,如果我仅仅给你房子的面积,而没有房子在市中心还是偏远地区?房龄多少?等信息,我们是无法进行良好预测的。
这里就涉及到如何合理处理训练数据及的问题。
记得上一讲中我们已经介绍过了bias和variance的定义和区别,这里我们来看,他们的产生环境:
bias:J(train)大,J(cv)大,J(train)≈J(cv),bias产生于d小,underfit阶段;
variance:J(train)小,J(cv)大,J(train)<<J(cv),variance产生于d大,overfit阶段;
- 想要保证bias小,就要保证有足够多的feature,即linear/logistics regression中有很多parameters,neuron networks中应该有很多hidden layer neurons.
- 想要保证variance小,就要保证不产生overfit,那么就需要很多data set。这里需要J(train)和J(CV)都很小,才能使J(test)相对小。
如下图所示:
综上所述,对数据及进行rational分析的结果是两条:
首先,x中有足够多的feature,以得到low bias;
其次,有足够大的training set,以得到low variance;
练习题:
==============================================
本章重要,讲述了机器学习中如何设计机器学习系统,涉及机器学习方法、策略、算法的问题,希望大家牢牢掌握,以减少不必要的时间浪费。
关于Machine Learning更多的学习资料将继续更新,敬请关注本博客和新浪微博Sophia_qing。