九度OJ题目1516--1557解题练习（十）

题目1516：调整数组顺序使奇数位于偶数前面

题目描述：

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

输入：

每个输入文件包含一组测试案例。
对于每个测试案例，第一行输入一个n，代表该数组中数字的个数。
接下来的一行输入n个整数。代表数组中的n个数。

输出：

对应每个测试案例，
输入一行n个数字，代表调整后的数组。注意，数字和数字之间用一个空格隔开，最后一个数字后面没有空格。

样例输入：

5
1 2 3 4 5

样例输出：

1 3 5 2 4

#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include "math.h"  
 
using namespace std;
 
int main()
{
    int n;
    while (cin >> n)//数的数量
    {
        vector<int> vec(n),odd,even;
        for (int i = 0; i < n; i++)
            cin >> vec[i];
 
        for (int i = 0; i < n; i++)
        {
            if (vec[i] % 2 == 1)
                odd.push_back(vec[i]);
            else
                even.push_back(vec[i]);
        }
        for (size_t i = 0; i < odd.size(); i++)
            cout << odd[i] << " ";
        for (size_t i = 0; i < even.size()-1; i++)
            cout << even[i]<<" ";
        cout << even[even.size() - 1] << endl;
    }
    return 0;
}
/**************************************************************
    Problem: 1516
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:110 ms
    Memory:2560 kb
****************************************************************/

题目1517：链表中倒数第k个结点

题目描述：

输入一个链表，输出该链表中倒数第k个结点。
(hint: 请务必使用链表。)

输入：

输入可能包含多个测试样例，输入以EOF结束。
对于每个测试案例，输入的第一行为两个整数n和k(0<=n<=1000, 0<=k<=1000)：n代表将要输入的链表元素的个数,k代表要查询倒数第几个的元素。
输入的第二行包括n个数t(1<=t<=1000000)：代表链表中的元素。

输出：

对应每个测试案例，
若有结果，输出相应的查找结果。否则，输出NULL。

样例输入：

5 2
1 2 3 4 5
1 0
5

样例输出：

4
NULL

#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>  
 
using namespace std;
//节点定义
class LinkNode
{
public:
    LinkNode(int item)//有参数的构造
    {//函数参数表中的形参允许有默认值，但是带默认值的参数需要放后面  
        next = NULL;
        data = item;
    }
    friend class LinkList;//允许链表类随意访问节点数据
 
private:
    int data;
    LinkNode *next;
};
 
// 带头结点的单链表定义 
class LinkList
{
public:
    LinkList()
    {
        head = new LinkNode(0);//头结点,并未该节点赋值0  
        nLength = 0;
    }
    ~LinkList(){}
    //定位指定的位置，返回该位置上的结点指针  
    LinkNode* Locate(int pos);
    //在指定位置pos插入值为item的结点，失败返回false  
    bool Insert(int item, int pos);
    //打印倒数第k个链表节点
    void Print(int k);
 
private:
    LinkNode *head;//头结点指针
    int nLength;//统计节点长度，不算头结点
};
 
//返回链表中第pos个元素的地址,第0个元素是头结点
LinkNode* LinkList::Locate(int pos)
{
    LinkNode *p = head;
    int i = 0;
    while (p != NULL && i < pos)//p==NULL说明是末尾了
    {
        p = p->next;
        i++;
    }
 
    return p;
}
 
//在pos位置的节点后面插入新节点并赋值item
bool LinkList::Insert(int item, int pos)
{
    LinkNode *p = Locate(pos);
    LinkNode *newNode = new LinkNode(item);//创建新节点，该节点值为item  
    //建立连接，注意新节点是插在pos位置的后面
    newNode->next = p->next;
    p->next = newNode;
    nLength++;
    return true;
}
void LinkList::Print(int k)
{
    LinkNode *p = Locate(this->nLength - k + 1);//第零个节点是头结点，不用输出
    cout << p->data << endl;
}
 
int main()
{
    int n = 0, k = 0, val = 0;
    while (cin>>n>>k)
    {
        if (n > 0)
        {
            LinkList list;
            for (int i = 0; i < n; i++)
            {
                cin >> val;
                list.Insert(val, i);//在第i个位置之后插入值为val的节点
            }
            if (k == 0 || k > n)
            {
                cout << "NULL" << endl;
                continue;
            }
            list.Print(k);
        }
        else
        {
            cout << "NULL" << endl;
            continue;
        }
    }
    return 0;
}
/**************************************************************
    Problem: 1517
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:390 ms
    Memory:3104 kb
****************************************************************/

题目1518：反转链表

题目描述：

输入一个链表，反转链表后，输出链表的所有元素。
(hint : 请务必使用链表)

输入：

输入可能包含多个测试样例，输入以EOF结束。
对于每个测试案例，输入的第一行为一个整数n(0<=n<=1000)：代表将要输入的链表的个数。
输入的第二行包含n个整数t(0<=t<=1000000)：代表链表元素。

输出：

对应每个测试案例，
以此输出链表反转后的元素，如没有元素则输出NULL。

样例输入：

5
1 2 3 4 5
0

样例输出：

5 4 3 2 1
NULL

#include "iostream"
using namespace std;
 
//节点定义
class LinkNode
{
public:
    LinkNode(int item)//有参数的构造
    {//函数参数表中的形参允许有默认值，但是带默认值的参数需要放后面  
        next = NULL;
        data = item;
    }
    friend class LinkList;//允许链表类随意访问节点数据
 
private:
    int data;
    LinkNode *next;
};
 
// 带头结点的单链表定义 
class LinkList
{
public:
    //有参数的构造函数  
    LinkList(int size)
    {
        head = new LinkNode(0);//头结点,并未该节点赋值0  
        nLength = 0;
    }
    ~LinkList(){}
    //定位指定的位置，返回该位置上的结点指针  
    LinkNode* Locate(int pos);
    //在指定位置pos插入值为item的结点，失败返回false  
    bool Insert(int item, int pos);
    //反转链表
    void Reverse(int len);
 
private:
    LinkNode *head;//头结点指针
    int nLength;//统计节点长度，不算头结点
};
 
//返回链表中第pos个元素的地址,第0个元素是头结点
LinkNode* LinkList::Locate(int pos)
{
    LinkNode *p = head;
    int i = 0;
    while (p != NULL && i < pos)//p==NULL说明是末尾了
    {
        p = p->next;
        i++;
    }
 
    return p;
}
 
//在pos位置的节点后面插入新节点并赋值item
bool LinkList::Insert(int item, int pos)
{
    LinkNode *p = Locate(pos);
    LinkNode *newNode = new LinkNode(item);//创建新节点，该节点值为item  
    //建立连接
    newNode->next = p->next;
    p->next = newNode;
    nLength++;
    return true;
}
void LinkList::Reverse(int len)
{
    for (size_t i = 0; i < len; i++)
    {
        LinkNode *p = Locate(len-i);
        if (i==0)
            cout << p->data;
        else
            cout <<" "<< p->data;
    }
    cout << endl;
}
 
int main()
{
    int n = 0, val = 0;
    while (cin>>n)
    {
        if (n == 0)
        {
            cout << "NULL" << endl;
            continue;
        }
        LinkList s(n);
        for (int i = 0; i < n; i++)
        {
            cin >> val;
            s.Insert(val, i);//在第i个位置插入值为val的节点
        }
        s.Reverse(n);
    }
    return 0;
}
/**************************************************************
    Problem: 1518
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:650 ms
    Memory:2972 kb
****************************************************************/

题目1522：包含min函数的栈

题目描述：

定义栈的数据结构，请在该类型中实现一个能够得到栈最小元素的min函数。

输入：

输入可能包含多个测试样例，输入以EOF结束。
对于每个测试案例，输入的第一行为一个整数n(1<=n<=1000000)， n代表将要输入的操作的步骤数。
接下来有n行，每行开始有一个字母Ci。
Ci=’s’时，接下有一个数字k，代表将k压入栈。
Ci=’o’时，弹出栈顶元素。

输出：

对应每个测试案例中的每个操作，
若栈不为空，输出相应的栈中最小元素。否则，输出NULL。

样例输入：

7
s 3
s 4
s 2
s 1
o
o
s 0

样例输出：

3
3
2
1
2
3
0

#include <stdio.h>
#include <iostream>
 
using namespace std;
 
class Stack
{
public:
    Stack(int size)
    {
        elements = new int[size];
        top = -1;
    }
    ~Stack()
    {
        delete[] elements;
        elements = NULL;
    }
    bool push(int ndata);//压入元素到栈顶
    void popTop();//弹出栈顶元素
    void getMin();//获取栈顶元素
private:
    int *elements;
    int top;                     //始终指向栈顶,top=0,就表示有一个数据了  
};
 
//压入元素
bool Stack::push(int ndata)
{
    top++;
    elements[top] = ndata;//从栈顶压入元素 
    return true;
}
 
//获取栈顶元素
void Stack::getMin()
{
    int min = 1000001;
    if (top == -1)//栈空  
    {
        cout << "NULL" << endl;
        return;
    }
    else
    {
        for (int i = 0; i <= top; i++)
        {
            if (min > elements[i])
                min = elements[i];
        }
    }
    cout << min << endl;
}
 
//除去栈顶元素
void Stack::popTop()
{
    if (top > -1)
        top--;
}
 
int main()
{
    int n = 0;
    while (scanf("%d",&n)!=EOF)
    {
        cin.get();//换新行准备让ch接收字符，如果没有将错误，找了好久才发现，他妈的
        Stack s(10000);
        char ch = '0';
        int num = 0;
        for (int i = 0; i < n; i++)
        {
            cin >> ch;
            switch (ch)
            {
            case 's'://压栈栈顶
                cin >> num;
                s.push(num);
                break;
            case 'o'://弹出栈顶
                s.popTop();
                break;
            default:
                break;
            }
            s.getMin();
        }
    }
}
/**************************************************************
    Problem: 1522
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:170 ms
    Memory:1520 kb
****************************************************************/

题目1526：朋友圈

题目描述：

假如已知有n个人和m对好友关系（存于数字r）。如果两个人是直接或间接的好友（好友的好友的好友...），则认为他们属于同一个朋友圈，请写程序求出这n个人里一共有多少个朋友圈。
假如：n = 5 ， m = 3 ， r = {{1 , 2} , {2 , 3} , {4 , 5}}，表示有5个人，1和2是好友，2和3是好友，4和5是好友，则1、2、3属于一个朋友圈，4、5属于另一个朋友圈，结果为2个朋友圈。

输入：

输入包含多个测试用例，每个测试用例的第一行包含两个正整数 n、m，1=<n，m<=100000。接下来有m行，每行分别输入两个人的编号f，t（1=<f，t<=n），表示f和t是好友。 当n为0时，输入结束，该用例不被处理。

输出：

对应每个测试用例，输出在这n个人里一共有多少个朋友圈。

样例输入：

5 3
1 2
2 3
4 5
3 3
1 2
1 3
2 3
0

样例输出：

2
1

#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
 
using namespace std;
 
class UFSet
{
public:
    UFSet(int nsize)
    {
        size = nsize;
        parent = new int[size];
    };
    ~UFSet()
    {
        delete[] parent;
        parent = NULL;
    };
    void makeSet(int n);////初始化每个元素的祖先
    int findSet(int x);//找到元素x的祖先元素
    void unionSet(int a, int b);//若两个元素的祖先不同，则将x元素的祖先设置为y元素的祖先
    int getSets(int n);//获取集合数量
private:
    int *parent;//存放祖先节点，例如x=parent[i]，元素i的祖先节点为元素x
    int size;
};
 
void UFSet::makeSet(int n) //初始化
{
    //初始化每一个元素都各自为一个独立的集合，其祖先均设定为自身
    for (size_t i = 1; i <= n; i++)
        parent[i] = i;
}
 
int UFSet::findSet(int x)
{
    //找到元素所在的集合，也就是找到自己的最高的祖先，
    //这也是判断两个元素是否在同一个集合中的主要依据。
    if (parent[x] == x)
        return x;
     
    parent[x] = findSet(parent[x]);//找到祖先，而不是父节点
    return parent[x];
}
 
void UFSet::unionSet(int x, int y)
{
    //将x和y所在的集合进行合并，利用findSet()判断x和y所在的集合是否相同，
    //如果不同，则要把其中一个元素的祖先指向另一个元素的祖先。
    int ux = findSet(x);//获取节点x的祖先
    int uy = findSet(y);
    if (ux != uy)
        parent[ux] = uy;
}
int UFSet::getSets(int n)
{
    int count = 0;
    for (int i = 1; i <= n; i++)
    {//如果存在某一个节点的祖先是自身说明他是孤立的或者本身就是祖先
        if (parent[i] == i)
            count++;
    }
    return count;
}
 
int main()
{
    int m, n;
    while (cin >> n >> m)
    {
        UFSet uset(100000);
        uset.makeSet(n);//初始化
        //接收m对关系
        int x = 0, y = 0;
        for (int i = 0; i<m; i++)
        {
            cin >> x >> y;
            uset.unionSet(x, y);
        }
        cout << uset.getSets(n) << endl;
         
    }
    return 0;
}
/**************************************************************
    Problem: 1526
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:550 ms
    Memory:1912 kb
****************************************************************/

题目1533：最长上升子序列

题目描述：

给定一个整型数组， 求这个数组的最长严格递增子序列的长度。 譬如序列1 2 2 4 3 的最长严格递增子序列为1，2，4或1，2，3.他们的长度为3。

输入：

输入可能包含多个测试案例。
对于每个测试案例，输入的第一行为一个整数n(1<=n<=100000)：代表将要输入的序列长度
输入的第二行包括n个整数，代表这个数组中的数字。整数均在int范围内。

输出：

对于每个测试案例，输出其最长严格递增子序列长度。

样例输入：

4
4 2 1 3
5
1 1 1 1 1

样例输出：

2
1

1,动态规划法

#include "iostream"    
#include "stdio.h"
#include "vector"  
using namespace std;
int LongNoDrop(const vector<int> &Arr, vector<int> &dp);
int main()
{
    int n = 0;
    while (scanf("%d",&n)!=EOF)
    {
        vector<int> srcArr(n, 0);
        for (size_t i = 0; i < n; i++)
            cin >> srcArr[i];
        vector<int> dp(n, 0);//记录第1个元素到第i个元素之间的不降长度    
        //cout << LongNoDrop(srcArr, dp) << endl;
                 printf("%d", LongNoDrop(srcArr, dp) );
    }
    return 0;
}
//动态规划法：复杂度O（n2），很遗憾，超时
//令dp(i);//记录第1个元素到第i个元素之间的不降长度
int LongNoDrop(const vector<int> &Arr, vector<int> &dp)
{
    int maxLong = 1;
    for (int i = 0; i < Arr.size(); i++)
    {
        dp[i] = 1;//无论计算哪个位置都有1个不降长度  
        for (int j = 0; j < i; j++)
        {//这个遍历的实际意思就是在考虑第i个元素和第j个元素及其以前的元素之间所能形成的不降长度
            if (Arr[i] > Arr[j] && dp[j] >= dp[i])
            {
                dp[i] = dp[j] + 1;//更新该位置的不降长度  
                if (maxLong < dp[i])
                    maxLong = dp[i];//更新最大不降长度  
            }
        }
    }
    return maxLong;
}
/**************************************************************
    Problem: 1533
    User: EbowTang
    Language: C++
    Result: Time Limit Exceed
****************************************************************/

2，二分法

#include <iostream>
#include "vector" 
 
using namespace std;
int maxLongNoDrop(const vector<int> &Arr)
{
    vector<int> stackVec;
    stackVec.push_back(-999999);//初始化第一个数为一个尽可能小的值
    for (size_t i = 0; i < Arr.size(); i++)
    {
        if (Arr[i] > stackVec.back())//stackVec.back()该数组最前面的这个值
        {
            stackVec.push_back(Arr[i]);//将形成一个有序的数组
        }
        else
        {
            int mid = 0, low = 1, high = stackVec.size()-1;
            //二分检索“数组栈”（有序的）中比当前Arr[i]大的第一个数的位置（为low）
            while (low <= high)
            {
                mid = (low + high) / 2;
                if (Arr[i] > stackVec[mid])
                    low = mid + 1;
                else
                    high = mid - 1;
            }
            //替换之
            stackVec[low] = Arr[i];
        }
    }
 
    return (stackVec.size() - 1);
}
 
int main()
{
    int n = 0;
    while (cin>>n)
    {
        vector<int> srcArr(n, 0);
        for (size_t i = 0; i < n; i++)
            cin >> srcArr[i];
        cout << maxLongNoDrop(srcArr) << endl;
    }
    return 0;
}
/**************************************************************
    Problem: 1533
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:380 ms
    Memory:2688 kb
****************************************************************/

题目1537：买卖股票

题目描述：

给定一个大小为n的数组，数组的元素a[i]代表第i天的股票价格。
设计一个算法，计算在最多允许买卖k次（一买一卖记为一次）的条件下的最大收益。
需要注意的是，你不能同时拥有两份股票。也就是说在下次买入前，你必须把手头上原有的股票先卖掉。

输入：

输入可能包含多个测试案例。
对于每个测试案例，输入的第一行为两个整数n和k(1<=n,k<=1000)。
输入的第二行包括n个整数，范围在[0,10000)，代表数组中的元素。

输出：

对应每个测试案例，输出最大获益。

样例输入：

5 1
3 4 5 1 4
7 2
1 2 3 5 6 1 7

样例输出：

3
11

#include "algorithm"
#include <iostream>
#include "stack"
#include <cstring>
#include <cmath>  
 
using namespace std;
 
 
//一般思路：暴力获取后面的值减去前面值的差，取最大的一个
//本题必须禁止出现递减的情况，不然你觉得呢。
//本体和背包问题一样，有两个变量，第i天，交易第j次
//用profit[i][j]表示前i天交易j次能得到的最大利润
//对于第i天的物品有两种选择：交易（买或者卖）或者不做任何交易
//如果不做任何交易：显然，此时的最大利润还是前一天的最大利润profit[i-1][j]
//如果交易：
//为了能在这一天获得最大利润如果执行交易只能卖股票（不能买）：
//那么假设第j次交易的买进股票是在第z天 ，0<z<i,，那么必定有j-1次交易完成在z天以内
//所以这一次交易的利润就是price[i] - price[z]
//那么这种情况下的最大利润profit[i][j] 就是 profit[z][j-1] + price[i]-price[z]
//那么当我们遍历到i，即在每次加上price[i]这个已知值时，先求出profit[z][j-1]-price[z]这个临时利润值maxtmp
//其实就是模拟：用手头已有的利润减去买股票的支出，对于临时利润它必须也是最大的（可以反正法证明）
//每一次可以买，也可以不买
//若不买：显然还是以前的maxtmp，即不变
//若买：为了能最大显然是，用截止到第i天的最大利润减去前一天的买股票的钱，profit[i][j - 1] - price[i]（这样写代码位置要放正确）
//所以临时利润就是两种情况下的较大者
//综上所诉，最大利润显然就是两种情况的较大者
 
const int MAXN = 1010;
//每一天的股票价格
int price[MAXN];
//profit[i][j] 表示前i天交易j次能得到的最大利润
int profit[MAXN][MAXN];
 
 
int main() 
{
    int n, k; 
    //输入天数和交易次数
    while (cin >> n >> k)
    {//接受每天对应的价格
        for (int i = 1; i <= n; i++) 
            cin >> price[i];
        //初始化
        memset(profit, 0, sizeof(profit));
 
        for (int j = 1; j <= k; j++) 
        {
            int maxTmp = profit[0][j - 1] - price[1];
            for (int i = 1; i <= n; i++) 
            {
                //maxTmp保存着已完成的j-1次交易的最大利润减去买股票后的临时利润
                profit[i][j] = max(profit[i - 1][j], maxTmp + price[i]);//前者为不卖，后者为卖出时的最大利润
                //更新下一次的最大maxTmp：用手头的利润减去前一天（因为i增加了）买股票的钱
                maxTmp = max(maxTmp, profit[i][j - 1] - price[i]);//前者不买。后者买
            }
        }
        cout << profit[n][k] << endl;
 
    }
    return 0;
}
/**************************************************************
    Problem: 1537
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:110 ms
    Memory:5508 kb
****************************************************************/

题目1538：GrassLand密码

题目描述：

由于害怕别人偷玩他的新手机，GrassLand总是为其手机加上锁屏密码。但是毫无规律的密码又不方便自己记忆，于是他有了这么一个主意：
首先GrassLand会有一个仅包含小写字母的明文密码，如horse。
然后，他按照九宫格键盘上字母的标注（下图），将字母转化为相应的数字按键。如h出现在按键4上，那么其对应的数字为4。

按照这个规则，GrassLand的明文密码被加密为46773。
现在他需要你为他编写一个程序来完成这个加密过程，生成密码。

输入：

输入包含多组测试数据，每组测试数据一行，包含一个仅包含小写字母的字符串，其长度小于10000。

输出：

对于每组测试用例，输出为一个仅包含数字的字符串，代表加密后的密码。

样例输入：

horse
strawberry

样例输出：

46773
7872923779

#include "string"
#include <cstdio>  
#include <cstdlib> 
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>  
 
using namespace std;
 
int main() 
{
    string s;
    while (cin >> s)
    {
        int len = s.size();
        for (int i = 0; i<len; i++)
        {
            if (s[i] == 'a' || s[i] == 'b' || s[i] == 'c')
                printf("2");
            else if (s[i] == 'd' || s[i] == 'e' || s[i] == 'f')
                printf("3");
            else if (s[i] == 'g' || s[i] == 'h' || s[i] == 'i')
                printf("4");
            else if (s[i] == 'j' || s[i] == 'k' || s[i] == 'l')
                printf("5");
            else if (s[i] == 'm' || s[i] == 'n' || s[i] == 'o')
                printf("6");
            else if (s[i] == 'p' || s[i] == 'q' || s[i] == 'r' || s[i] == 's')
                printf("7");
            else if (s[i] == 't' || s[i] == 'u' || s[i] == 'v')
                printf("8");
            else if (s[i] == 'w' || s[i] == 'x' || s[i] == 'y' || s[i] == 'z')
                printf("9");
        }
        printf("\n");
    }
    return 0;
}
/**************************************************************
    Problem: 1538
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:50 ms
    Memory:1520 kb
****************************************************************/

题目1545：奇怪的连通图

题目描述：

已知一个无向带权图，求最小整数k。使仅使用权值小于等于k的边，节点1可以与节点n连通。

输入：

输入包含多组测试用例，每组测试用例的开头为一个整数n(1 <= n <= 10000)，m(1 <= m <= 100000)，代表该带权图的顶点个数，和边的个数。
接下去m行，描述图上边的信息，包括三个整数,a(1 <= a <= n),b(1 <= b <= n),c(1 <= c <= 1000000),表示连接顶点a和顶点b的无向边，其权值为c。

输出：

输出为一个整数k，若找不到一个整数满足条件，则输出-1。

样例输入：

3 3
1 3 5
1 2 3
2 3 2
3 2
1 2 3
2 3 5
3 1
1 2 3 

样例输出：

3
5
-1

#include <cstdio>  
#include <ctype.h>
#include <cstdlib>  
#include "queue"
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
 
 
using namespace std;
 
class Edge
{
public:
    Edge()
    {
        dst = 0;
    }
    int avex;
    int bvex;
    int dst;
    bool operator <(const Edge &mode) const
    {
        return dst<mode.dst;
    }
};
 
Edge edge[111000];
 
class UFSet
{
public:
    UFSet(int nsize)
    {
        parent = new int[nsize + 1];
    }
    ~UFSet()
    {
        delete[] parent;
        parent = NULL;
    }
 
    // 初始化每个顶点的祖先为自身
    void makeSet(int n);
 
    // 找到元素x的祖先元素   
    int findSet(int x);
 
    void makeMST(int m,int n);
private:
    int *parent;//存放祖先节点，例如x=parent[i]，元素i的祖先节点为元素x  
     
};
 
void UFSet::makeSet(int n) //初始化      
{
    for (size_t i = 1; i <= n; i++)
        parent[i] = i;
}
 
int UFSet::findSet(int x)
{
 
    if (parent[x] == x)
        return x;
 
    parent[x] = findSet(parent[x]);
    return parent[x];
}
 
 
void UFSet::makeMST(int m,int n)
{
    sort(edge + 1, edge + m + 1);//必须先对边排序（根据边的修建费用），这样才能贪心的形成最小花费    
     
    for (int i = 1; i <= m; i++)
    {
        int baseA = findSet(edge[i].avex);
        int baseB = findSet(edge[i].bvex);
        //总是让小的顶点成为祖先
        if (baseA > baseB)
            parent[baseA] = baseB;  
        else
            parent[baseB] = baseA;
 
        if (findSet(n) == findSet(1))
        {
            cout << edge[i].dst << endl;
            return;
        }
    }
    cout << "-1" << endl;
}
int main()
{
    int n = 0, m = 0;
    while (cin >> n >> m)
    {
        UFSet uset(n);
        uset.makeSet(n);//初始化每个城市的祖先为自身  
        for (int i = 1; i <= m; i++)
            scanf("%d%d%d",&edge[i].avex, &edge[i].bvex, &edge[i].dst);
        uset.makeMST(m, n);
    }
    return 0;
}
/**************************************************************
    Problem: 1545
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:620 ms
    Memory:2820 kb
****************************************************************/

题目1547：出入栈

题目描述：

给定一个初始为空的栈，和n个操作组成的操作序列，每个操作只可能是出栈或者入栈。
要求在操作序列的执行过程中不会出现非法的操作，即不会在空栈时执行出栈操作，同时保证当操作序列完成后，栈恰好为一个空栈。
求符合条件的操作序列种类。
例如，4个操作组成的操作序列符合条件的如下：
入栈，出栈，入栈，出栈
入栈，入栈，出栈，出栈
共2种。

输入：

输入包含多组测试用例，每组测试用例仅包含一个整数n(1<=n<=1000)。

输出：

输出仅一个整数，表示符合条件的序列总数，为了防止总数过多超出int的范围，结果对1000000007取模(mod 1000000007)。

样例输入：

2
4
10

样例输出：

1
2
42

#include <iostream>
using namespace std;
//因为是求最大操作数目，所以考虑动态规划，寻求用子问题推导出较大的子问题
//1，n个操作组成的操作序列，那么为满足题目要求必定是出入栈操作各占一半
//2，第一个操作必为入，最后一个必为出，但是中间情况却的不一定，它既可以是出也可以是入 
//3，令dp[i][j](i >= j)表示入栈i次出栈j次的种类数（共i+j个操作数），那么显然dp[i][0]=1
//并且任何时候入必定比出更多（否则出错）
//但是dp[i][j](在i!=j的情况下)必有第i+j个操作是入两种情况,那么dp[i][j]显然就是两者之和
//状态转移方程dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，
//这个转移方程就是根据只考虑最后一个操作得出的结果，比如假设最后增加的一步是入栈，方法数就为dp[i][j - 1]，
//如果最后一步增加的是出栈，数目就是为dp[i - 1][j]，最后加起来就是需要的总数。
int dp[501][501] = {0};
void maxStackTime(int n)//操作数为n时的最大合法序列数
{
    //初始化
    for (int i = 0; i <= n / 2; i++)
        dp[i][0] = 1; //只入不出均只有一种序列数 
 
    for (int i = 1; i <= n / 2; i++)
    {
        for (int j = 1; j <= i; j++)//入栈数一定大于出栈数，否则会非法操作
        {
            if (i == j)
                dp[i][j] = dp[i][j-1] % 1000000007;//（第i+j个操作）即末尾操作必定是出
            else
                dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % 1000000007;//除去第一个和最后一个操作，中间的操作最大数必定是两种情况之和
        }
    }
    cout << dp[n / 2][n / 2] << endl;
}
int main(void)
{
    int n = 0;
    while (cin >> n)
    {
        if (n % 2 == 1 || n <= 0)//n不能为奇数
        {
            cout << "0" << endl;
            continue;
        }
        maxStackTime(n);
    }
    return 0;
}
/**************************************************************
    Problem: 1547
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:50 ms
    Memory:2500 kb
****************************************************************/

题目1548：平面上的点

题目描述：

给定平面上的n个点，任意做一条直线，求至多能有几个点恰好落在直线上。

输入：

包含多组测试数据，每组测试数据由一个整数n(0<=n<=100)开始，代表平面上点的个数。
接下去n行每行给出一个点的坐标(x,y)，x、y的绝对值均小于等于100。

输出：

对于每组测试数据，输出一个整数，表示至多能有几个点恰好落在直线上。

样例输入：

2
0 0
1 1
4
0 0
1 1
2 2 
3 6

样例输出：

2
3

暴力破解：

#include <cstdio>  
#include <cstdlib>  
#include "queue"
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>  
 
using namespace std;
 
int a[101][2];
int main()
{
    int n;
    while (cin >> n)
    {
        //接收输入
        for (int i = 0; i<n; i++)
            cin >> a[i][0] >> a[i][1];
 
        int maxpoints = 0;
        //O(n^3)的时间复杂度
        for (int i = 0; i < n - 1; i++)//点i
        {
            for (int j = i + 1; j < n; j++)//点j
            {
                int tmpcount = 0;
 
                if (a[i][0] == a[j][0] && a[i][1] == a[j][1])//两点相同则跳过（斜率无穷大）
                    continue;
                //查看所有点是否能和这两个点构成的斜率一样
                for (int k = 0; k<n; k++)
                {
                    if ((a[i][0] - a[k][0])*(a[j][1] - a[k][1]) == (a[j][0] - a[k][0])*(a[i][1] - a[k][1]))
                        tmpcount++;
                }
                maxpoints = max(tmpcount, maxpoints);
            }
        }
        if (n>1 && maxpoints>0)
            cout << maxpoints << endl;
        else
            cout << n << endl;
    }
    return 0;
}
/**************************************************************
    Problem: 1548
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:50 ms
    Memory:1520 kb
****************************************************************/

题目1549：货币问题

题目描述：

已知有面值为1元，2元，5元，10元，20元，50元，100元的货币若干（可认为无穷多），需支付价格为x的物品，并需要恰好支付，即没有找零产生。
求，至少需要几张货币才能完成支付。
如，若支付价格为12元的物品，最少需要一张10元和一张2元，即两张货币就可完成支付。

输入：

输入包含多组测试数据，每组仅包含一个整数p（1<=p<=100000000），为需支付的物品价格。

输出：

对于每组输入数据，输出仅一个整数，代表最少需要的货币张数。

样例输入：

10
11
13

样例输出：

1
2
3

#include <iostream>
 
using namespace std;
 
int getAns(int key)
{//贪心策略的返回最优值
    if (key == 0)
        return 0;
    if (key == 8 || key == 9)
        return 3;
    else if (key == 1 || key == 2 || key == 5)
        return 1;
    else
        return 2;
}
 
int main()
{
    int n;
    while (cin >> n)
    {
        int count=0;
        count += n / 100;//计算百位及其以上
        n = n % 100;//保留个位和十位
        count += getAns(n / 10);//计算十位
        count += getAns(n % 10);//计算个位
        cout << count << endl;
    }
    return 0;
}
/**************************************************************
    Problem: 1549
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:50 ms
    Memory:1520 kb
****************************************************************/

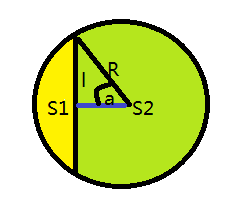
题目1551：切蛋糕

题目描述：

有如下图半价为R的圆形蛋糕，被切一刀后（图中红色直线），分成两个部分（黄色和绿色），已知其比例为r，求刀痕长度（图中红色直线）。

输入：

输入包括多组测试数据，包括一个整数R(1<=R<=1000),和一个浮点数r(0<r<1)，精确到第四位小数。

输出：

对于每组测试用例，输出一个浮点数，代表刀痕的长度，保留二位小数。

分析：

这个题目的主要难度在于分析题目如何解决。

我们得到上图的结果，得S1/S2=r，即S1=r*S2;

又S1+S2=PI*R*R（整个圆的面积）

得到S1=(PI*R*R)*r/(1+r)；

假设刀痕的长度为2L，则其一半为L，且sin(a)=l/R

则a=arcsin(l/R)

扇形面积为S3=R*R*（2*a）/2

三角形的面积为S4=L*sqrt(R*R-L*L)/2

所以S1new=S3-2*S4

由于这个L是未知的我们可以初始化其值，让S1new和S1的差精确到0.00000001（甚至更小）

参考资源：http://blog.csdn.net/yangnanhai93/article/details/41046547

样例输入：

1000 0.5000
500 0.6183

样例输出：

1928.53
982.49

#include <iomanip>//小数点精确
#include <cstdio>  
#include <cstdlib>  
#include "queue"
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
 
using namespace std;
 
const double Pi = 3.1415926;
int main()
{
    int R = 0;
    double r = 0.0;
    while (cin >> R >> r)
    {
        if (r > 1)
            r = 1.0 / r;
        double low = 0.0, high = R*1.0;
        double s1 = Pi*R*R*r / (1 + r);//将s1的面积已知,用来控制精度(s1+s2=Pi*R*R)
        double l=0.0, result=0.0;
        while (true)
        {
            l = (low + high) / 2;//初始化l
            result = R*R*asin(l / R) - sqrt(R*R - l*l)*l;//根据公式求出s1的面积（受到l的影响）
            if (abs(result - s1)<0.0000001)//控制精度
                break;
            if (result>s1)//慢慢缩减到准确值
                high = l;
            if (result<s1)
                low = l;
        }
        cout <<fixed<<setprecision(2)<< 2 * l << endl;
    }
    return 0;
}
/**************************************************************
    Problem: 1551
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:50 ms
    Memory:1600 kb
****************************************************************/

题目1552：座位问题

题目描述：

计算机学院的男生和女生共n个人要坐成一排玩游戏，因为计算机的女生都非常害羞，男生又很主动，所以活动的组织者要求在任何时候，一个女生的左边或者右边至少有一个女生，即每个女生均不会只与男生相邻。现在活动的组织者想知道，共有多少种可选的座位方案。

例如当n为4时，共有
女女女女, 女女女男, 男女女女, 女女男男, 男女女男, 男男女女, 男男男男
7种。

输入：

输入包含多组测试用例，每组测试用例仅包含一个整数n(1<=n<=1000)。

输出：

对于每组测试用例，输出一个数代表可选的方案数，为防止答案过大，答案对1000000007取模。

样例输入：

1
2
4

样例输出：

1
2
7

#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
 
using namespace std;
 
//最值方案问题，考虑采用动态规划
//令dp[i][0]表示共i个人的座位方式，且最后一个是男生，dp[i][1]则是女生
//无论什么时候最后一个人要么是男要么是女
//如果最后一个是男生，显然dp[i][0] = dp[i - 1][0] + dp[i - 1][1];
//因为前面的女生已经满足座位关系，再加一个男生一样满足座位关系
//如果最后一个是女生，显然它的前一个不能是男生，那么只能是女生，
//此时方式数目就是dp[i-1][1]
//但是dp[i-1][1]中并没包括这个女生前面可以是男生的情况（因为我们最后一个是女生，且倒数第二个也是女生，此时才允许这种情况），此时数目是dp[i-2][0]
const int maxx = 1001;
const int MOD = 1000000007;
long  dp[maxx][2];
void init()
{
    long sum = 0;
 
    dp[1][0] = 1;//男生
    dp[1][1] = 0;//女生
 
    dp[2][0] = 1;//男生
    dp[2][1] = 1;//女生
    for (int i = 3; i<1001; ++i)
    {
        //男生
        dp[i][0] = dp[i - 1][0] + dp[i - 1][1];
        dp[i][0] %= MOD;
        //女生
        dp[i][1] = dp[i - 2][0] + dp[i - 1][1];
        dp[i][1] %= MOD;
    }
}
 
int main(){
    long  n, ans;
 
    init();
 
    while (cin>>n)
    {
        ans = (dp[n][0] + dp[n][1]) % MOD;
        cout << ans << endl;
    }
    return 0;
}
/**************************************************************
    Problem: 1552
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:50 ms
    Memory:1536 kb
****************************************************************/

题目1553：时钟

题目描述：

如图，给定任意时刻，求时针和分针的夹角(劣弧所对应的角)。

输入：

输入包含多组测试数据，每组测试数据由一个按hh:mm表示的时刻组成。

输出：

对于每组测试数据，输出一个浮点数，代表时针和分针的夹角（劣弧对应的角），用角度表示，结果保留两位小数。

样例输入：

03:00
14:45

样例输出：

90.00
172.50

#include <iomanip>//小数点精确
#include <cstdio>  
#include <cstdlib>  
#include "queue"
#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
 
using namespace std;
 
 
int main()
{
    int hour = 0, minute = 0;
    char c;
    while (cin >> hour >> c >> minute)
    {
        double nminute = minute * 6.0;//计算分针的角度
        if (hour > 12)
            hour = hour - 12;
        double nhour = hour * 5 * 6.0 + minute / 60.0*30.0;//计算时针的角度
        double angel = nminute - nhour;//角度差
        //分四种情况
        if (angel > 180)
            cout << fixed << setprecision(2) << 360.0 - angel << endl;
        else if (angel < 0 && (angel > -180 || angel == -180))
            cout << fixed << setprecision(2) << - angel << endl;
        else if (angel < -180)
            cout << fixed << setprecision(2) << 360.0 + angel << endl;
        else
            cout << fixed << setprecision(2) <<angel << endl;
    }
    return 0;
}
/**************************************************************
    Problem: 1553
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:50 ms
    Memory:1520 kb
****************************************************************/

题目1555：重复子串

题目描述：

给定一个由小写字母组成的字符串，求它的所有连续子串中，出现过至少两次，且至少有一对出现的重复子串是不重合的连续子串个数。
如给定字符串aaaa，aa和a，符合条件，aaa不符合条件(出现重合)，故答案为2。

输入：

输入包含多组测试用例，每组测试用例包含一个字符串，由小写字母组成，其长度不大于1000。

输出：

对于每组测试数据，输出一个整数，代表符合条件的子串个数。

样例输入：

aaaa
aaa

样例输出：

2
1

#include "vector"
#include "string"
#include "algorithm"
#include <iostream>
#include "stack"
#include <cmath>
#include <set>
 
//参考资源：http://accepted.com.cn/jobduoj1555/
using namespace std;
int main(){
    set<string> get;
    string s;
    while (cin >> s)
    {
        get.clear();
        for (int i = 0; i < s.length(); i++)//从位置i开始寻找子串
        {
            for (int j = 1; i + j + j <= s.length(); j++)//截取长度为j的子串，且j一定小于等于（len-i）/2
            {
                string b = s.substr(i, j);//从字符串s的位置i开始，截取j个字符
                string e = s.substr(i + j, string::npos);//从i+j开始后面全部字符串
                if (e.find(b) != string::npos)//在e中查找是否存在字符串b
                    get.insert(b);
                else
                    break;//同一个i情况下，如果当前的b在e找不到，则更长的b在对应的e中肯定找不到
            }
        }
        cout << get.size() << endl;
    }
    return 0;
}
/**************************************************************
    Problem: 1555
    User: EbowTang
    Language: C++
    Result: Accepted
    Time:160 ms
    Memory:1524 kb
****************************************************************/