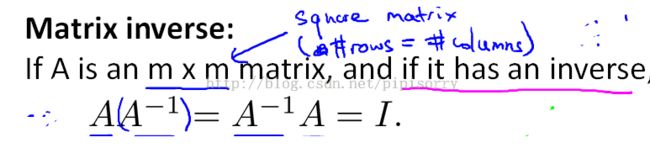Machine Learning - III. Linear Algebra Review线性代数 (Week 1, Optional)
http://blog.csdn.net/pipisorry/article/details/43490965
机器学习Machine Learning - Andrew NG courses学习笔记
Linear Algebra Review线性代数复习
矩阵和向量及其表示介绍
what are matrices矩阵
matrix is just another way for saying, is a 2D or a two dimensional array.
dimension of the matrixis going to be written as the number of row times the number of columns in the matrix.
written out as R4 by 2 or concretely what people will sometimes say this matrix is an element of the set R 4 by 2.
matrix elements,(entries of matrix) the numbers inside the matrix.
the matrix gets you a way of letting you quickly organize, index and access lots of data.
what are vectors向量
A vector turns out to be a special case of a matrix.A vector is a matrix that has only 1 column so you have an N x 1 matrix.{本course中的vector都是列向量}
dimension:if have N equals four elements here.so we also call this is a four dimensional vector, just means that this is a vector with four elements, with four numbers in it.
refer to this as a vector in the set R4.
Notation关于符号的规范表示:
throughout the rest of these videos on linear algebra review, I will be using one index vectors.课程中大多向量下标都是从1开始。
when talking about machine learning applications, sometimes explicitly say when we need to switch to, when we need to use the zero index vectors as well.讨论机器学习应用时会转换到下标从0开始。
Finally, by convention,use upper case to refer to matrices.So we're going to use capital letters like A, B, C.and usually we'll use lowercase,like a, b, x, y,to refer to either numbers,or just raw numbers or scalars or to vectors.
矩阵运算
Matrix Addition and Scalar Multiplication矩阵加法和标量乘法
Scalar Multiplication:multiply a matrix by a number
Matrix Vector Multiplication矩阵向量相乘
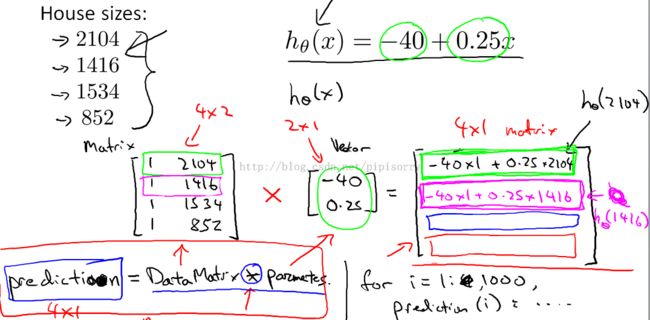
Example applying to the house price prediction
(theta0\1已经计算出来后,左边是用matrix乘法同时预测多个house size对应的房价; 右边是用for循环一个一个地计算)
矩阵计算的优势
code on the left allows you to not only simplify the code,But, for subtle reasons,to be much more computationally efficient to make predictions on all of the prices of all of your houses doing it the way on the left than the way on the right than if you were to write your own formula.
matrix, matrix multiplication
重要性的体现:When we talk about the method in linear regression for how to solve for the parameters,theta zero and theta one, all in one shot.So, without needing an iterative algorithm like gradient descent.

Example:
have four houses whose prices we want to predict,but now we have three competing hypothesis.if you want to apply all 3 competing hypotheses to all four of the houses
(假设有3个不同的模型函数来预测4个house size对应的房价)

matrix multiplying的优势
most popular programming languages will have great linear algebra libraries are highly optimized to do matrix matrix multiplication very efficiently, including taking advantage of any parallel computation that your computer may be capable of, when your computer has multiple calls or lots of multiple processors, within a processor sometimes there's there's parallelism as well called symdiparallelism [sp].
Matrix Multiplication Properties
not commutative 非交换律
Associative 结合律
Identity Matrix单位矩阵
note:上面这个等式中I的维度是不同的,所以有时在matrix下面带上下标。
Matrix Inverse and Transpose
matrix inverse矩阵的逆
note:only square matrices have inverses
the intuition if you want is that you can think of matrices as not have an inverse that is somehow too close to zero in some sense.
singular or degenerate matrix :(奇异或退化矩阵)
matrix that don't have an inverse Sometimes called a singular matrix or degenerate matrix.
zero zero zero matrix is an example of a matrix that is singular, or a matrix that is degenerate.
matrix transpose矩阵的转置
from:http://blog.csdn.net/pipisorry/article/details/43490965