Machine Learning - XII. Support Vector Machines支持向量机(Week 7)

http://blog.csdn.net/pipisorry/article/details/44522881

机器学习Machine Learning - Andrew NG courses学习笔记

Support Vector Machines支持向量机

{学习复杂非线性函数的有力方法}

优化目标Optimization Objective

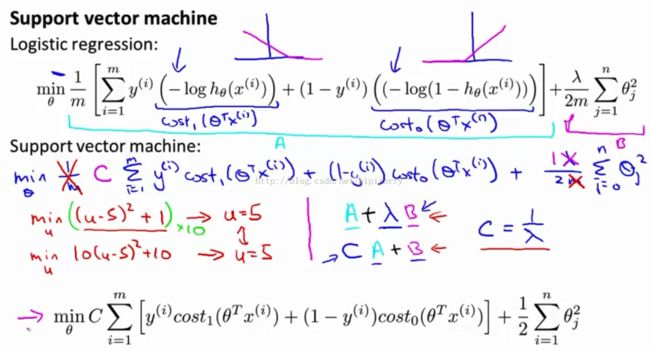
看待逻辑回归的另一种视角

单个样本的cost

Note:

1. 线条表示：蓝色线代表logistic regression， 紫洋红色线代表SVM；

紫洋红色线代表的cost函数给了SVM计算的优势computational advantage， that will give us later on an easier optimization problem, that will be easier for stock trades.

Cost function for SVM

Note:

1. 式中的items A & B：The first term is the cost that comes from the training set A,and the second is the regularization term B(without lambda).
2. 规格化参数lambda对两项的影响：by setting different values for this regularization parameter lambda.We could trade off the relative way between how much we want to fit the training set well,as minimizing A, versus how much we care about keeping the values of the parameters small.
3. SVM中使用新规格化参数C代替lambda:use a different parameter C and we instead are going to minimize C times A plus B.C playing a role similar to 1 over lambda.
So for logistic regression if we send a very large value of lambda, that means to give B a very high weight.Here if we set C to be a very small value corresponds to giving B much larger weight than C than A.

Hypothesis for SVM

Note:

1. SVM doesn't output the probability. I predict 1, if theta transpose x is greater than or equal to 0.And so, having learned the parameters theta, this is the form of the hypothesis for the support vector machine.

intuition: 因为logstic reg的hypothesis是概率，加一个log就可以得到蓝色线条；而SVM中是紫红色线条不能由紫红线条 = log(H)推出H的表达式.

H函数预测错就会有很大的惩罚，y = 1，H预测接近0（不能达到），log(H)就会接近无穷大，H预测接近1（不能达到），log(H)就会接近0

同理SVM中，y = 1，theta transpose x >1时无惩罚，<0时惩罚很大

大边缘的直觉知识Large Margin Intuition

Note:

1. if you have a negative example, then really all you want is that theta transpose x is less than zero and that will make sure we got the example right.But the svm don't just barely get the example right.So then don't just have it just a little bit bigger than zero. What i really want is for this to be quite a lot bigger than zero say maybe bitgreater or equal to one.And so this builds in an extra safety factor or safety margin factor into the support vector machine.

2. theta已经得到后，theta transpose x >= 0 时预测y = 1； 和 在学习theta的值时想要theta transpose x >= 1(这是最小化cost fun的目标) 没有太大关系， 尤其是参数C设置相当大的时候，更要theta transpose x >= 1使得cos1() = 0

当regularization concept C非常大的时候

Note:

1. The svm will instead choose this black decision boundary.
2. The black line seems like a more robust separator, it does a better job of separating the positive and negative examples.
this black decision boundary has a larger distance called the margin,gives the SVM a certain robustness, because it tries to separate the data with as a large a margin as possible.

3. 对C的取值应该在分类是否犯错和margin的大小上做一个平衡。那么C取较大的值会带来什么效果呢？SVM是一个large margin classifier。
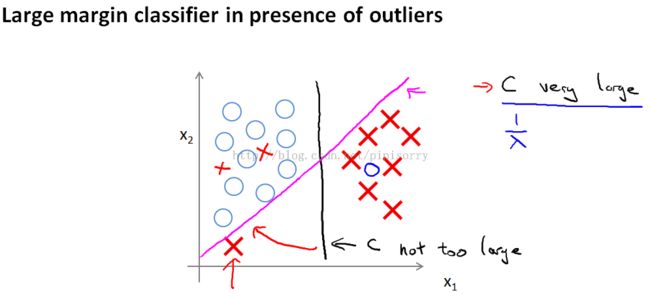
什么是margin？在第三章中decision boundary，它是能够将所有数据点进行很好地分类的h(x)边界。如图所示，我们可以把绿线、粉线、蓝线或者黑线中的任意一条线当做decision boundary，但是哪一条最好呢？绿色、粉色、蓝色这三类boundary离数据非常近，再加进去几个数据点，很有可能这个boundary就能很好的进行分类了，而黑色的decision boundary距离两个类都相对较远，我们希望获得的就是这样的一个decision boundary。margin呢，就是将该boundary进行平移所得到的两条蓝线的距离，如图所指。

对outliers敏感

Note:

1. And in particular, if use a large margin classifier then your learning algorithms can besensitive to outliers
2. add an extra positive example like that shown on the screen.if the regularization parameterC were very large, then SVM will change the decision boundary from the black to the magenta one
3. but if C were reasonably small you still end up with this black decision boundary.
4. in practice when applying support vector machines,when C is not very very large,it can do a better jobignoring the few outliers like here. And also do fine even if your data isnot linearly separable.相当于logstic regression中lambda设置较大，防止过拟合，就消去了outliers的影响。

5. 就是说：离群值存在时,c isn't vety large is better

大边缘分类背后的数学

{解释了为什么SVM是一个large margin classifier}

向量内积

SVM决策边界

Note:

1. s.t.约束条件：来自min(cost fun)的第一项，参数C设置很大时，第一项要为0；由于将C设的很大，cost function只剩下后面的那项。采取简化形式，意在说明问题，设θ0=0，只剩下θ1和θ2 whether we include theta zero here or not is not going to matter for the rest of our derivation.    And theta 0 equals 0 that just means that the decision boundary must pass through the origin (0,0).
2. So all the svm is doing in the optimization objective is it's minimizingthe squared norm of the square length of the parameter vector theta.
3. using our earlier method to compute the inner product theta transpose X(i) is to take my example and project it onto my parameter vector theta.
4. theta垂直于边界线： parameter vector theta is actually at 90 degrees to the decision boundary.如边界线theta transpose x >= 0为theta1*x1 + theta2*x2 >= 0时，theta垂直于theta1*x1 + theta2*x2 = 0这条边界。（平面几何基础）
5. if P1 is pretty small, that means that we need the norm of theta to be pretty large, but what we are doing in the optimization objective is trying to find a setting of parameters where the norm of theta is small
6. by choosing the decision boundary shown on the right instead of on the left, the SVM can make the norm of the parameters theta much smaller. So, if we can make the norm of theta smaller and therefore make the squared norm of theta smaller, which is why theSVM would choose this hypothesis on the right instead.

7. this machine ends up with enlarge margin classifiers because its trying to maximize the norm of these P1 which is the distance from the training examples to the decision boundary.
8. when theta is not equal to 0(that means is that you entertain the decision boundaries that did not cross through the origin) this svm is still trying to find the large margin separator that between the positive and negative examples.
9. 图中左边是随便给出的边界线，右边是svm的large margin边界线，svm要做的其实就是： 在参数C很大时，cost fun第一项要为0（cost fun才会小）就有了s.t.的约束条件pi * theta >= 1，同时cost fun第一项为0就要后面的规格化项theta项要小（这样cost fun才会小），这就要theta小，根据约束条件就要pi大，pi大就导致large margin。这就是SVM为什么是large margin classifier的原因。

[SVM数学分析part1+part2]

Kernels核

{the idea of kernels:define extra features using landmarks and similarity functions to learn more complex nonlinear classifiers}

Note: kernel内核之前都是线性内核，即theta transpose x是线性的

非线性决策边界

Note:

using high order polynomials becomes very computationally expensive because there are a lot of these higher order polynomial terms.

So, is there a different or a better choice of the features that we can use to plug into this sort of hypothesis form？

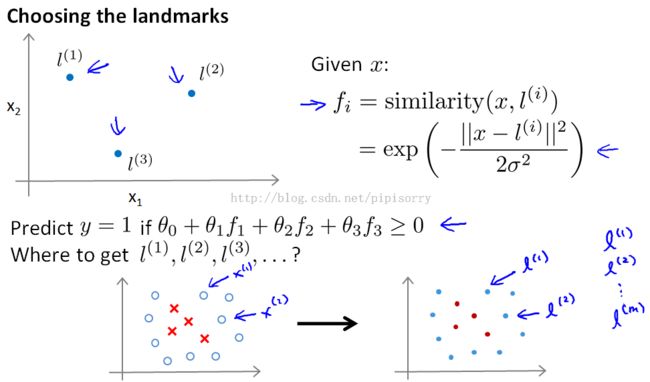
Kernel(similarity fun between x and l)

Note:

1, choose these three points manually for defining new features

2. 红色标注为the euclidean distance squared, is the euclidean distance between the point x and the landmark l1.

3. this particular choice of similarity function is called a Gaussian kernel.高斯分布见[XV. Anomaly Detection异常检测(Week 9) - Gaussian Distribution高斯分布(正态分布)]
what a kernel actually do and why these sorts of similarity functions, why these expressions might make sense?

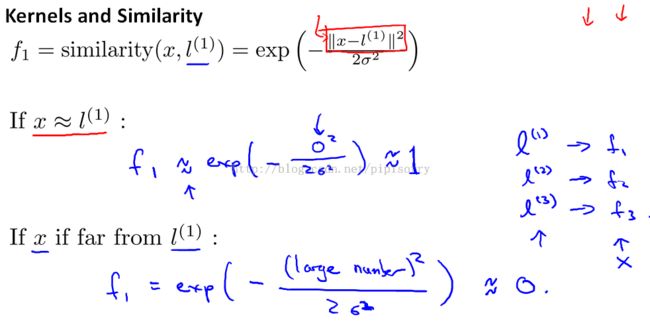
Note:

1. just ignoring the intercept term X0, which is always equal to 1.

2. given the the training example X, we can compute three new features: f1, f2, and f3, given the three landmarks.

3. 从上面可知，算出所有f后，给出某一组theta时可以使边界划分正确，也就是使thetaT* x分类正确，也就是使cost fun最小；所以可以反推，在算出所有f后，求解cost fun最小值就可以得到最优的theta.
look at this similarity function and plot in some figures(sigma对similarity的影响)

Note:

1. feature f1 measures how close X is to the first landmark.这里的l是手动选择的，在后面会讲到怎么选择。

2. if sigma squared is large,value of the feature falls away much more slowly.thewidth of this bell-shaped curve,sigma, is also called one standard deviation.
given this definition of the features,what source of hypothesis we can learn

Note:

1. For this particular example, let's say that I've already found a learning algorithm and somehow I ended up with thesevalues of the parameter.
2. for points near l1 and l2 we end up predicting positive.And for points far away from l1 and l2,we end up predicting that the class is equal to 0.

How do we choose landmarks?

Note:

1. for complex learning problems, maybe we want a lot more landmarks than just three of them that we might choose by hand.
2. put landmarks as exactly the same locations as the training examples.有多少个training example就选择多少个landmarks.the number of landmarks is equal to the training set size.

SVM with Kernels

Note:

1. When you are given example x,and in this example x can be something in the training set,it can be something in the cross validation set, or it can be something in the test set.

2. xi本来是一个n+1 dimesion的vector，转换成f的vector之后就不是n+1,而是m+1了

Hypothsis and how to get parameter theta

Note:

1. because this optimization problem we really have n equals m features.So that n is actually going to be equal to m.

2. we still do not regularize the parameter theta zero

3. what most svm implementations do is actually replace this theta transpose theta,will instead, theta transpose times some matrix inside, that depends on the kernel you use, times theta.That allows the support vector machine software to run much more efficiently.It allows it to scale to much bigger training sets.
4. if you have a training set with 10,000 training examples.Then, you know, the way we define landmarks, we end up with 10,000 landmarks.  it is done primarily for reasons of computational efficiency,
5. because of computational tricks, like that embodied and how it modifies this and the details of how the svm software is implemented, svm and kernels tend go particularly well together.
Whereas, logistic regression and kernels,you know, you can do it, but this would run very slowly.And it won't be able to take advantage of advanced optimization techniques that people have figured out for the particular case of running a support vector machine with a kernel.

the bias variance trade-off in support vector machines(how do you choose the parameters(C & sigma for gaussian kernel) of the svm?)

Note:

1. sigma大小对模型的影响：if sigma squared is large,the Gaussian kernel would tend to fall off relatively slowly and so this would be my feature f(i), and so this would be smoother function that varies more smoothly, and so this will give you a hypothesis with higher bias and lower variance, because the Gaussian kernel that falls off smoothly,you tend to get a hypothesis that varies slowly, or varies smoothly as you change the input x.(x改变时转换后的f(相对原来的x）变化不大，更大范围内fi相近，hypothesis变化不大，更可能预测错误，导致high bias){类似于underfitting}ps:这里可能没特别清楚说明为什么sigma大时会导致high bias。

2. Whereas in contrast,if sigma squared was small and if that's my landmark given my 1 feature x1,my Gaussian kernel, my similarity function, will vary more abruptly(陡峭地).And in both cases I'd pick out 1, and so if sigma squared is small, then my features vary less smoothly.So if it's just higher slopes or higher derivatives here.And using this, you end up fitting hypotheses of lower bias and you can have higher variance.

3. SVM总能找到全局最优值，不会是局部最优。SVM has is a convex optimization problem and so the good SVM optimization software packages willalways find the global minimum or close to it.

Using An SVM 支持向量机的应用

使用SVM软件包求解参数

Note:

1. 使用软件包时还要自己设定参数：1. choice of the parameter's C, about the bias/variance properties. 2. choose the kernel or the similarity function.
2. 使用线性内核的情景：If you have  huge number of features ,with a small training set,maybe you want to just fit a linear decision boundary and not try to fit a very complicated nonlinear function, because might not have enough data.And you might risk overfitting, if you're trying to fit a very complicated function in a very high dimensional feature space, but if your training set sample is small.

Note:

1. SVM software package may ask you to implement a kernel function, or the similarity function.So if you're using an octave or MATLAB implementation of an SVM, it may ask you to provide a function to compute a particular feature of the kernel.
2. feature scaling的原因：If your features take on very different ranges of value.those distances will be almost essentially dominated by the sizes of the houses and the number of bathrooms would be largely ignored.

kernel内核的其它选择

Note :

1. 所有kernel都要满足Mercer定理: because svm algorithms or implementations of the SVM have lots of clever numerical optimization tricks.to solve for the parameter's theta efficiently.
2. The polynomial kernel almost always or usually performs worse.Usually it is used only for data where X and l are all strictly non negative,to ensures these inner products are never negative.And this captures the intuition that X and l are very similar to each other, then maybe the inter product between them will be large.
3. string kernel: sometimes used if your input data is text strings or other types of strings.do text classification problem, where the input x is a string ,to find the similarity between two strings using the string kernel.

多类分类

Note : theta k  is trying to distinguish class y equals k from all of the other classes.

逻辑规划 vs. SVM

Note :

1. If have very very large training set sizes,Gaussian Kernel will be somewhat slow to run.Today's SVM packages,using a Gaussian Kernel, tend to struggle a bit.So try to manually create more features and use logistic regression or an SVM without the Kernel.
2. logistic regression or SVM without a kernel will usually do pretty similar things and give pretty similar performance, but depending on your implementational details, one may be more efficient than the other.But, where one of these algorithms applies,the other one is to likely to work pretty well as well.

[逻辑回归（logistic regression）和支持向量机（SVM）的比较]

Reviews

from:http://blog.csdn.net/pipisorry/article/details/44522881