赫夫曼树之理论概述
转载请注明出处
http://blog.csdn.net/pony_maggie/article/details/41594015
作者:小马
一什么是赫夫曼树
赫夫曼树是指带权路径最短的树,从根结点到叶子结点所经过的结点数(不包括根结点,包括叶子结点)叫路径,如果给叶子结点赋予权值,那么路径和权值的乘积就是访问该叶子结点的代价,对于一棵树来讲,使访问所有的叶子结点的代价最小的树,就是赫夫曼树。
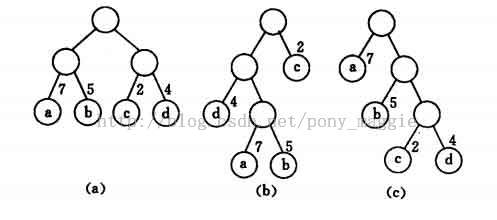
比如下面三个图:
可以计算它们的带权路径长度,分别为
(a) 图是36
(b) 图是46
(c) 图是 35
所以c图是赫夫曼树。
二如何构造赫夫曼树
构造一棵赫夫曼树的步骤其实不复杂,简单来讲就是权值大的尽量靠近根结点,而且是越大的越靠近。这样得出的效果是权值越大的结点,可以经过相对较少的距离到达,从而使程序的效率提高。这里的所说的效率,即包括时间上也包括空间上,后面我会讲到两个应用例子,分别就是一个时间上的优化,一个空间上的优化。
赫夫曼本人给了一个基本的算法,如下:
(1) 将w1、w2、…,wn看成是有n 棵树的集合F(每棵树仅有一个根结点);
(2) 在这些树中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从F中删除选取的两棵树,并将新树加入F
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树
三应用举例
了解的具体的算法之后,必须要知道它的应用场景,不然也就只能停留在理论阶段了。这里给出两个应用的例子。
比如统计一次考试中的学生成绩,划分为5个等级,60分以下为不及格,60到70之间是及格,70到80之间是中等,80到90之间是良好,90到100之间是优秀。本次考试各个阶段学生所占比例如下:
| 分数 | 0-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 比例 | 0.05 | 0.15 | 0.40 | 0.30 | 0.10 |
假设有10000个学生,然后我们用下面的代码来实现统计:
if (a < 60) b = "不及格"; else if (a < 70) b = "及格"; else if (a < 80) b = "中等"; else if (a < 90) b = "良好"; else b = "优秀";
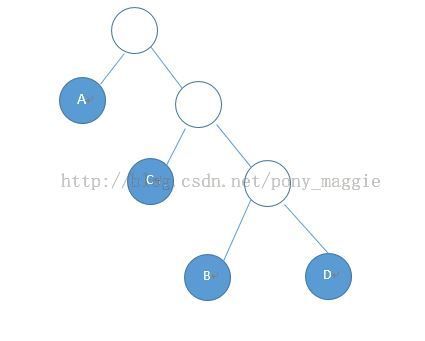
代码对应的树结构如下:
这样一共需要比较30000多次。上面的代码不管你的分数是多少,总要从小于60开始比较,比如一个学生的成绩是85,他要被比较四次才能有结果,不幸的是, 大部分学生的成绩都是在70到90之间,都要经过至少三次以上的比较才能完成。
如果我们能把这个占大多数人的分数区间放在前面,不就可以大大减少比较的次数了吗?先按照前面章节讲的步骤构造一棵赫夫曼树,如下图:
对应的代码是:
if (a >= 70 && a < 80) b = "中等"; else if (a >= 80 && a < 90) b = "良好"; else if (a >= 60 && a < 70) b = "及格"; else if (a < 60) b = "不及格"; else b = "优秀";
这样比较的次数变为22000次,大大提高效率。
再来一个应用的例子。
电报传送时,一般要把字符转成二进制的编码,比如一串字符, “ABACCDA”, 四种字符,可以用二位表示一种,比如A是00, B是01, C是10, D是11,那么电报发送的就是00010010101100,对方收到电报时可以两位一组解出来。
上面的方法没有什么问题,但是一般传送电报肯定希望能用最短的长度传递尽量多的信息,是不是还可以优化呢。当然,我们用不同长度的编码来表示这些字符,出现次数多的字符尽可能的短,出现次数少的可以偏长一些,这样可以构造出一个比上面更短的电报编码。
上面的字符信息,A和C现的次数较多,分别为两次和三次,B和D都是一次。按照上面的方法来构造一棵赫夫曼树,如下:
规则是左0右1, 这样,A是0, B是110, C是10, D是111, 最后的编码是0110010101110, 一共是13个bit位,原来是14个bit位,确实变短了。
再来看看电报接收的一方收到这串编码能不能解出来,试一下发现可以正常解析,不会产生歧义。这是因为任意一个字符的编码都不是另一个字符的编码前缀。这也是二叉树本身自带的一个功能,我们通过这种左0右1的方式得到的编码就可以达到这种效果。
下篇讲如何用代码实现赫夫曼编码