主成分分析(PCA)——以2维图像为例
这一节不论是思想还是实现都比较容易。
主成分分析(PCA)就是模式识别里面说的K-L变换,思想是完全相同的。
详情可见我的博文:特征选择(三)-K-L变换
这里简单介绍几个概念。顺便贴出代码和效果图。
<span style="font-family:Times New Roman;font-size:14px;">xRot = zeros(size(x));
xRot=u'*x;
figure(2);
scatter(xRot(1, :), xRot(2, :));
title('xRot');</span>
得到原始图和主轴方向,如图1所示。
图1
PCA变换
就是要找到数据分布最大的方向,作为主轴方向,然后以这些主轴方向为基,旋转过去,就完成了数据的去相关性,这是因为此时数据的协方差矩阵成了对角阵。如图2所示。
xRot = zeros(size(x));
xRot=u'*x;
figure(2);
scatter(xRot(1, :), xRot(2, :));
title('xRot');
图2
PCA降维
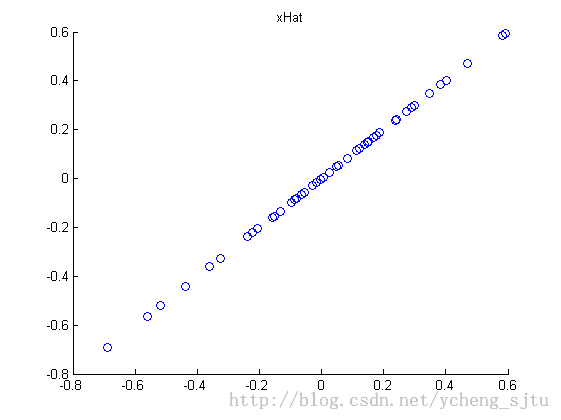
如果我们只取了特征根最大的几个特征向量作为旋转矩阵,那么这就是PCA降维。如图3。
<span style="font-family:Times New Roman;font-size:14px;">k = 1;
xHat = zeros(size(x));
xHat=u(:,1:k)*u(:,1:k)'*x;
figure(3);
scatter(xHat(1, :), xHat(2, :));
title('xHat');</span>
图3
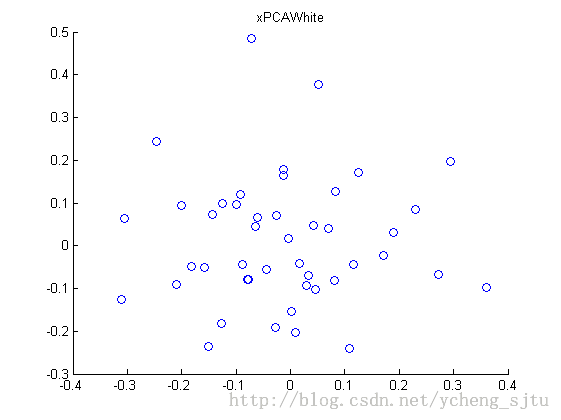
PCA白化
我们不降维,而此基础上将数据左乘一个,那么数据就按照各自主轴方向进行压缩拉伸,成了一个球形,这就是PCA白化。
epsilon = 1e-5;
xPCAWhite = zeros(size(x));
xPCAWhite=diag(1./(diag(s)+epsilon))*u'*x;
figure(4);
scatter(xPCAWhite(1, :), xPCAWhite(2, :));
title('xPCAWhite');
这里加了一个epsilon是因为有的特征根已经很小了,归一化的时候根号了一下,容易出现数据上溢。同时它还有消除噪声的作用。如图4。
图4
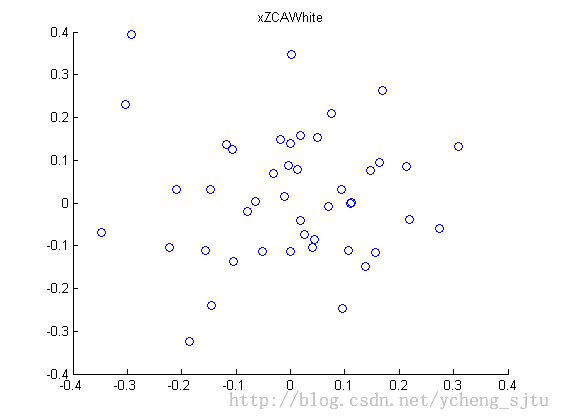
ZCA白化
我们在PCA白化的基础上,左乘一个特征向量矩阵,数据的方向就会又转回去了。这就是ZCA白化,ZCA白化去除了数据的相关性、保留了最大限度原始数据的形式。是数据预处理的好方法。如图5。
xZCAWhite = zeros(size(x));
xZCAWhite=u*diag(1./(diag(s)+epsilon))*u'*x;
figure(5);
scatter(xZCAWhite(1, :), xZCAWhite(2, :));
title('xZCAWhite');
图5
欢迎参与讨论并关注本博客和微博以及知乎个人主页后续内容继续更新哦~
转载请您尊重作者的劳动,完整保留上述文字以及文章链接,谢谢您的支持!