金蝉平方数
参考文献:郭继展,郭勇,苏辉《程序算法与技巧精选》,机械工业出版社,2008年5月第一版,ISBN 978-7-111-23816-4,第5.6节。
定义:设s是一个平方数,由1,2,3,4,5,6,7,8,9,0中无重复的数字组成。s经一次脱壳(即同时去掉其最高位与最低位数字)后剩下的数还是平方数。如果剩下的数仍多于2位,再行脱壳,剩下的数仍是平方数。以此类推,直至最后剩下的数(一位或两位)仍是平方数,这样的数s称为金蝉平方数。
例如:38416是196的平方,38416脱壳后的841是29的平方,841脱壳后的4是2的平方,所以38416是金蝉平方数。
问题:求解出所有的金蝉平方数。
算法分析
(1)s的值必定小于9876543210,否则数字必定重复。
(2)本章思想,平方数问题——算法多从数的平方下手,枚举0~9876543210内的平方数(3万多个),而不是枚举0~9876543210内的每一个数,这是算法优化的关键。
(3)得到平方数后,先判断各个数字的出现有无重复。(用isudig函数实现)
(4)再用一个递归函数判断当前或多次脱壳后是否为平方数。(用isjcpfs函数实现,jcpfs即"金蝉平方数"拼音首字母组合)
实现代码
“mymath.h”:http://blog.csdn.net/code4101/article/details/17993747
“debug.h”:http://blog.csdn.net/code4101/article/details/17993293
#include <iostream>
#include "mymath.h"
#include "debug.h"
using namespace std;
int isjcpfs(__int64 v)
{
if(fmod(sqrt(v),1)) return 0; // 当且仅当fmod(sqrt(v),1)值为0时,v为平方数
else if(v<100) return 1;
v/=10; // 脱去最低位
v%=(int)(pow(10, (int)log10(v))); // 脱去最高位
return isjcpfs(v);
}
int main()
{
int c=0;
__int64 i;
tic;
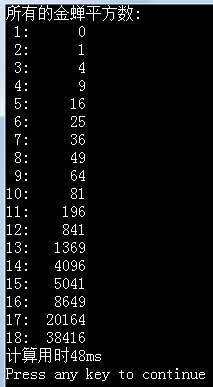
cout << "所有的金蝉平方数:\n";
for(i=0; i<sqrt(9876543210); i++) if(isudig(i*i)) if(isjcpfs(i*i))
printf("%2d: %6I64d\n",++c,i*i);
cout<<"计算用时"; toc;
return 0;
}
运行结果截图