Lua 八皇后问题
1.什么是八皇后问题?
八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后。不知道你们玩过国际象棋没有。皇后在国际象棋中是非常重要的棋子,因为她的移动范围很广,比车,和象都要广,可以横竖走,斜着也可以走,一般死掉皇后,基本就输了。因为每一行都有8种可能,所以一共可能解是8*8*8*8*8*8*8*8所以要想人工在棋盘上摆出八个皇后的所有解,还是蛮难的一件事情。
2.用Lua来解这个问题solution
用什么语言解不是重点,主要我最近在看《Programming in lua》这书,书中给出了答案,感觉写的比较好。第一眼看起来还蛮难的,又是递归!
local N = 8
-- 判断从第1行开始直到当前给定的行,列是否有冲突的皇后
-- 比如一个解{3, 7, 2, 1, 8, 6, 5, 4}, 在判断第4行,第一列是否合法是, isPlaceOK(a, 4, 1)
-- 我们就发现它是与第三行的2有"斜着"冲突
local function isPlaceOK(a,row,column)
for i = 1, row - 1 do
if(a[i] == column) or --相同列
(a[i] - i == column - row) or --斜着冲突, 方向是\
(a[i] + i == column + row) then --斜着冲突, 方向是/
return false
end
end
return true
end
-- 打印一个解
-- 我们这里的解是放在一个table中,类似{3, 7, 2, 1, 8, 6, 5, 4}
local function printSolution(a)
for i = 1, N do
for j = 1, N do
io.write(a[i] == j and "X" or "-", " ")
end
io.write("\n")
end
io.write("\n")
end
--核心方法,独立解释
local function addQueen(a, row)
if row > N then
printSolution(a)
else
for column = 1, N do
if isPlaceOK(a, row, column) then
a[row] = column
addQueen(a, row + 1)
end
end
end
end
addQueen({}, 1)--从第一行开始求解
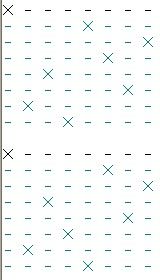
3.程序输出
4.解释下addQueen这个函数
首先这个程序的解的样式是这样的:{3, 7, 2, 1, 8, 6, 5, 4},表示第1行的第3列摆了一个皇后,第2行的第7列摆了一个皇后,后面的以此类推。
首先我们要知道总的可能解是8个8相乘,所以我们要搞一个递归函数来判断8*8*8*8*8*8*8*8个可能解中是否有符合要求的解。 递归主要要处理要退出条件和参数的问题,参数一般不是递增就是递减。我们这里选择从第一行开始放皇后求解,那么参数就是行,每次递增,退出条件就是第9行。每一行,我们要判断8个列中是否能找到合法解,如果能找到合法解,继续往下一行搜索,直到到达函数的退出条件就算是找到一个解了。总的可能解脑补下就是8*8*8*8*8*8*8*8,符合我们的期望。
http://www.waitingfy.com/archives/978