有道难题,决赛第一轮之“如何为实习生安排座位”
ü 问题描述:
N排,每排M个座位,任何两个实习生座位不能水平、垂直或对角线相邻。
输入:string intern[]
intern[]的各元素拼起来得到一串以单个空格隔开的数字。总共N个数字,表示第i排坐了几个实习生。
输出:满足条件的座次安排方案数。因总数可能过大,返回 方案总数%1000000007的结果。
约束:
1. M∈[1,15]
2. intern[]元素个数∈[1,50]
3. intern[]元素长度∈[1,50]
4. intern[]的各元素拼接起来后,得到一串以单个空格隔开的数字,数字不会以0开始,也不会以空格开始或结束,也不会有连续的空格。此串中,有数字个数∈[1,200],每个数字大小∈[0,M]
ü 算法描述:
一看就知道这是个动态规划问题,如果您没看出来,没辙,您就继续看吧~~
但凡DP就要找DP方程!本题方程还算好想:每一排的所有方案,要与上一排的所有方案血拼,拼赢了就和谐了,统计当前和谐指数。就这么反复呀反复,直到最后一排都排好了,全局也就和谐了,输出全局和谐指数就OK!
这里两处“所有”,以及“和谐指数”是关键。傻算一定超啦!该怎么办,先自己想,再往下看~~
1. 给定M,我们可以得到这样一张表:遍历每一排可能的实习生数i(i<M∈[1,15])得到所有可行的方案,当然也就知道了方案数。那么怎么求呢?怎么才能体现不相邻呢?但凡这种时候,二进制总是显地很NB!1表示该位置上有人,0表示没人,穷举所有的可能,只要mask & (mask<<1) == 0就没有水平相邻的情况,无需解释。M<=15,所以一个方案对应一个int. (一会儿看完了回头想想,这是不超时的关键,不打表会WA死人的)
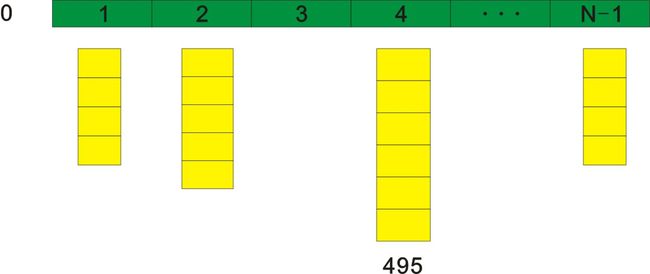
为了估算最坏情况,我们令M=15,打表时发现N=4时的方案数最多495种。最坏不过如此矣!
2. 从输入intern[]得到rows数组,如下所示。Rows[i]表示第i行要坐多少个实习生。
3. 准备工作做完了。动态转移方程到底嘛样儿!别急别急~~
我们用F [ rowNum ] [ ind ]表示“已经安排好0 - rowNum-1行,且第rowNum排现在采用的是可行的第ind个方案(别忘了,从1里我们已经知道了可行的所有的方案)的方案数”。这里ind<=495,F[0][]=1。
到底怎么递推呢?现在就揭开DP方程的神秘面纱!
If 可行,那么F [ rowNum ] [ j ] = ( F [ rowNum ] [ j ] + F [ rowNum-1 ] [ k ] ) %1000000007
什么意思呢?拿本排的第j种方案去跟上一层的每一种方案进行比较for(k),然后再for(j)就是说拿本排的每一种方案上去血拼~~拼赢了,你的财产(方案数)就是我的了!怎么才算赢呢,就是说我的方案要跟你的方案和谐,水平、垂直、对角线都不挨着(换句话说,这位intern gg/mm威力比较大,方圆四周8格均不许有人)。这又怎么表示呢?笨笨~用x和y分别表示本排方案和前排方案:
(x&y) ==0 && (x& (y<<1) ) ==0 & ((x<<1)&y) ==0
符合这个条件,二者就和谐了!
4. 最后要输出的是可行方案数,总不能打一张F[][]表出来吧,罚时罚出心脏病来~~
resolutions = (resolutions + F [ 最后一排] [ i ]) %1000000007
ü 我说两句:
1. 位运算的王者风范,很好很强大。
2. 所有可行的方案打表存储。用一次算一次,您真不懂实惠~~
3. 时间复杂度。最坏是495*495*200 = 49005000,拿你的CPU主频估算一下,会不会TLE~~不会再往上刷~~
4. 我还能不能再优化?
空间:借鉴“背包九讲”P01,显然F[][]可以不用两维,浪费的都是空间~
反正F[i+1][]只与F[i][]有关,正着或反着,一个一维或两个一维,您留意控制一下就行了!
时间:状态数*决策数*决策费用,该削哪一部分呢。。
从方程下手,不太好想~~我再学习一下DD牛的背包九讲再来搬门弄斧。。。
还好此题给定每排的实习生数,如果这个不给定,每排有变,那么复杂度前边得再多一个M^N。。。有兴趣的盆友,可以一起讨论下咯~