论文笔记:Chaotic Invariants of Lagrangian Particle Trajectories for Anomaly Detection in Crowded Scenes
【原创】Liu_LongPo 转载请注明出处
【CSDN】http://blog.csdn.net/llp1992
最近在关注 crowd scene方面的东西,因为某些原因需要在crowd scene上实现 anomaly detection,所以看到了这篇论文,该论文是目前在crowd scene中进行abnormal detection做的最好的,记录下笔记当做学习资料。
传统的 anomaly detection中,很多突发事件监测都是基于motion information的,这样就忽略了由于appreance导致但是又没有造成 motion abnormal的情况下的漏监测。 比如卡车超重在桥上行走
传统的光流法,像素变化直方图,或者是背景差分法都很难应用于 crowd scenes ,因为此时的背景是 dynamic的。
也有将 motion 和 appreance 结合在一起进行abnormal detection的
在crowd scene中,很多一般的abnormal even detection方法都不能取得很好的效果,因为crowd scene的背景是经常剧烈变化的,传统的方法不能充分检测到这种变化。
关于Anomaly detection的,关注得不多,目前看到的方法有以下几种:
- Social force model
- Optical flow
social force model 主流的Optical flow方法有点不同,它主要是考虑crowd scene中的Froce,因此就没有Optical flow中的遮挡问题
该论文提出的方法也是基于 Optical flow的,能够适用于 coherent and incoherent scene,创新点如下:
- 利用粒子轨迹对crowd scene进行建模,并提出具有代表性的trajectories 来对复杂的crowd flows进行建模
- 在 crowd context 中引入 chaotic dynamics(混沌动力学),并通过调节一系列的 chaotic invariant feature来抽取 复杂的crowd motions 信息,这可以用来进行 anomaly detection
- 提出一个概率框架来进行anomaly detection and localization
Significance of Crowd Scene Analysis
- 管理大量人群在有限空间的聚集事件
- 突发事件检测、定位以及警告
- 集群监督,公共场所监控,安全控制等等
如下图,是不同密集层度的集群
challenge
- 检测的人群目标密度非常大
- 有多种运动目标的密集层度,如上图
- 传统方法
- 是适合在稀疏空间
- 会受到严重遮挡,检测目标小,目标appreance类似的问题
另外,在crowd scene中,很多一般的abnormal even detection方法都不能取得很好的效果,因为crowd scene的背景是经常剧烈变化的,传统的方法不能充分检测到这种变化
论文的Idea
拉格朗日质点动力学 + 混沌不变量
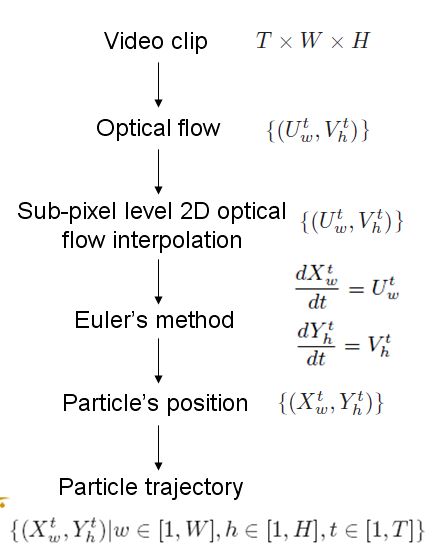
- 框架如下:
论文创新点
- 目前唯一利用粒子轨迹聚类来对crowsed scene 进行建模
- 在 crowd context中引入混沌不变量
- 能够处理连贯和不连贯的人流
Particle Advection
其中, T 是视频帧, W 是视频帧的宽度, H 是视频帧的高度
Cluster Particle Trajectories
- 原则:几条轨迹流可能只是有一个单一的运动目标产生
- 方法:聚类
- step1 : 去除那些相对运动量比较少的点或轨迹,因为它们包含的运动信息比较少
- step2 : 根据轨迹流的位置信息进行K-means聚类
- 输出:聚类后的代表性轨迹流
在step1中去除点或轨迹的标准是轨迹流的方差,设定阈值 ϵ , 去除那些方差比 ϵ 小的轨迹流
轨迹流聚类后如下:
这些聚类后的轨迹流就是 representative trajectories。实验结果证明,突发事件检测基本上对cluster number不敏感
Chaotic Invariants
- Representation of scenes: Representative trajectories
- To identify the scene’s dynamics in terms of the dynamics of representative trajectories: lChaotic dynamics by measurable chaotic invariants
论文中说到,运用上面提取的 representative trajectories 可以创建一个基于 Chaotic Invariants 的模型,该模型能够 handle both coherent and incoherent scenes and offer a description using only two features
也就是两个Chaotic Invariants:largest Lyapunov exponent :L 和 correlation dimension:D。
此外,为了进行 anomaly detection,还增加了feature M,代表的是轨迹流 x 和 y 的平均坐标 M
对于 Chaotic Invariants,我个人不是很懂,理解得不太好。如果有懂得人还望不吝赐教。
Feature Set
由上面可知,本模型得到的特征集如下: F={L,D,M}
- L: Largest Lyapunov exponent
- D: Correlation dimension
- M: Mean of representative trajectories (Only necessary for position-caused anomalies)
则求解 L 和 D 的过程如下:
求解过程还是挺好懂的,就是先找一条轨迹流的最邻近的轨迹流组成轨迹流pairs,然后进行求解 L 和 D
Advantages of the Algorithm
- Proven to be insensitive to the changes in time delay, embedding dimension, size of data set and to some extent noise
- Ensure L>0 for condition of chaotic analysis
计算chaotic feature 时需要的特征比较多,因此本文在轨迹中插入一些点来达到每个事件序列都有500个点
Anomaly Detection
Definition of anomaly: Spatiotemporal change of scene/system dynamics (chaotic or/and positions)
- Global anomaly: entire change of dynamics
- Local anomaly: dynamics changes near particular spatial points
- Approach: Probabilistic model
具体方法如下:
首先运用GMM算法描述正常场景的概率密度函数:
其中:
Γ denotes a four (or six if M features are included) dimensional set of random variables with two features for each time series in x and y
K : 高斯元的个数
u : 均值
Σ : 方差
Φ : 模型参数
Model Learning
Normality model: Multi-variate GMM
- Learning by: EM + IPRA algorithm
- Principle for judging a query as normal or abnormal: Probability of the query belonging to the normality model + ML criterion
也就是,当我们用一些正常的视频序列 S 来训练模型 P(Γ|Φ)=∑Kk=1wkN(Γ;uk,Σk) ,模型的输入每一个 representative trajectories,学习得到模型参数 Φm 后,就可以将测试视频流输入模型,对所有的representative trajectories输出的概率求平均值,根据最大似然准则(ML)将平均值与阈值 Lthres 比较判断测试视频是属于normal还是abnormal。
Anomaly Localization
1.计算每个representative trajectory 对于模型的输出概率
2.定位那些比阈值 Lthres 小的representative trajectory
3.根据位置信息对它们进行聚类得到多个cluster
4.去除那些包含少量trajectories的cluster
5.剩下的那些cluster就是主要的abnormal region
Experiment Results
举个栗子,下面两个图中,人工标记黄色框汇总有人站起来跳舞,其他人在鼓掌,跳舞的人就属于 abnormal 的。(其实只给一帧的图片我看不太出)
这是实验结果,中间的图是检测到的所有的abnormal region,右边是去除那些包含少量trajectories 的cluster后的情况,基本可以定位成功
关于 GMM和EM算法的资料:
http://blog.csdn.net/u012176591/article/details/46051431
K-means聚类和EM思想
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006910.html
(EM算法)The EM Algorithm :
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
高斯混合模型(GMM) :
http://www.cnblogs.com/mindpuzzle/archive/2013/04/24/3036447.html
EM及高斯混合模型:
http://www.cnblogs.com/zhangchaoyang/articles/2624882.html