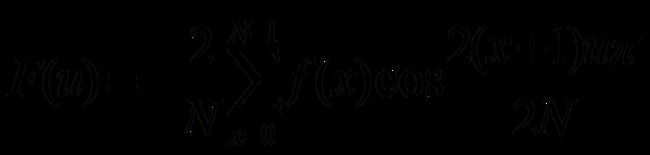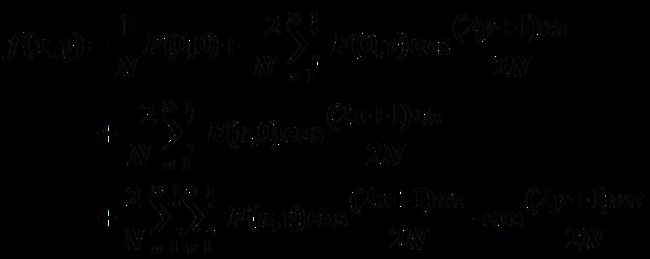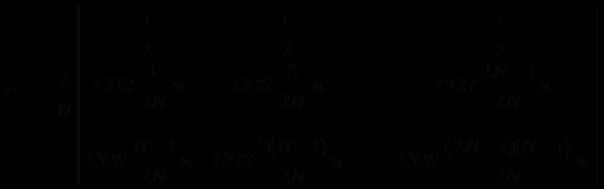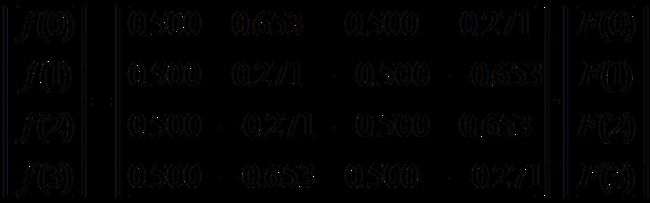离散余弦变换(C++实现)

理论部分转载自这篇blog: http://blog.csdn.net/luoweifu/article/details/8214959  该blog给出的是java代码，我用c++将其实现了。

理论：

图像处理中常用的正交变换除了傅里叶变换外，还有其他一些有用的正交变换,其中离散余弦就是一种。离散余弦变换表示为DCT( Discrete Cosine Transformation)，常用于图像处理和图像识别等。

一维离散余弦变换

正变换

                                   (1)

                            (2)

式中F(u)是第u个余弦变换系数，u是广义频率变量,u=1,2,3......N-1; f(x)是时域N点序列, x=0,1,2......N-1

反变换

  （3）

显然，式(1)式(2)和式(3)构成了一维离散余弦变换对。

二维离散余弦变换

正变换

  （4）

式(4)是正变换公式。其中f(x,y)是空间域二维向量之元素， x,y=0,1,2,......N-1；F(u,v)是变换系数阵列之元素。式中表示的阵列为N×N

反变换

 （5）

式中的符号意义同正变换式一样。式(4)和式(5)是离散余弦变换的解析式定义。

矩阵表示法

更为简洁的定义方法是采用矩阵式定义。根据以上公式定义可知，离散余弦变换的系数矩阵可以写成如下：

如果令N＝4，那么由一维解析式定义可得如下展开式。

写成矩阵式

若定义F(u)为变换矩阵，A为变换系数矩阵，f(x)为时域数据矩阵，则一维离散余弦变换的矩阵定义式可写成如下形式

[F(u)]=[A][f(x)]                       （6）

同理，可得到反变换展开式

写成矩阵式即

[f(x)]=[A]^T[F(u)]                      （7）

二维离散余弦变换也可以写成矩阵式：

[F(u,v)]=[A][f(x,y)][A]^T            （8）

[f(x,y)]=[A]^T[F(u,v)][A]                     

式中[f(x,y)]是空间数据阵列，A是变换系数阵列，[F(u,v)]是变换矩阵，[A]T是[A]的转置。

对二维图像进行离散余弦变换

由以上对二维离散余弦变换的定义及公式（7）可知，求二维图像的离散余弦变换要进行以下步骤：

1.获得图像的二维数据矩阵f(x,y)；

2.求离散余弦变换的系数矩阵[A]；

3.求系数矩阵对应的转置矩阵[A]T；

4.根据公式（7）[F(u,v)]=[A][f(x,y)][A]T 计算离散余弦变换；

以下是我的c++代码实现<当然其中针对的是图像，故用到了opencv的库函数>：

C++代码：

/*
	功能：获取DCT系数
	n：矩阵大小
	quotient: 系数
	quotientT: 系数转置
*/
void coefficient(const int &n, double **quotient, double **quotientT){
	double sqr = 1.0/sqrt(n+0.0);
	for(int i = 0; i < n; i++){
		quotient[0][i] = sqr;
		quotientT[i][0] =  sqr;
	}

	for(int i = 1; i < n; i++){
		for(int j = 0; j < n; j++){
			quotient[i][j] = sqrt(2.0/n)*cos(i*(j+0.5)*PI/n);  // 由公式得到
			quotientT[j][i] = quotient[i][j];
		}
	}

}
/*
	功能：两矩阵相乘
	A和B：源输入矩阵
	result：输出矩阵
*/
void matrixMultiply(double **A, double **B, int n, double **result){  
	double t = 0;
	for(int i = 0; i < n; i++){
		for(int j = 0; j < n; j++){
			t = 0;
			for(int k = 0; k < n; k++)
				t += A[i][k]*B[k][j];   
			result[i][j] = t;
		}
	}
}

//  DCT变换
void DCT(Mat_<uchar> image, const int &n, double **iMatrix){
	for(int i = 0; i < n; i++){
		for(int j = 0; j < n; j++){
			iMatrix[i][j] = (double)image(i,j);
		}
	}

	// 为系数分配空间
	double **quotient = new double*[n];
	double **quotientT = new double*[n];
	double **tmp = new double*[n];
	for(int i = 0; i < n; i++){
		quotient[i] = new double[n];
		quotientT[i] = new double[n]; 
		tmp[i] = new double[n];
	}
	// 计算系数矩阵
	coefficient(n, quotient, quotientT);
	matrixMultiply(quotient, iMatrix, n, tmp);  // 由公式成绩结果
	matrixMultiply(tmp, quotientT, n, iMatrix);

	for(int i = 0; i < n; i++){
		delete []tmp[i];
		delete []quotient[i];
		delete []quotientT[i];
	}
	delete []tmp;
	delete []quotient;
	delete []quotientT;
}