numpy教程 - 数学函数

http://blog.csdn.net/pipisorry/article/details/39235767

numpy数学函数

NumPy提供常见的如sin,cos和exp

更多函数all, alltrue, any, apply along axis, argmax, argmin, argsort, average, bincount, ceil, clip, conj, conjugate, corrcoef, cov, cross, cumprod, cumsum, diff, dot, floor, inner, inv, lexsort, max, maximum, mean, median, min, minimum, nonzero, outer, prod, re, round, sometrue, sort, std, sum, trace, transpose, var, vdot, vectorize

numpy运算

四则运算

add()返回一个数组，它的每个元素都是两个参数数组的对应元素之和。如果没有指定out参数，那么它将创建一个新的数组保存计算结果。如果指定了第三个参数out，则不产生新的数组，而直接将结果保存进指定的数组。

NumPy为数组定义了各种数学运算操作符，因此计算两个数组相加可以简单地写为a+b，而np.add(a,b,a)则可以用a+=b表示。下面列出了数组的运算符和其对应的ufunc函数，注意除号”/”的意义根据是否激活__future__.division有所不同。

y = x1 + x2	add(x1, x2 [, y])
y = x1 - x2	subtract(x1, x2 [, y])
y = x1 * x2	multiply (x1, x2 [, y])
y = x1 / x2	divide (x1, x2 [, y]), 如果两个数组的元素为整数，那么用整数除法
y = x1 / x2	true_divide (x1, x2 [, y]), 总是返回精确的商
y = x1 // x2	floor_divide (x1, x2 [, y]), 总是对返回值取整
y = -x	negative(x [,y])
y = x1**x2	power(x1, x2 [, y])
y = x1 % x2	remainder(x1, x2 [, y]), 或mod(x1, x2, [, y])

数组对象支持操作符，极大地简化了算式的编写，不过要注意如果算式很复杂，并且要运算的数组很大，将会因为产生大量的中间结果从而降低程序的运算效率。例如：假设对a、b、c三个数组采用算式“x=a*b+c”计算，那么它相当于：

t = a * b
x = t + c
del t

也就是说需要产生一个临时数组t保存乘法的运算结果，然后再产生最后的结果数组x。我们可以将算式分解为下面的两行语句，以减少一次内存分配：

x = a*b
x += c

比较和布尔运算

使用“==”、“>”等比较运算符对两个数组进行比较，将返回一个布尔数组，它的每个元素值都是两个数组对应元素的比较结果。例如：

>>> np.array([1,2,3]) < np.array([3,2,1])
array([ True, False, False], dtype=bool)

每个比较运算符也与一个ufunc函数对应，下面是比较运算符和其ufunc函数的对照表：

y = x1 == x2	equal(x1, x2 [, y])
y = x1 != x2	not_equal(x1, x2 [, y])
y = x1 < x2	less(x1, x2, [, y])
y = x1 <= x2	less_equal(x1, x2, [, y])
y = x1 > x2	greater(x1, x2, [, y])
y = x1 >= x2	greater_equal(x1, x2, [, y])

由于Python中的布尔运算使用and、or和not等关键字，它们无法被重载，因此数组的布尔运算只能通过相应的ufunc函数进行。这些函数名都以“logical_”开头，在IPython中使用自动补全可以很容易地找到它们：

>>> np.logical # 按Tab进行自动补全
np.logical_and np.logical_not np.logical_or  np.logical_xor

下面是一个使用logical_or()进行或运算的例子：

>>> a = np.arange(5)
>>> b = np.arange(4,-1,-1)
>>> a == b
array([False, False,  True, False, False], dtype=bool)
>>> a > b
array([False, False, False,  True,  True], dtype=bool)
>>> np.logical_or(a==b, a>b) # 和 a>=b 相同
array([False, False,  True,  True,  True], dtype=bool)

对两个布尔数组使用and、or和not等进行布尔运算，将抛出ValueError异常。因为布尔数组中有True也有False，NumPy无法确定用户的运算目的：

>>> a==b and a>b
ValueError: The truth value of an array with more than one
element is ambiguous. Use a.any() or a.all()

错误信息告诉我们可以使用数组的any()或all()方法[1]。只要数组中有一个值为True，则any()返回True；而只有数组的全部元素都为True，all()才返回True。

>>> np.any(a==b)
True
>>> np.any(a==b) and np.any(a>b)
True

以“bitwise_”开头的函数是比特运算函数，包括bitwise_and、bitwise_not、bitwise_or和bitwise_xor等。也可以使用”&”、”~”、”|”和”^”等操作符进行计算。

对于布尔数组来说，比特运算和布尔运算的结果相同。但在使用时要注意，比特运算符的优先级比比较运算符高，因此需要使用括号提高比较运算的运算优先级。例如：

>>> (a==b) | (a>b)
array([False, False,  True,  True,  True], dtype=bool)

整数数组的比特运算和C语言的比特运算相同，在使用时要注意元素类型的符号，例如下面的arange()所创建的数组的元素类型为32位符号整数，因此对正数按位取反将得到负数。以整数0为例，按位取反的结果是0xFFFFFFFF，在32位符号整数中，这个值表示-1。

>>> ~np.arange(5)
array([-1, -2, -3, -4, -5])

而如果对8位无符号整数数组进行比特取反运算：

>>> ~np.arange(5, dtype=np.uint8)
array([255, 254, 253, 252, 251], dtype=uint8)

同样的整数0，按位取反的结果是0xFF，当它是8位无符号整数时，它的值是255。

Note:在NumPy中同时也定义了any()和all()函数。

自定义ufunc函数

通过NumPy提供的标准ufunc函数，可以组合出复杂的表达式在C语言级别对数组的每个元素进行计算。但有时这种表达式不易编写，而对每个元素进行计算的程序却很容易用Python实现，这时可以用frompyfunc()将一个计算单个元素的函数转换成ufunc函数。这样就可以方便地用所产生的ufunc函数对数组进行计算了。

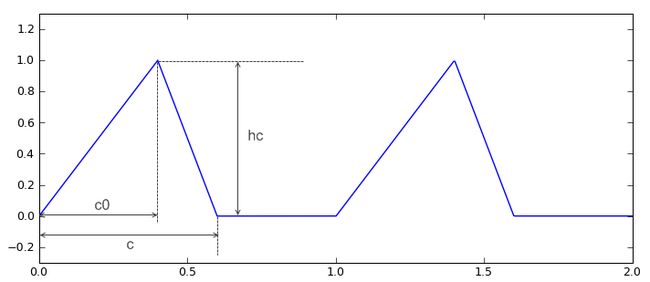
例如，我们可以用一个分段函数描述三角波，三角波的样子如【图:三角波可以用分段函数进行计算】所示，它分为三段：上升、下降和平坦段。

三角波可以用分段函数进行计算

02-numpy/numpy_frompyfunc.py

用frompyfunc()计算三角波的波形数组

根据【图:三角波可以用分段函数进行计算】，我们很容易写出计算三角波上某点的Y坐标的函数。显然triangle_wave()只能计算单个数值，不能对数组直接进行处理。

def triangle_wave(x, c, c0, hc):
    x = x - int(x) # 三角波的周期为1，因此只取x坐标的小数部分进行计算
    if x >= c: r = 0.0
    elif x < c0: r = x / c0 * hc
    else: r = (c-x) / (c-c0) * hc
    return r

我们可以用下面的程序先使用列表推导式计算出一个列表，然后用array()将列表转换为数组。这种做法每次都需要使用列表推导式语法调用函数，对于多维数组是很麻烦的。

x = np.linspace(0, 2, 1000)
y1 = np.array([triangle_wave(t, 0.6, 0.4, 1.0) for t in x])

通过frompyfunc()可以将计算单个值的函数转换为一个能对数组的每个元素进行计算的ufunc函数。frompyfunc()的调用格式为：

frompyfunc(func, nin, nout)

其中func是计算单个元素的函数，nin是func的输入参数的个数，nout是func的返回值个数。下面的程序使用frompyfunc()将triangle_wave()转换为一个ufunc函数对象triangle_ufunc1：

triangle_ufunc1 = np.frompyfunc(triangle_wave, 4, 1)
y2 = triangle_ufunc1(x, 0.6, 0.4, 1.0)

值得注意的是，triangle_ufunc1()所返回的数组的元素类型是object，因此还需要再调用数组的astype()方法将其转换为双精度浮点数组：

>>> run numpy_frompyfunc.py # 在IPython中运行计算三角波的程序
>>> y2.dtype
dtype('object')
>>> y2 = y2.astype(np.float)
>>> y2.dtype
dtype('float64')

使用vectorize()也可以实现和frompyfunc()类似的功能，但它可以通过otypes参数指定返回数组的元素类型。otypes参数可以是一个表示元素类型的字符串，或者是一个类型列表，使用列表可以描述多个返回数组的元素类型。下面的程序使用vectorize()计算三角波：

triangle_ufunc2 = np.vectorize(triangle_wave, otypes=[np.float])
y3 = triangle_ufunc2(x, 0.6, 0.4, 1.0)

最后我们验证一下结果：

>>> np.all(y1==y2)
True
>>> np.all(y2==y3)
True

[ufunc运算]

numpy中数学函数汇总

Trigonometric functions

sin(x[, out])	Trigonometric sine, element-wise.
cos(x[, out])	Cosine element-wise.
tan(x[, out])	Compute tangent element-wise.
arcsin(x[, out])	Inverse sine, element-wise.
arccos(x[, out])	Trigonometric inverse cosine, element-wise.
arctan(x[, out])	Trigonometric inverse tangent, element-wise.
hypot(x1, x2[, out])	Given the “legs” of a right triangle, return its hypotenuse.
arctan2(x1, x2[, out])	Element-wise arc tangent of x1/x2 choosing the quadrant correctly.
degrees(x[, out])	Convert angles from radians to degrees.
radians(x[, out])	Convert angles from degrees to radians.
unwrap(p[, discont, axis])	Unwrap by changing deltas between values to 2*pi complement.
deg2rad(x[, out])	Convert angles from degrees to radians.
rad2deg(x[, out])	Convert angles from radians to degrees.

Hyperbolic functions

sinh(x[, out])	Hyperbolic sine, element-wise.
cosh(x[, out])	Hyperbolic cosine, element-wise.
tanh(x[, out])	Compute hyperbolic tangent element-wise.
arcsinh(x[, out])	Inverse hyperbolic sine element-wise.
arccosh(x[, out])	Inverse hyperbolic cosine, element-wise.
arctanh(x[, out])	Inverse hyperbolic tangent element-wise.

Rounding

around(a[, decimals, out])	Evenly round to the given number of decimals.
round_(a[, decimals, out])	Round an array to the given number of decimals.
rint(x[, out])	Round elements of the array to the nearest integer.
fix(x[, y])	Round to nearest integer towards zero.
floor(x[, out])	Return the floor of the input, element-wise.
ceil(x[, out])	Return the ceiling of the input, element-wise.
trunc(x[, out])	Return the truncated value of the input, element-wise.

Sums, products, differences

prod(a[, axis, dtype, out, keepdims])	Return the product of array elements over a given axis.
sum(a[, axis, dtype, out, keepdims])	Sum of array elements over a given axis.
nansum(a[, axis, dtype, out, keepdims])	Return the sum of array elements over a given axis treating Not a Numbers (NaNs) as zero.
cumprod(a[, axis, dtype, out])	Return the cumulative product of elements along a given axis.
cumsum(a[, axis, dtype, out])	Return the cumulative sum of the elements along a given axis.
diff(a[, n, axis])	Calculate the n-th order discrete difference along given axis.
ediff1d(ary[, to_end, to_begin])	The differences between consecutive elements of an array.
gradient(f, *varargs, **kwargs)	Return the gradient of an N-dimensional array.
cross(a, b[, axisa, axisb, axisc, axis])	Return the cross product of two (arrays of) vectors.
trapz(y[, x, dx, axis])	Integrate along the given axis using the composite trapezoidal rule.

Exponents and logarithms

exp(x[, out])	Calculate the exponential of all elements in the input array.
expm1(x[, out])	Calculate exp(x) - 1 for all elements in the array.
exp2(x[, out])	Calculate 2**p for all p in the input array.
log(x[, out])	Natural logarithm, element-wise.
log10(x[, out])	Return the base 10 logarithm of the input array, element-wise.
log2(x[, out])	Base-2 logarithm of x.
log1p(x[, out])	Return the natural logarithm of one plus the input array, element-wise.
logaddexp(x1, x2[, out])	Logarithm of the sum of exponentiations of the inputs.
logaddexp2(x1, x2[, out])	Logarithm of the sum of exponentiations of the inputs in base-2.

Other special functions

i0(x)	Modified Bessel function of the first kind, order 0.
sinc(x)	Return the sinc function.

Floating point routines

signbit(x[, out])	Returns element-wise True where signbit is set (less than zero).
copysign(x1, x2[, out])	Change the sign of x1 to that of x2, element-wise.
frexp(x[, out1, out2])	Decompose the elements of x into mantissa and twos exponent.
ldexp(x1, x2[, out])	Returns x1 * 2**x2, element-wise.

Arithmetic operations

add(x1, x2[, out])	Add arguments element-wise.
reciprocal(x[, out])	Return the reciprocal of the argument, element-wise.
negative(x[, out])	Numerical negative, element-wise.
multiply(x1, x2[, out])	Multiply arguments element-wise.
divide(x1, x2[, out])	Divide arguments element-wise.
power(x1, x2[, out])	First array elements raised to powers from second array, element-wise.
subtract(x1, x2[, out])	Subtract arguments, element-wise.
true_divide(x1, x2[, out])	Returns a true division of the inputs, element-wise.
floor_divide(x1, x2[, out])	Return the largest integer smaller or equal to the division of the inputs.
fmod(x1, x2[, out])	Return the element-wise remainder of division.
mod(x1, x2[, out])	Return element-wise remainder of division.
modf(x[, out1, out2])	Return the fractional and integral parts of an array, element-wise.
remainder(x1, x2[, out])	Return element-wise remainder of division.

Handling complex numbers

angle(z[, deg])	Return the angle of the complex argument.
real(val)	Return the real part of the elements of the array.
imag(val)	Return the imaginary part of the elements of the array.
conj(x[, out])	Return the complex conjugate, element-wise.

Miscellaneous

convolve(a, v[, mode])	Returns the discrete, linear convolution of two one-dimensional sequences.
clip(a, a_min, a_max[, out])	Clip (limit) the values in an array.
sqrt(x[, out])	Return the positive square-root of an array, element-wise.
square(x[, out])	Return the element-wise square of the input.
absolute(x[, out])	Calculate the absolute value element-wise.
fabs(x[, out])	Compute the absolute values element-wise.
sign(x[, out])	Returns an element-wise indication of the sign of a number.
maximum(x1, x2[, out])	Element-wise maximum of array elements.
minimum(x1, x2[, out])	Element-wise minimum of array elements.
fmax(x1, x2[, out])	Element-wise maximum of array elements.
fmin(x1, x2[, out])	Element-wise minimum of array elements.
nan_to_num(x)	Replace nan with zero and inf with finite numbers.
real_if_close(a[, tol])	If complex input returns a real array if complex parts are close to zero.
interp(x, xp, fp[, left, right])	One-dimensional linear interpolation.

[ Mathematical functions]

Note:

1. np.sin比math.sin快10倍多。这得利于np.sin在C语言级别的循环计算。np.sin同样也支持计算单个数值的正弦值。不过值得注意的是，对单个数值的计算math.sin则比np.sin快很多。在Python级别进行循环时，np.sin的计算速度只有math.sin的1/6。这是因为np.sin为了同时支持数组和单个数值的计算，其C语言的内部实现要比math.sin复杂很多。此外，对于单个数值的计算，np.sin的返回值类型和math.sin的不同，math.sin返回的是Python的标准float类型，而np.sin则返回一个float64类型

from:http://blog.csdn.net/pipisorry/article/details/39235767