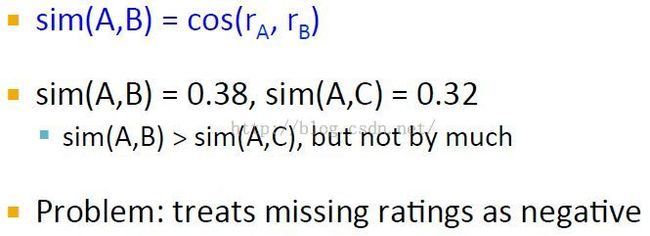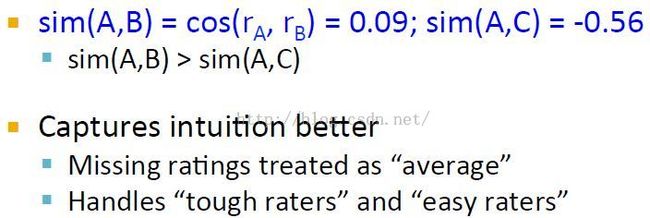海量数据挖掘MMDS week4: 推荐系统Recommendation System

http://blog.csdn.net/pipisorry/article/details/49205589

海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec courses学习笔记 推荐系统Recommendation System

{博客内容：推荐系统构建三大方法：基于内容的推荐content-based，协同过滤collaborative filtering，隐语义模型(LFM, latent factor model)推荐。这篇博客只讲前两种推荐方式及推荐系统的评估方法}

推荐系统综述

综述overview

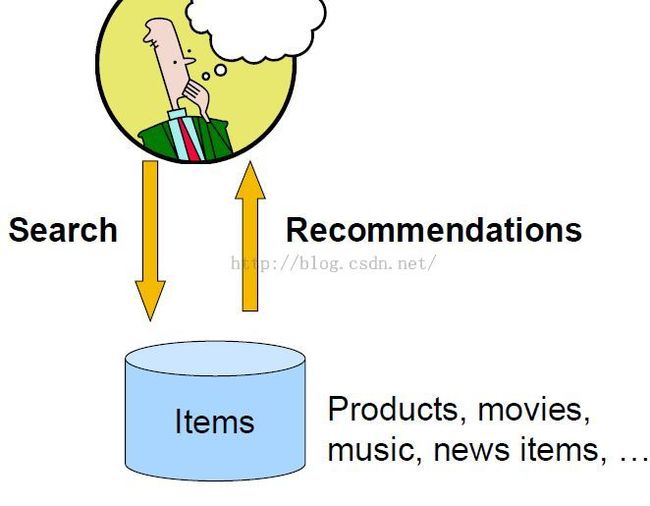
人与物(large catalog of items)的交互的两大方式

搜索和推荐

需要推荐系统的原因

moved from an area scarcity to an area of abundance

货架上的items很少，而网上商店的items是相当丰富的

但是随之而来的是长尾效应

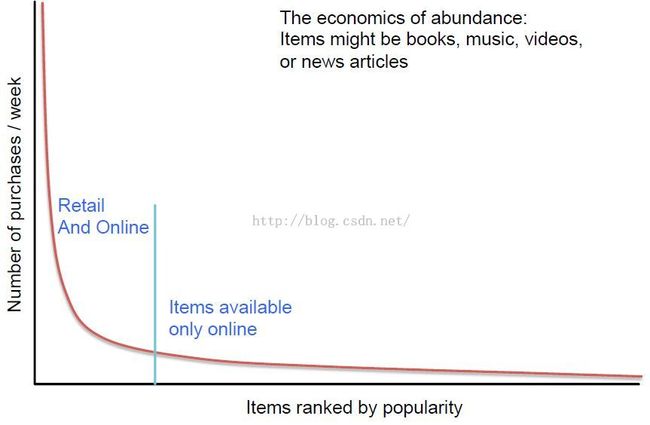
长尾效应Long Tail phenomenon

cutoff point左侧是流行的商品，右侧是不流行的，也称作长尾。长尾下面的面积一般比左侧还大，有太多的items没有被用户发现，这就需要推荐系统帮助人们寻找他们想要的items（注意这里的items也可能是facebook上的人物哦）。

[关于长尾效应的一个营销故事 The Long Tail : How Into Thin Air made Touching the Void a bestseller]

推荐系统的发展

形式化模型Formal Models

                                                                                                                                 Utility Matrix的一个示例：用户*电影->评分

    

Note: function called the utility function or a utility matrix.The utility function looks at every pair of customer and item, and maps it to a rating.

推荐系统要做的其实就是预测Utility Matrix中这些空白的地方的评分值会是多少，再去做相关推荐。

推荐系统三大关键问题

known数据收集；unknown数据推断；评估

收集Ratings

两种方式

现在一般都是两种方式的结合，使用隐性Ratings来补充显式Ratings。

推断评分Extrapolating Utilities

推荐系统两大关键问题

Unitily矩阵庞大而稀疏，冷启动问题

推荐系统存在的问题及构建的三大方法

基于内容的推荐，协同过滤，隐语义模型

皮皮blog

基于内容的推荐Content-based System

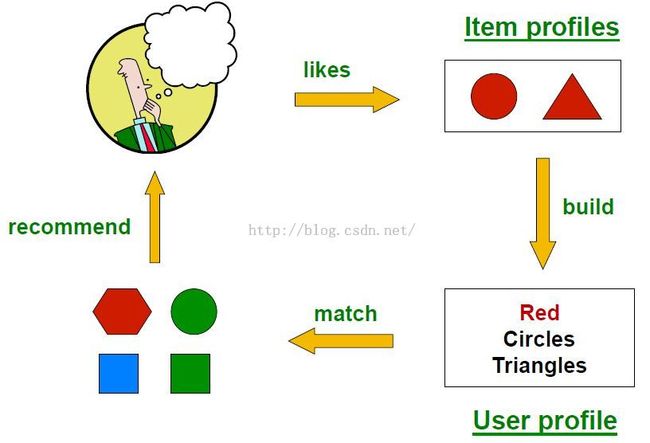
主要思想

Note: 上图同时使用了explict和impliict信息建立Item profiles，推荐时当然是推荐红色的六边形。

Item描述Item Profile

文章推荐中的item描述示例：Text Features

Profile = set of “important” words in item (document)

词重要性度量一般使用文本挖掘的启发式方法：TF-IDF

TF-IDF(Term frequency * Inverse Doc Frequency))

词频（term frequency，TF）指的是某一个给定的词语在该文件中出现的频率。

这个数字是对词数(term count)的归一化，以防止它偏向长的文件。（同一个词语在长文件里可能会比短文件有更高的词数，而不管该词语重要与否。）对于在某一特定文件里的词语来说，它的重要性可表示为：

以上式子中分子是该词在文件中的出现次数，而分母则是在文件中所有字词的出现次数之和，但是分母也可以表示成max函数，表示的是同一个意思，也就是词i出现的最多的次数（也就是所有文档中的出现次数和）。

逆向文件频率（inverse document frequency，IDF）是一个词语普遍重要性的度量（不同词重要性的度量）。某一特定词语的IDF，可以由总文件数目除以包含该词语之文件的数目，再将得到的商取对数得到：

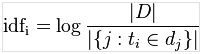
其中|D|：语料库中的文件总数：包含词语的文件数目（即的文件数目）如果该词语不在语料库中，就会导致分母为零，因此一般情况下使用 作为分母。
IDF对于common words值小，而对rare words值大。
某一特定文件内的高词语频率，以及该词语在整个文件集合中的低文件频率，可以产生出高权重的TF-IDF。因此，TF-IDF倾向于过滤掉常见的词语，保留重要的词语。
所以文本的profile是一个real vector，并且要设置一个threshold来过滤。

[ 百度百科tf-idf]

User描述User Profile

Note:
1. 这里的in是一个向量，如同上一节讲的那样。
2. simple建立一个用户profile的一个图示(不过这里还没加上weight)

用户profile建立示例

注意用户的profile不是喜欢某个item，而是item向量中的某个profile，如actor。就是说item vec中的元素是profile(e.g actor)，user vec中的元素也是profile(e.g actor)。不要跟之后要讲到的协同过滤弄混了。
用户的profile是基于评分过的item profile建立的。
示例1：Boolen Utility Matrix

这个实际就是上面的simple方式
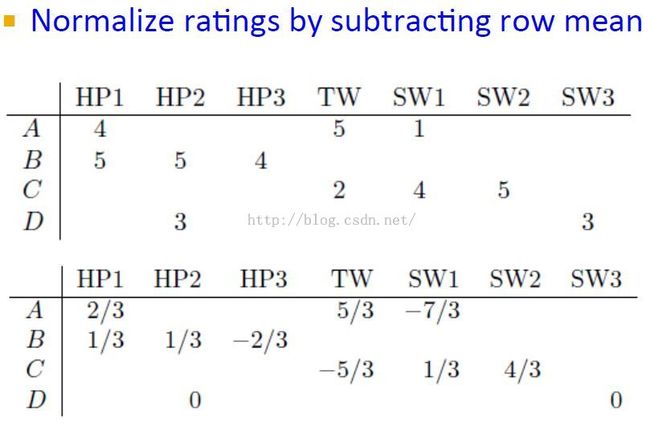
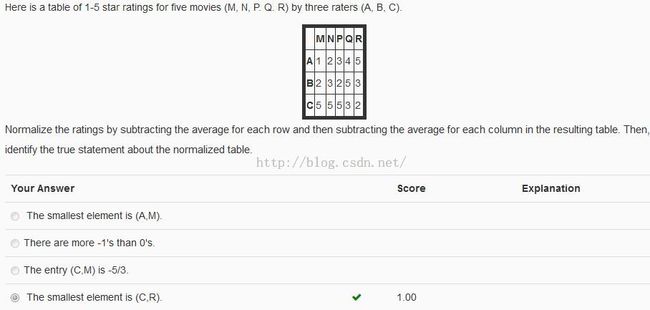
示例2：Star Ratings

由于每个user的慷慨程度不同，打分的出手值不同，需要规格化。通过规格化发现评分1 和2实际上是negative ratings。
规格化就相当于将item vec的每个属性进行了一个规格化，这种规格化是通过这个属性的所有item进行的。
注意profile的均值计算是用户对所有电影评分总分的均值，而profile A的计算是(0+2)/profile A在电影中出现的次数，而不是用户评分的所有电影总数。这种方式有效的一个直觉知识是：每个Item中的profile评分都减去了总体均值，去除了不同用户的慷慨程度影响，而除以profile在电影中出现的次数相当于再计算一次个体均值，更好拟合对某个profile的偏好程序。

推荐Making Predictions

使用余弦相似度来度量user profile和item profile的相似度，因为它适合高维度向量的相似度计算，且cosin值越大越相似（此时角度就越小）。其它度量方法见[ 距离和相似性度量方法]。

这样，我们就计算用户x的catlog中所有item i进行相似度计算，推荐给用户相似度高的items。

评价：基于内容推荐的优缺点pros and cons

优点

1. 意味着you can start working making content-based recommendations from day one for your very first user.
2. 协同过滤对于口味独特的用户可能找不到相似用户，而基于内容的推荐仍然可以推荐。when we get to collaborative filtering,We need to find similar users.But if the user were very unique or idiosyncratic taste there may not be any other similar users.But the content-based approach, user can very unique tastes as long as we can build item profiles for the items that the user likes.
3. 新来item一来就可以作推荐，它的推荐是基于其本身特征，而不是其它用户对其的评分。没有协同过滤的first-rater问题。

缺点

如果用户从未评分过某种类型的item，那么那种item也永远不会被推荐给用户，即使那个item在当前是相当受欢迎的。
皮皮blog

协同过滤Collaborative Filtering

{Collaborative Filtering, the techniques for using one person's behavior to predict what other people will do. The canonical example is the "Netflix Challenge," where it was desired to predict whether one person would like a particular movie based on the preferences of people with similar tastes.}

协同过滤就是基于邻域的算法，分为基于用户的协同过滤算法UserCF和基于物品的协同过滤算法ItemCF。

基于用户的协同过滤算法UserCF

主要思想User-user collaborative filtering

对于一个用户x，首先找到与其相似的一个用户集，这个相似是通过它们的评分rating来判定的，likes和dislikes越相似，他们就越相似。然后推荐这些相似用户集喜欢的items并且预测x评分最高的items给用户x。

用户相似的度量方法

用户-电影矩阵

Note: 这里A喜欢TW讨厌SW1，而C喜欢SW1讨厌TW。

Jaccard Similarity

没有考虑评分，导致相似度计算错误。

Cosine Similarity

这里将不知道的值设置为0

但是由于将缺失值设为0(从上节可以看出评分为0（最小的评分值）实际上是评分为负[参考上节：基于内容的推荐Content-based System-用户profile建立示例])，也没有揭示出A,B相似度远大于A,C相似度的直觉知识。

Centered Cosine(Pearson Correlation)

注意现在行和都为0了，也就是用户评分均值为0，>0表示喜欢，＜0表示不喜欢。缺失值当然也就设置为0，表示既不like也不dislike。

皮尔逊相关系数将缺失值设置为均值，符合没打分的要求；同时也解决了给分者的偏颇问题。tough raters:给分相对较小的，不慷慨的。easy raters:给分总是比较高的，慷慨的。

[距离和相似性度量方法]

评分预测

迭代求出与x最相似的k个用户，预测x对 这k个用户也评分过的items i 的评分

基于物品的协同过滤算法ItemCF

Item-item collaborative filtering

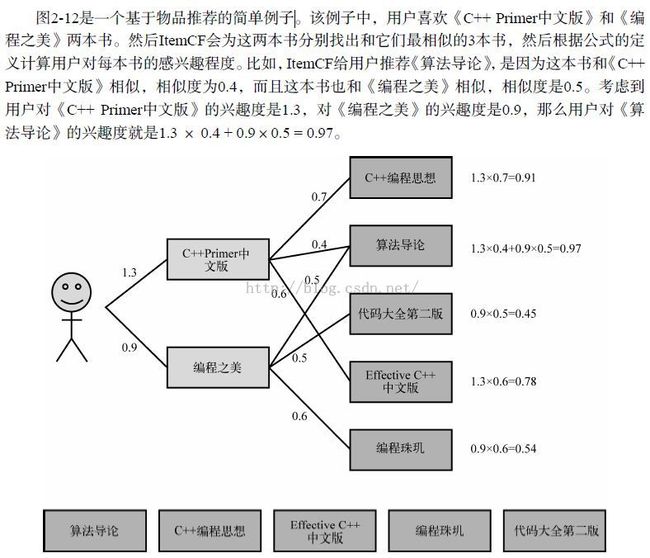
基于物品的协同过滤算法（简称ItemCF）给用户推荐那些和他们之前喜欢的物品相似的物品。比如，该算法会因为你购买过《数据挖掘导论》而给你推荐《机器学习》。不过，ItemCF算法并不利用物品的内容属性计算物品之间的相似度，它主要通过分析用户的行为记录计算物品之间的相似度。基于物品的协同过滤算法可以利用用户的历史行为给推荐结果提供推荐解释，比如给用户推荐《天龙八部》的解释可以是因为用户之前喜欢《射雕英雄传》

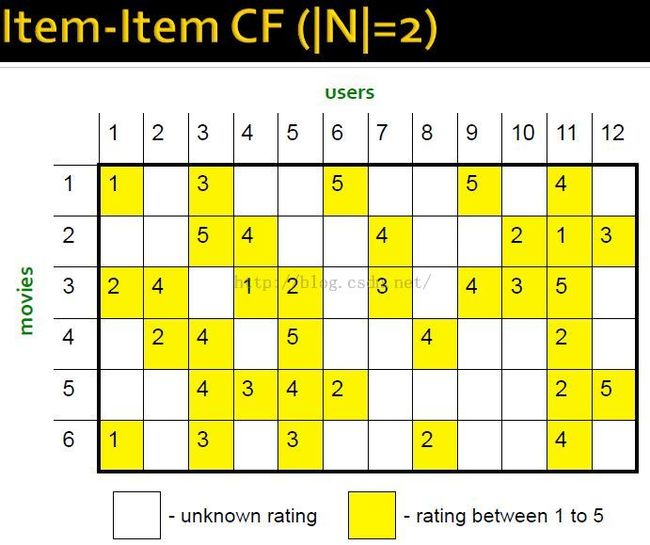
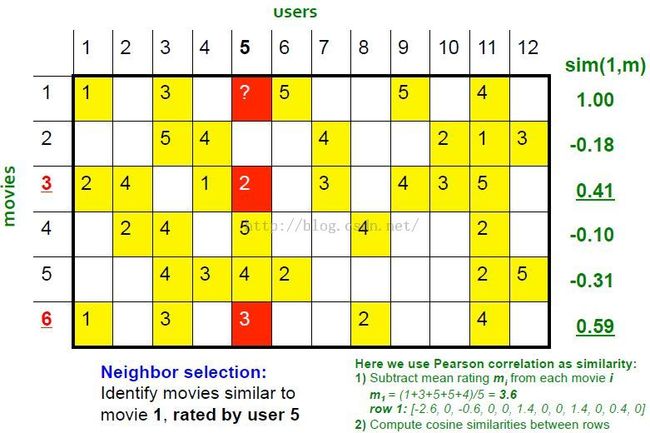
Item-Item CF示例

estimate rating of movie 1 by user 5

 

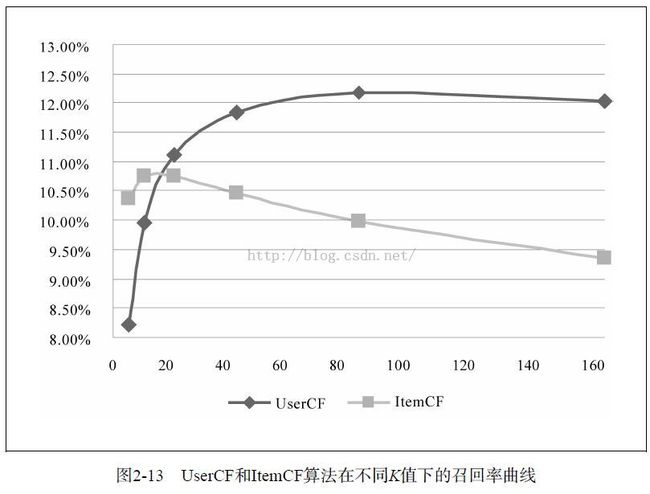
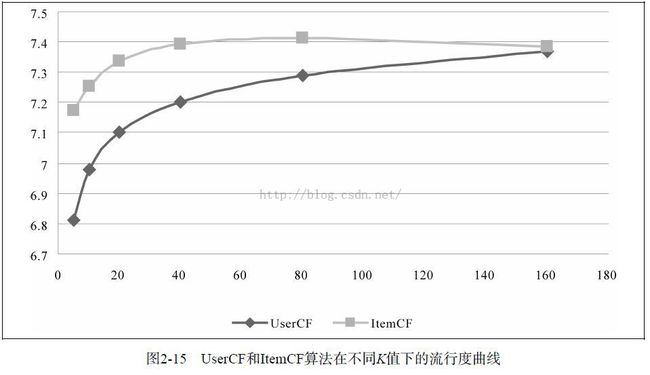
UserCF和ItemCF两种算法的比较

   

In fact, in practice item-item collaborative filtering hugely outperforms user-user collaborative filtering for most use cases.

UserCF的推荐结果着重于反映和用户兴趣相似的小群体的热点，而ItemCF的推荐结果着重于维系用户的历史兴趣。换句话说，UserCF的推荐更社会化，反映了用户所在的小型兴趣群体中物品的热门程度，而ItemCF的推荐更加个性化，反映了用户自己的兴趣传承。

个性化新闻推荐更加强调抓住新闻热点，热门程度和时效性是个性化新闻推荐的重点，而个性化相对于这两点略显次要。因此，UserCF可以给用户推荐和他有相似爱好的一群其他用户今天都在看的新闻，这样在抓住热点和时效性的同时，保证了一定程度的个性化。UserCF适合用于新闻推荐的另一个原因是从技术角度考量的。因为作为一种物品，新闻的更新非常快，每时每刻都有新内容出现，而ItemCF需要维护一张物品相关度的表，如果物品更新很快，那么这张表也需要很快更新，这在技术上很难实现。绝大多数物品相关度表都只能做到一天一次更新，这在新闻领域是不可以接受的。而UserCF只需要用户相似性表，虽然UserCF对于新用户也需要更新相似度表，但在新闻网站中，物品的更新速度远远快于新用户的加入速度，而且对于新用户，完全可以给他推荐最热门的新闻，因此UserCF显然是利大于弊。

但是，在图书、电子商务和电影网站，比如亚马逊、豆瓣、Netflix中，ItemCF则能极大地发挥优势。首先，在这些网站中，用户的兴趣是比较固定和持久的。一个技术人员可能都是在购买技术方面的书，而且他们对书的热门程度并不是那么敏感，事实上越是资深的技术人员，他们看的书就越可能不热门。此外，这些系统中的用户大都不太需要流行度来辅助他们判断一个物品的好坏，而是可以通过自己熟悉领域的知识自己判断物品的质量。因此，这些网站中个性化推荐的任务是帮助用户发现和他研究领域相关的物品。因此，ItemCF算法成为了这些网站的首选算法。此外，这些网站的物品更新速度不会特别快，一天一次更新物品相似度矩阵对它们来说不会造成太大的损失，是可以接受的。

从技术上考虑，UserCF需要维护一个用户相似度的矩阵，而ItemCF需要维护一个物品相似度矩阵。从存储的角度说，如果用户很多，那么维护用户兴趣相似度矩阵需要很大的空间，同理，如果物品很多，那么维护物品相似度矩阵代价较大。

在实际的互联网中，用户数目往往非常庞大，而在图书、电子商务网站中，物品的数目则是比较少的。此外，物品的相似度相对于用户的兴趣一般比较稳定，因此使用ItemCF是比较好的选择。当然，新闻网站是个例外，在那儿，物品的相似度变化很快，物品数目庞大，相反用户兴趣则相对固定（都是喜欢看热门的）。

 

要指出的是，离线实验的性能在选择推荐算法时并不起决定作用。首先应该满足产品的需求，比如如果需要提供推荐解释，那么可能得选择ItemCF算法。其次，需要看实现代价，比如若用户太多，很难计算用户相似度矩阵，这个时候可能不得不抛弃UserCF算法。最后，离线指标和点击率等在线指标不一定成正比。而且，这里对比的是最原始的UserCF和ItemCF算法，这两种算法都可以进行各种各样的改进。一般来说，这两种算法经过优化后，最终得到的离线性能是近似的。

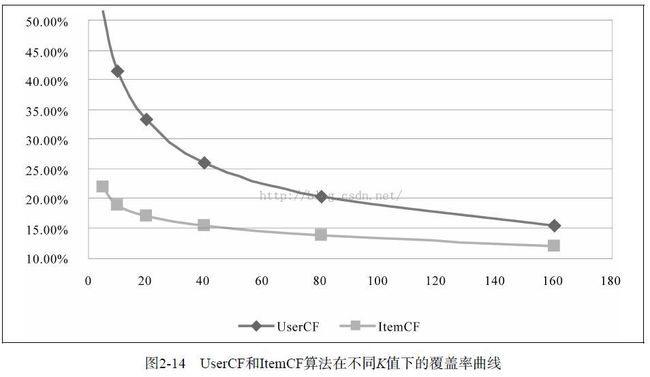
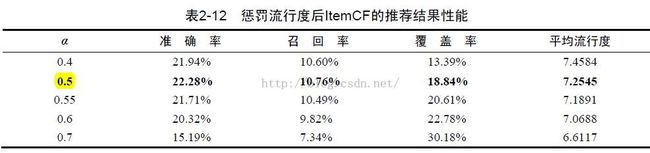
ItemCF算法的改进

原始ItemCF算法的覆盖率和新颖度都不高，这是由于哈利波特效应：

上面的问题换句话说就是，两个不同领域的最热门物品之间往往具有比较高的相似度。这个时候，仅仅靠用户行为数据是不能解决这个问题的，因为用户的行为表示这种物品之间应该相似度很高。此时，我们只能依靠引入物品的内容数据解决这个问题，比如对不同领域的物品降低权重等。这些就不是协同过滤讨论的范畴了。

皮皮blog

协同过滤的实现和改进

协同过滤复杂度分析

pre-compute的复杂度是计算item两两之间的复杂度的时间|U|，再乘以计算每个user进行推荐的用户数。

pre-compute花费时间仍旧相当高，所以就有了下面的改进策略。

改进策略

协同过滤优缺点pros&cons

Note: 最后一个缺点popularity bias可以通过加大热门item的惩罚来解决[参考上一节-ItemCF算法的改进]。

改进策略-混合方法Hybrid Methods

1. 处理新物品问题，使用物品的profiles，处理新人物问题时，使用人口统计学知识建立人物profiles。

2. 使用一个baseline算法，加上协同过滤就可以了。

Baseline与协同过滤的结合算法

整体基线估计Global Baseline Estimate

user-item矩阵稀疏性带来的一个问题

使用baseline方法估计joe对电影sixth sense的评分

Mean是所有user对所有item评分的均值。3.7 is the average rating across all movies and all users.

可以看出Joe相对来说是一个tough rater。

注意这里并没有使用joe已经评分过的电影的任何信息。

结合算法

实际上就是这两个独立分类器的线性组合

具体结合算法流程

皮皮blog

推荐系统的评估Evaluating Recommender Systems

{这里主要针对协同过滤推荐的评估}

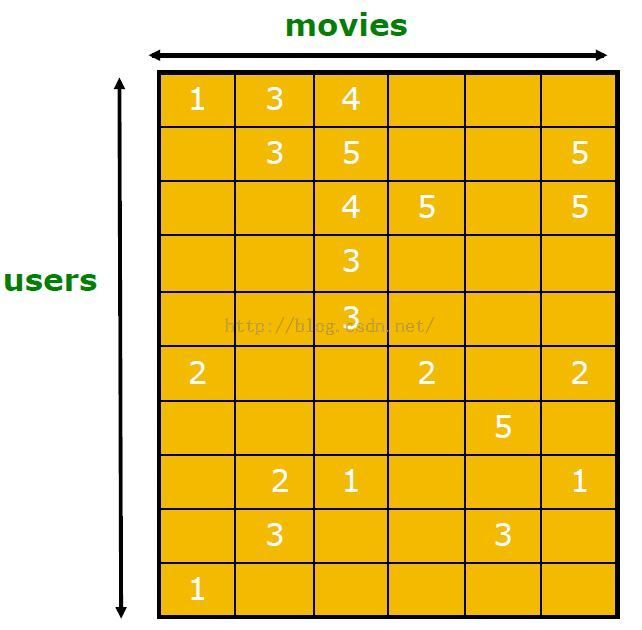
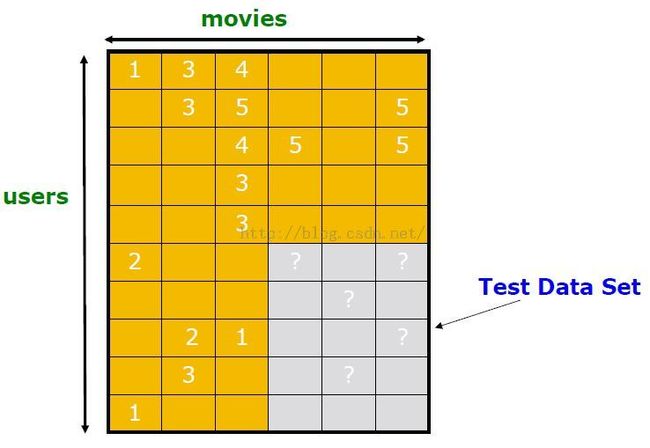
选择test data set(withheld ratings)

原始Unities矩阵

评估预测

一个更优的评估方法见下面的precision at top k方法。

误差测度问题Problem with Error Measures

1.预测多样性prediction diversity：预测的items都太相似，如对哈利波特评分高，推荐的都是哈利波特系列的电影，没有其它相关的电影。

2.预测环境prediction contexts：在法国旅游可能要推荐与法国有关的书籍，但是回国了再推荐就没有实际意义了。

3. 推荐的顺序：recommend items(movies or books) that are earlier in the sequence are ahead of items that are later in the sequence.

实际中，我们只关心高评分的预测（低评分预测根本不需要预测准确，因为低评分预测再准也没用啊，根本不会推荐预测分值低的），然而RMSE并没有对评分值高和低的items作区分，这样一来，实际中运行良好的推荐系统可能RMSE误差得分比较高。
所以选择另一种度量方法，precision at top k：在测试集（testing data/ withheld ratings）中仅仅只看给定用户评分最高的k个分数。

皮皮blog

Reviews复习

规格化问题

计算出规格化后的矩阵为：

[[-1.333 -1.     0.     0.333  2.   ]
 [-0.333  0.    -1.     1.333  0.   ]
 [ 1.667  1.     1.    -1.667 -2.   ]]

Content-based的cosin距离计算问题

Note: 距离越小越相似。

计算得到的距离矩阵分别为：

scale_alpha = 0          scale_alpha = 0.5           scale_alpha = 1                scale_alpha = 2
    A        B        C            A        B        C                   A        B        C                A        B        C
[[ 0.     0.333  1.   ]        [[ 0.     0.278  0.711]     [[ 0.     0.153  0.383]      [[ 0.     0.054  0.135]
 [ 0.333  0.     0.592]     [ 0.278  0.     0.333]      [ 0.153  0.     0.15 ]        [ 0.054  0.     0.047]
 [ 1.     0.592  0.   ]]        [ 0.711  0.333  0.   ]]     [ 0.383  0.15   0.   ]]       [ 0.135  0.047  0.   ]]

Code:

import numpy as np
from scipy import spatial

from Utility.PrintOptions import printoptions


def Nomalize(A):
    '''
    user-item规格化：对每个元素先减行和，再减列和
    '''
    row_mean = np.mean(A, 1).reshape([len(A), 1])  # 进行广播运算
    A -= row_mean

    col_mean = np.mean(A, 0)
    A -= col_mean
    with printoptions(precision=3):
        print(A)
    return A


def CosineDist(A, scale_alpha):
    '''
    计算行向量间的cosin相似度
    '''
    A[:, -1] *= scale_alpha
    cos_dist = spatial.distance.squareform(spatial.distance.pdist(A, metric='cosine'))
    with printoptions(precision=3):
        print('scale_alpha = %s' % scale_alpha)
        print('\tA\t\tB\t\tC')
        print(cos_dist)
        print()


if __name__ == '__main__':
    task = 2
    if task == 1:
        A = np.array([[1, 2, 3, 4, 5], [2, 3, 2, 5, 3], [5, 5, 5, 3, 2]], dtype=float)
        Nomalize(A)
    else:
        for scale_alpha in [0, 0.5, 1, 2]:
            A = np.array([[1, 0, 1, 0, 1, 2], [1, 1, 0, 0, 1, 6], [0, 1, 0, 1, 0, 2]], dtype=float)
            CosineDist(A, scale_alpha=scale_alpha)

from:http://blog.csdn.net/pipisorry/article/details/49205589

ref:Machine Learning - XVI. Recommender Systems 推荐系统(Week 9)

书：《推荐系统实践》-项亮