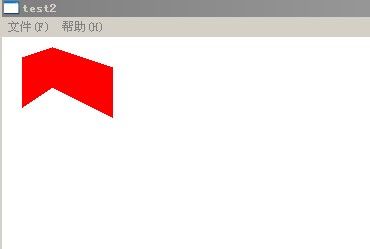
区域填充之扫描线算法

        区域的填充可以根据区域的填充，采用不同的填充算法，而其中有扫描线类算法和种子填充算法。这里，先介绍扫描线类算法之有序边表的扫描线算法。其他什么种子填充、边界标志算法、4连通区域的递归算法、8连通区域的递归算法、扫描线种子填充算法比较简单。

        其实有序边表其实领会了也好理解，关键是将思想转化为代码。

        先介绍算法思想：

        1.根据给出的多边形顶点坐标，建立ET表（同时计算ymax和ymin）

        2.初始化AET表，使之为空

        3.使用扫描线yi值作为循环变量，使之初始值为ymin

               重复做以下操作：

                  （1）如果ET表中yi桶非空，则合并到AET中

                  （2）对AET表中记录按x值从小到大排序

                  （3）依次取出表中记录，两两配对填充

                  （4）如果AET表中某记录的ymax=yi,则删除该记录

                  （5）对仍在AET中的记录，修改x值，x=x+1/m (m为斜率)

       现在，关键要细节的处理与代码实现。

       1.顶点坐标，由于无法确定顶点数，所以我们用一个数组保存。创建一个填充函数

          void regionfill(HDC hdc,Point1 *p,int len,int ymin,int ymax)  

          我们需要创建EdgeTable类，通过分析，这个结构很像我们数据结构的图（邻接表表示）

          代码如下：

/*
 *author qyl
 *date 2012/4/7
 *purpose 边表结构
 *version 1.1
 */

#include"LList.h"
#include"Point1.h"

class Edge{
public:
	float x;
	float increment;
	float ymax;

	Edge(){x=-1;increment=0;ymax=-1;}
	Edge(float x0,float incr,float y0)
	{
		x=x0;
		increment=incr;
		ymax=y0;
	}

	friend bool operator<(Edge &a,Link<Edge> &b)
	{
		return a.x<b.element.x;
	}

	friend bool operator>(Edge &a,Edge &b)
	{
		return a.x>b.x;
	}
};


class EdgeTable
{
private:
	int numberLine;
	int numberEdge;
	LList<Edge> **vertex;
public:
	EdgeTable(int numLine)
	{
		int i;
		numberLine=numLine;
		numberEdge=0;
		vertex=(LList<Edge>**) new LList<Edge>*[numberLine];
		for(i=0;i<numberLine;i++)
			vertex[i]=new LList<Edge>();
	}

	~EdgeTable()
	{
		for(int i=0;i<numberLine;i++)
			delete [] vertex[i];
		delete [] vertex;
	}

	int numberLines(){return numberLine;}
	int numberEdges(){return numberEdge;}

	bool isEmptyInLine(int pos)
	{
		return vertex[pos]->isEmpty();
	}

	LList<Edge>* getValue(int pos)
	{
		Edge it;
		LList<Edge>* l=new LList<Edge>();
		for(vertex[pos]->setStart();vertex[pos]->getValue(it);vertex[pos]->next())
		{
			l->insert(it);
		}
		return l;
	}



	void setEdge(int pos,Edge e)
	{
		Edge curr;
		for(vertex[pos]->setStart();vertex[pos]->getValue(curr);vertex[pos]->next())
		{
			if(curr.x<=e.x)
				break;
		}
		numberEdge++;
		vertex[pos]->insert(e);
	}

	void delEdge(int pos,Edge e)
	{
		Edge curr;
		for(vertex[pos]->setStart();vertex[pos]->getValue(curr);vertex[pos]->next())
		{
			if(curr.ymax==e.ymax)
			{
				vertex[pos]->remove(curr);
				numberEdge--;
			}
		}
	}

	void deleteAll(int pos)
	{
		numberEdge-=vertex[pos]->removeAll();
	}

	void createTableEdge(Point1 * p,int len,int ymin,int ymax)
	{
		Edge* e;

		/*version 1.2
		 *改进版本
		 */
		//计算各个顶点是否为奇异点,对每个顶点进行标记
		/*
		int *flag=new int[len];
	    for(int i=0;i<len;i++)
		{
			if(i==0)
			{
				if(p[1].getY()>p[0].getY() && p[len-1].getY()>p[0].getY())
					*(flag+i)=2;
				else if(p[1].getY()<p[0].getY() && p[len-1].getY()<p[0].getY())
					*(flag+i)=0;
				else if(p[1].getY()<p[0].getY() && p[len-1].getY()>p[0].getY())
					*(flag+i)=1;
				else if(p[(i+1)%len].getY()>p[i].getY() && p[len-1].getY()<p[i].getY())
					*(flag+i)=3;
			}
			else
			{
				if(p[(i+1)%len].getY()>p[i].getY() && p[(i-1)%len].getY()>p[i].getY())
					*(flag+i)=2;
				else if(p[(i+1)%len].getY()<p[i].getY() && p[(i-1)%len].getY()<p[i].getY())
					*(flag+i)=0;
				else if(p[(i+1)%len].getY()<p[i].getY() && p[(i-1)%len].getY()>p[i].getY())
					*(flag+i)=1;
				else if(p[(i+1)%len].getY()>p[i].getY() && p[(i-1)%len].getY()<p[i].getY())
					*(flag+i)=3;

			}
		}

		int mark;
		for(int i=ymin;i<=ymax;i++)
		{
			for(int j=0;j<len;j++)
			{
				if(i==(int)p[j].getY())
				{	
					mark=*(flag+j);
					if(j==0)
					{
						switch(mark)
					    {
					        case 0:   break;
					        case 1:   
								if((*(flag+len-1))!=1 && (*(flag+len-1))!=3)
								{
									e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY());
						            vertex[i]->insert(*e);
								}
								else
								{
									e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY()-1);
						            vertex[i]->insert(*e);
								}
						        break;
					        case 2:
								if((*(flag+len-1))!=1 && (*(flag+len-1))!=3)
								{
									e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY());
						            vertex[i]->insert(*e);
								}
								else
								{
									e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY()-1);
						            vertex[i]->insert(*e);
								}

								if((*(flag+j+1))!=1 && (*(flag+j+1)!=1)!=3)
								{
									e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
						            vertex[i]->insert(*e);
								}
								else
								{
									e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
						            vertex[i]->insert(*e);
								}
						         
						        break;
					       case 3:
							   if((*(flag+j+1))!=1 && (*(flag+j+1))!=3)
							   {
								   e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
						           vertex[i]->insert(*e);
							   }
							   else
							   {
								   e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
						           vertex[i]->insert(*e);
							   }
						        
						       break;
					       default:  break;
						}
					}
					else
					{
						switch(mark)
					    {
					        case 0:   break;
					        case 1:   
								if((*(flag+j-1))!=1 && (*(flag+j-1))!=3)
								{
									e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[j-1].getY());
						            vertex[i]->insert(*e);
								}
								else
								{
									e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[j-1].getY()-1);
						            vertex[i]->insert(*e);
								}
						        break;
					        case 2:
								if((*(flag+(j+1)%len))!=1 && (*(flag+(j+1)%len))!=3)
								{
									e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
					                vertex[i]->insert(*e);
								}
								else
								{
									e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
					                vertex[i]->insert(*e);
								}
					            
								if((*(flag+j-1))!=1 && (*(flag+j-1))!=3)
								{
									e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[j-1].getY());
						            vertex[i]->insert(*e);
								}
								else
								{
									e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[j-1].getY()-1);
						            vertex[i]->insert(*e);
								}
						        
						        break;
					       case 3:
							   if((*(flag+(j+1)%len))!=1 && (*(flag+(j+1)%len))!=3)
							   {
								    e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
						            vertex[i]->insert(*e);
							   }
							   else
							   {
								    e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
						            vertex[i]->insert(*e);
							   }
						       
						       break;
					       default:  break;
					    }
					}
					
				}
			}
		}
		*/


		/*
		for(int i=ymin;i<=ymax;i++)
		{
			for(int j=0;j<len;j++)
				if(i==(int)p[j].getY())
				{
					if(j==0)
					{
						//注意不能为整型 不然小数就没了

						if(p[1].getY()>p[0].getY() && p[len-1].getY()>p[0].getY())
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
							vertex[i]->insert(*e);
							e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY()-1);
							vertex[i]->insert(*e);
						}
						//非极值点 ymax-1
						else if(p[1].getY()>p[0].getY() && p[len-1].getY()<p[0].getY())
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
							vertex[i]->insert(*e);
						}
						//非极值点 ymax-1
						else if(p[1].getY()<p[0].getY() && p[len-1].getY()>p[0].getY())
						{
							e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY()-1);
							vertex[i]->insert(*e);
						}
					}
					else
					{
						
						if(p[(j+1)%len].getY()>p[j].getY() && p[(j-1)%len].getY()>p[j].getY())
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
							vertex[i]->insert(*e);
							e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY()-1);
							vertex[i]->insert(*e);
						}
						//非极值点 ymax-1
						else if(p[(j+1)%len].getY()>p[j].getY() && p[(j-1)%len].getY()<p[j].getY())
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
							vertex[i]->insert(*e);
						}
						//非极值点 ymax-1
						else if(p[(j+1)%len].getY()<p[j].getY() && p[(j-1)%len].getY()>p[j].getY())
						{
							e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY()-1);
							vertex[i]->insert(*e);
						}
					}
				}
		}
	*/
	  
		/*
		for(int j=0;j<len;j++)
		{
			int i=p[j].getY();
			if(j==0)
			{
			//注意不能为整型 不然小数就没了
				if(p[1].getY()>p[0].getY() && p[len-1].getY()>p[0].getY())
				{
					e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
					vertex[i]->insert(*e);
					e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY()-1);
					vertex[i]->insert(*e);
				}
				//非极值点 ymax-1
				else if(p[1].getY()>p[0].getY() && p[len-1].getY()<p[0].getY())
				{
					e=new Edge(p[len-1].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[0].getY()-1);
					vertex[(int)p[len-1].getX()]->insert(*e);
				}
				//非极值点 ymax-1
				else if(p[1].getY()<p[0].getY() && p[len-1].getY()>p[0].getY())
				{
					e=new Edge(p[1].getX(),(p[1].getX()-p[j].getX())/(p[1].getY()-p[j].getY()),p[1].getY()-1);
					vertex[(int)p[1].getY()]->insert(*e);
				}
			}
			else
			{		
				if(p[(j+1)%len].getY()>p[j].getY() && p[(j-1)%len].getY()>p[j].getY())
				{
					e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
					vertex[i]->insert(*e);
					e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY()-1);
					vertex[i]->insert(*e);
				}
				//非极值点 ymax-1
				else if(p[(j+1)%len].getY()>p[j].getY() && p[(j-1)%len].getY()<p[j].getY())
				{
					e=new Edge(p[(j-1)%len].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[j%len].getY()-1);
					vertex[(int)p[(j-1)%len].getY()]->insert(*e);
				}
				//非极值点 ymax-1
				else if(p[(j+1)%len].getY()<p[j].getY() && p[(j-1)%len].getY()>p[j].getY())
				{
					e=new Edge(p[(j+1)%len].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
					vertex[(int)p[(j+1)%len].getX()]->insert(*e);
				}
			}
		}
		*/

    for(int i=ymin;i<=ymax;i++)
	{
		for(int j=0;j<len;j++)
			if(i==(int)p[j].getY())
			{
				if(j==0)
				{
		//注意不能为整型 不然小数就没了

					if(p[1].getY()>p[0].getY() && p[len-1].getY()>p[0].getY())
					{
						if(p[2].getY()>p[1].getY())
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
						    vertex[i]->insert(*e);
						}
						else
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
						    vertex[i]->insert(*e);
						}
						
						if(p[len-2].getY()>p[len-1].getY())
						{
							e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY()-1);
						    vertex[i]->insert(*e);
						}
						else
						{
							e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY());
						    vertex[i]->insert(*e);
						}
						
					}
		//非极值点 ymax-1
					else if(p[1].getY()>p[0].getY() && p[len-1].getY()<p[0].getY())
					{
						if(p[2].getY()>p[1].getY())
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
						    vertex[i]->insert(*e);
						}
						else
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
						    vertex[i]->insert(*e);
						}	
					}
		//非极值点 ymax-1
					else if(p[1].getY()<p[0].getY() && p[len-1].getY()>p[0].getY())
					{
						if(p[len-2].getY()>p[len-1].getY())
						{
							e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY()-1);
						    vertex[i]->insert(*e);
						}
						else
						{
							e=new Edge(p[j].getX(),(p[len-1].getX()-p[j].getX())/(p[len-1].getY()-p[j].getY()),p[len-1].getY());
						    vertex[i]->insert(*e);
						}
						
					}
				}
				else
				{
						
					if(p[(j+1)%len].getY()>p[j].getY() && p[j-1].getY()>p[j].getY())
					{
						if(p[(j+2)%len].getY()>p[(j+1)%len].getY())
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
						    vertex[i]->insert(*e);
						}
						else
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
						    vertex[i]->insert(*e);
						}
						
						if(j==1)
						{
							if(p[len-1].getY()>p[j-1].getY())
							{
								e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY()-1);
						        vertex[i]->insert(*e);
							}
							else
							{
								e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY());
						        vertex[i]->insert(*e);
							}
						}
						else
						{
							if(p[j-2].getY()>p[j-1].getY())
							{
								e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY()-1);
						        vertex[i]->insert(*e);
							}
							else
							{
								e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY());
						        vertex[i]->insert(*e);
							}
						}
						
					}
				//非极值点 ymax-1
					else if(p[(j+1)%len].getY()>p[j].getY() && p[(j-1)%len].getY()<p[j].getY())
					{
						if(p[(j+2)%len].getY()>p[(j+1)%len].getY())
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY()-1);
						    vertex[i]->insert(*e);
						}
						else
						{
							e=new Edge(p[j].getX(),(p[(j+1)%len].getX()-p[j].getX())/(p[(j+1)%len].getY()-p[j].getY()),p[(j+1)%len].getY());
						    vertex[i]->insert(*e);
						}
						
					}
				//非极值点 ymax-1
					else if(p[(j+1)%len].getY()<p[j].getY() && p[(j-1)%len].getY()>p[j].getY())
					{
						if(j==1)
						{
							if(p[len-1].getY()>p[j-1].getY())
							{
								e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY()-1);
						        vertex[i]->insert(*e);
							}
							else
							{
								e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY());
						        vertex[i]->insert(*e);
							}
						}
						else
						{
							if(p[j-2].getY()>p[j-1].getY())
							{
								e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY()-1);
						        vertex[i]->insert(*e);
							}
							else
							{
								e=new Edge(p[j].getX(),(p[(j-1)%len].getX()-p[j].getX())/(p[(j-1)%len].getY()-p[j].getY()),p[(j-1)%len].getY());
						        vertex[i]->insert(*e);
							}
						}
					}
				}
			}
		}
		

	}



};

代码有些凌乱， 但有些错误的我并没有删去，只是展示如何一步一步改进的，以及发现的错误，改了之后好像有些注释也为修改.

这个表结构成了话，其实其他的就简单了

这个函数就是扫描线算法啦。

void regionfill(HDC hdc,Point1 *p,int len,int ymin,int ymax)
{
	EdgeTable ET(/*ymax-ymin+1*/1024);
	//创建ET表
	ET.createTableEdge(p,len,ymin,ymax);
	//初始化AET表
	EdgeTable AET(1024);
	LList<Edge>* l,*ptr;
	for(int i=ymin;i<=ymax;i++)
	{
	//如果ET表中i桶非空，将该桶中全部记录合并到AET表中
	    if(!ET.isEmptyInLine(i))
		{
			Edge curr;
			l=ET.getValue(i);
			for(l->setStart();l->getValue(curr);l->next())
			{
			    AET.setEdge(i,curr);
			}
			l->removeAll();
		}
	//在AET表中按从小到大排序
		Edge curr;
		Edge temp;
		Edge min;
		
		ptr=l=AET.getValue(i);
		/*
		AET.deleteAll(i);
		int count=0;
		for(l->setStart();l->getValue(curr);l->next())
		{
			min=curr;
			for(ptr->setPos(count);ptr->getValue(curr);ptr->next())
			{
				if(min.x>curr.x)
					min=curr;
			}
			count++;
			AET.setEdge(i,min);
		}
		*/

	//依次取出AET表中扫描线y桶中记录，两两配对填充
		
		
		for(l->setStart();l->getValue(curr);l->next())
		{
			l->next();
			l->getValue(temp);
			for(int x0=int(curr.x);x0<=temp.x;x0++)
				SetPixel(hdc,x0,i,255);
	//如果AET表中某记录的ymax=扫描线y，则删除该记录
			if(curr.ymax==i)
				AET.delEdge(i,curr);
			if(temp.ymax==i)
				AET.delEdge(i,temp);
			}
	//在AET表中的每个记录 对x进行修改
		    ptr->removeAll();
			ptr=AET.getValue(i);
			for(ptr->setStart();ptr->getValue(curr);ptr->next())
			{
				curr.x+=curr.increment;
				AET.setEdge(i+1,curr);
			}
			//填充完后 删除AET当前扫描线及l,ptr
			AET.deleteAll(i);
			l->removeAll();
			ptr->removeAll();
		}
}

       最后，谈谈细节问题。就是扫描线与顶点相交，必须正确的进行交点个数的计算，否则会出错。这个我已经包含到EdgeTable类中了，上面给出了两种思路，但其中一种由于时间问题为全部完成，已被注释掉了，有兴趣可以修改哈，代码共享哈。由于顶点前后连接构成环，而我用的数组，所以对一些特殊情况要注意，当然也可以用循环链表。

对于求最大最小值，也可以建一个函数求解，这里为了简便，采用手动输入。还有指针一定要小心。可能上面我说要排序，但我没有排序，那是我插入记录就是按排序插入的。

        因为一个大括号而多了100多的错误，因为一个变量折腾到凌晨一点……

        最后的最后，我只想说，调bug是件考验毅力耐力的活！！！

附：代码下载：http://download.csdn.net/my