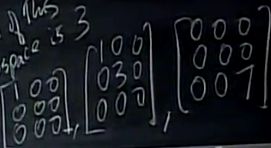线性代数导论10——四个基本子空间
本文是Gilbert Strang的线性代数导论课程笔记。课程地址: http://v.163.com/special/opencourse/daishu.html
第十课时:四个基本子空间
Am×n,列空间C(A),零空间N(A),行空间C(A
T),A转置的零空间(通常叫左零空间),线性代数的核心内容,研究这四个基本子空间及其关系
零空间N(A)
n维向量,是Ax=0的解,所以N(A)在R
n里。
列空间C(A)
列向量是m维的,所以C(A)在R
m里。
行空间C(AT)
A的行的所有线性组合,即A转置的列的线性组合(因为我们不习惯处理行向量),C(A
T)在R
n里。
A转置的零空间N(AT)—A的左零空间
N(A
T)在R
m里。
可以画出四个子空间如下,
行空间和零空间在Rn里,他们的维数加起来等于n,列空间和左零空间在Rm里,他们的维数加起来等于m。
如何分别构造他们的一组基basis?维数是多少dimension?
维数问题:
列空间:A的主列就是列空间的一组基,dim(C(A))=Rank(A)=r,维数就是秩的大小
行空间:有一个重要的性质:行空间和列空间维数相同,都等于秩的大小
零空间:一组基就是一组特殊解,r是主变量的个数,n-r是自由变量的个数,零空间的维数等于n-r
左零空间:维数为m-r。
n维空间中存在两个子空间,一个r维的行空间,一个n-r维的零空间,维数和为n。和另一个结论相似:r个主变量,n-r个是自由变量,加起来是n。
m维空间中存在两个子空间,一个r维的列空间,一个m-r维的左零空间,维数和为m。
基的问题:
列空间:主列组合就是一组基
零空间:一组特殊解就是一组基
行空间:通过初等行变换变换成行最简式,行空间的一组基即是行最简形R的前r(秩数)行。(
行变换不会对行空间产生影响,但会对列空间产生影响。)
如上图,A通过初等行变换得到R,前两行就是行空间的一组基,为什么说它们一定在矩阵的行空间里?因为行变换的时候是某行和令一行相加或相减,即是这些行向量的的线性组合。
左零空间(A转置的零空间):为什么叫左零空间?
A
Ty=0,将等式左右两边都转置,得:y
TA=0
T,如下,所以叫左零空间。
但我们一般还是习惯用A
Ty=0,因为希望y是列向量。
求矩阵的左零空间,就试着寻找一个产生零行向量的行组合,求矩阵的零空间,就试着寻找一个产生零列向量的列组合。
如上,求A得左零空间,通过行变换得到R,R的最后一行是0向量,行变换的逆变换E的最后一行即是A的各行的组合产生0向量的向量。即,左零空间的一组基为[-1,0,1]
下一节课预告:新的向量空间,所有的3*3矩阵,把矩阵看着“向量”,每个3*3的矩阵都是一个“向量“,叫他们为向量,因为他们服从向量加法,乘法,又能够对矩阵进行线性组合...。向量空间,关心的是A+B和cA。子空间比如上三角矩阵,对称矩阵,子空间的交集也是子空间。关注他们的维数,基。3*3的对角矩阵的维数为3,一组基为
认为
这三个矩阵相互线性无关,而且任何的对角矩阵可通过这三个组合得到,因此他们生成了对角矩阵空间。我们把Rn的概念延伸至Rn*n,他们仍对加法和乘法封闭。