Chapter 3 | Stacks and Queues--一个数组实现三个栈
3.1 Describe how you could use a single array to implement three stacks.
译文:如何只用一个数组实现三个栈
栈的一大特性是“先进后出”,所以一般而言,我们把具备这种特性的数据结构称之为栈(严格来说似乎有点牵强)。
方法一:可以很快速的用一个数组实现一个栈,题目要求实现三个栈,自然地,我们可以把这个数组截成三段,每段实现一个栈,这里是数组存储元素,所以生成的栈自然是线性栈。
这里与常规的栈的实现有点不一样,不需要单独初始化一个栈结构,直接对给定数组压入元素弹出元素即可,但栈顶指针,栈长度还是需要指定的
在没有特殊要求下,我们可以把数组平均的截成三段,这样每个栈的长度大致是一样的,而且这三个栈是呈线性连接的,反过来,也可以指定每个栈相同的长度值,然后连成一个数组。这样每个栈隐性的维护一个栈顶指针和栈长度,每压入一个值,栈顶指针加1,栈长度加1,出栈就对应相减,并返回栈顶元素。
需要稍加考虑的是临界情况,栈为空时,栈顶指针设置为-1(数组从0开始),非空时,栈顶指针时刻指向栈顶元素。可以设置三个栈区分别为
》》stack1:[ 0, stackSize )
》》stack2:[ stackSize, 2*stackSize )
》》stack3:[ 2*stackSize, 3*stackSize )
详见代码:
int stackSize = 100;
int *buffer = (int *)malloc(stackSize * 3 * sizeof(int)); //数组
int stackPointer[] = { -1, -1, -1 }; //初始情况,偏移栈顶“指针”,数组元素维护,非真正意义上的栈顶指针
int stackLength[] = { 0, 0, 0 }; //栈长度
bool push(int stackNum, int value)
{
if (stackLength[stackNum] == stackSize)
return false;
/*实际栈顶“指针”*/
int index = stackNum * stackSize + stackPointer[stackNum] + 1;
stackPointer[stackNum]++;
buffer[index] = value;
stackLength[stackNum]++;
return true;
}
bool pop(int stackNum, int *value)
{
if (0 == stackLength[stackNum])
return false;
int index = stackNum * stackSize + stackPointer[stackNum];
stackPointer[stackNum]--;
*value = buffer[index];
stackLength[stackNum]--;
return true;
}
bool isEmpty(int stackNum)
{
return (0 == stackLength[stackNum]);
}
bool isFull(int stackNum)
{
return (stackLength[stackNum] == stackSize);
}上面这个方法有一个弊端,单个栈区不可扩容,也就是每个栈一开始就指定了固定长度,如果某个栈需要大于100的容量就会溢出。
方法二:上面是给数组里面存放数据,顺序栈。我们可以在数组里面存放栈结构,该结构里面维护当前栈顶位置和栈顶的前一个位置,通过这样一个变式的链式方式来维护一个栈,这样每个栈并不要求是连续的,通过栈顶的前一个位置去指定出栈后的栈顶位置,同样也不需要指定每个栈空间长度,总长度不超出数组空间,就不会发生溢出情况。
其余分析详见代码注释
typedef struct _Stack
{
int value; //当前元素
int preIndex; //上一个元素的索引
}Stack;
int totalSize = 300;
int stackPointer[] = { -1, -1, -1 };
int indexUsed = 0;
Stack *buffer = new Stack[totalSize];
/*
每个栈必须维护其各自的栈顶位置以及其栈顶的前一个位置,
后者保证出栈之后,栈顶位置时刻指向栈顶元素
*/
bool push(int stackNum, int value)
{
if (indexUsed == totalSize) //“总栈”溢出
return false;
/*第stackNum栈的前一个元素位置,就是压栈之前的栈顶位置*/
int lastIndex = stackPointer[stackNum];
stackPointer[stackNum] = indexUsed; //第stackNum栈的栈顶指针
buffer[stackPointer[stackNum]].value = value; //stackNum栈的栈顶元素
buffer[stackPointer[stackNum]].preIndex = lastIndex; //指向前一个元素的索引
//通过索引建立元素栈关系
indexUsed++; //已使用的数组空间
return true;
}
bool pop(int stackNum, int *value)
{
if (-1 == stackPointer[stackNum]) //stackNum栈空
return false;
*value = buffer[stackPointer[stackNum]].value; //返回第stackNum栈的栈顶元素
/*第stackNum栈的栈顶“指针”指向当前栈顶的前一个位置,出栈之后,该位置替换为栈顶位置*/
stackPointer[stackNum] = buffer[stackPointer[stackNum]].preIndex;
//indexUsed--; //会出现覆盖
return true;
}
bool isEmpty(int stackNum)
{
return (-1 == stackPointer[stackNum]);
}
上面程序中的 pop 函数弹出元素后,总栈长度 indexUsed 并没有减1,每次压栈indexUsed总是递增的,这就意味着存在空间的浪费,即多次出栈入栈之后,实际总栈长度会小于indexUsed。
测试程序
int main()
{
int value0, value1, value2;
for (int i = 0; i < 3; ++i)
{
if (!push(0, i) || !push(1, i+3))
break;
}
for (int i = 0; i < 3; ++i)
{
if (!pop(0, &value0))
break;
}
for (int i = 0; i < 3; ++i)
{
if (!push(2, i+6))
break;
}
for (int i = 0; i < 9; ++i)
cout << buffer[i].value << endl;
return 0;
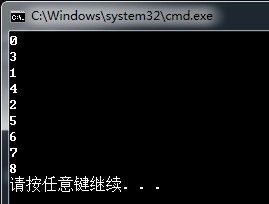
}第一个 for 循环里,两个栈压栈之后,数组空间里的元素分布为:0 , 3 , 1 , 4 , 2 , 5。其中 Stack_0 为0,1,2; Stack_1 为3,4,5。
第二个for循环,Stack_0 出栈,但是indexUsed没变,如果indexUsed减1的话,下一次压栈就会直接覆盖Stack_1的部分数据。
第三个for循环,Stack_2 压栈,indexUsed在原有基础上递增。
这样整个数组空间里的元素分布为 0 , 3 , 1 , 4 , 2 , 5 , 6 , 7 , 8 。实际上 Stack_0已经出栈了,但是其废弃元素还占据数组空间。
不过我们也有方法来避免这种空间的浪费,具体实现参见这篇博文 :一个数组实现三个栈(续)