【贪心】【Uva11729】 Commando War
你有n个部下,每个部下需要完成一项任务。第i个部下需要你花Bi分钟交待任务,然后他会立刻独立地、无间断地执行Ji分钟后完成任务。你需要选择交待任务的顺序,使得所有任务尽早执行完毕(即最后一个执行完的任务应尽早结束)。注意,不能同时给两个部下交待任务,但部下们可以同时执行他们各自的任务。
【输入格式】
输入包含多组数据,每组数据的第一行为部下的个数N(1≤N≤1 000);以下N行每行两个正整数B和J(1≤B≤10 000,1≤J≤10 000),即交待任务的时间和执行任务的时间。输入结束标志为N=0。
【输出格式】
对于每组数据,输出所有任务完成的最短时间。
【样例输入】
3
2 5
3 2
2 1
3
3 3
4 4
5 5
0
【样例输出】
Case 1: 8
Case 2: 15
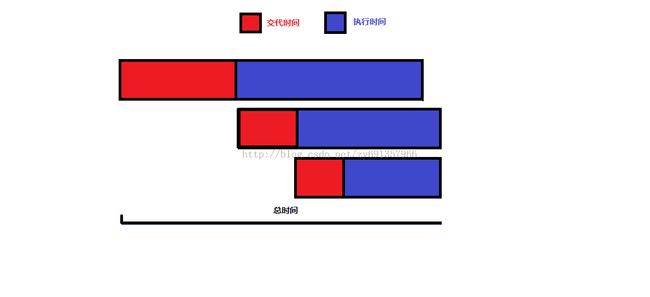
贪心先画几个图看看流程 这种线段型图很实用
显然红色时间是必须有的,总时间的长短在于蓝色的摆放
从图中情不自禁的就有感觉 蓝色长的先选即可
、
显然更优
证明
对于k1士兵 k2士兵 假设J[k1]>J[k2]
若k2 在前面 总时间为 T=(B[k2]+B[k1]+J[k1])
若k1 在前面 总时间为T=MAX(B[k1]+J[k1],B[k1]+B[k2]+J[k2])
无论MAX 选哪个 都比T要小 所以k1最好在k2前面贪心策略得证
代码如下:
#include<cstdio>
#include<algorithm>
#include<cstdlib>
using namespace std;
int CASE=0;
typedef struct node
{
int b;
int j;
}node;
node p[1010];
int cmp(const void *i,const void *k)
{
node *ii=(node *)i,*kk=(node *)k;
return kk->j-ii->j;
}
int main()
{
int N,ans,k;
// freopen("a.in","r",stdin);
// freopen("a.out","w",stdout);
while(scanf("%d",&N)!=EOF&&N!=0)
{
CASE++;
ans=0;k=0;
for(int i=1;i<=N;i++)
scanf("%d%d",&p[i].b,&p[i].j);
qsort(p+1,N,sizeof(p[0]),cmp);
for(int i=1;i<=N;i++)
{
k=k+p[i].b;
if(k+p[i].j>ans)
ans=k+p[i].j;
}
printf("Case %d: %d\n",CASE,ans);
}
return 0;
}
思考题:
若设置一个总时间T 问最多能让多少人完成任务?
需要再思考一下