Euclid NBU 1844

Euclid

Time Limit:1000MS  Memory Limit:65536K
Total Submit:49 Accepted:11

Description

In one of his notebooks, Euclid gave a complex procedure for solving the
following problem. With computers, perhaps there is an easier way.
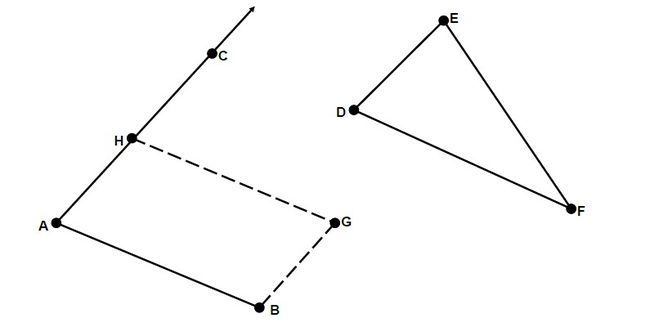
In a 2D plane, consider a line segment AB, another point C which is not collinear
with AB, and a triangle DEF. The goal is to find points G and H such that:
H is on the ray AC (it may be closer to A than C or further away, but angle
CAB is the same as angle HAB)
ABGH is a parallelogram (AB is parallel to HG, AH is parallel to BG)
The area of parallelogram ABGH is the same as the area of triangle DEF

Input

There will be several test cases. Each test case will consist of twelve real
numbers, with no more than 3 decimal places each, on a single line. Those
numbers will represent, in order:
AX AY BX BY CX CY DX DY EX EY FX FY
where point A is (AX,AY), point B is (BX,BY), and so on. Points A, B and C are
guaranteed to NOT be collinear. Likewise, D, E and F are also guaranteed to be
non-collinear. Every number is guaranteed to be in the range from -1000.0 to
1000.0 inclusive. End of the input will be signified by a line with twelve 0.0‟s.

Output

For each test case, print a single line with four decimal numbers. These represent points G and H, like this:
GX GY HX HY
where point G is (GX,GY) and point H is (HX,HY). Print all values rounded to 3 decimal places of precision (NOT truncated). Print a single space between numbers. Do not print any blank lines between answers.

Sample Input

0 0 5 0 0 5 3 2 7 2 0 4
1.3 2.6 12.1 4.5 8.1 13.7 2.2 0.1 9.8 6.6 1.9 6.7
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0

 

Sample Output

5.000 0.800 0.000 0.800
13.756 7.204 2.956 5.304

wa了n次之后，我发现三角形面积和平行四边形面积要么都用海伦公式做，要么都用叉积做，否则相除会出现精度问题错误

#include<iostream>
#include<math.h>
using namespace std;
struct Points
{
	double x,y;
}A,B,C,D,E,F,G,H;

double dis(Points a,Points b)
{
	return(sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)));
}

int main()
{
	int i,j;
	while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf",&A.x,&A.y,&B.x,&B.y,&C.x,&C.y,&D.x,&D.y,&E.x,&E.y,&F.x,&F.y)!=EOF)
	{
		if(!A.x && !A.y && !B.x && !B.y && !C.x && !C.y && !D.x && !D.y && !E.x && !E.y) break;
		double triangle,par;
		double p=0,p2=0;
		double t1=dis(D,E),tt1=dis(A,B);
		double t2=dis(D,F),tt2=dis(B,C);
		double t3=dis(E,F),tt3=dis(A,C);
		p=t1+t2+t3;p2=tt1+tt2+tt3;
		p/=2;p2 /= 2;
		triangle=sqrt(p*(p-t1)*(p-t2)*(p-t3));
		//par=(C.y-A.y)*(B.x-A.x)+(A.y-B.y)*(C.x-A.x);
		par = 2*sqrt(p2*(p2-tt1)*(p2-tt2)*(p2-tt3));
		double rate = triangle/par;
		H.x=A.x+rate*(C.x-A.x);
		H.y=A.y+rate*(C.y-A.y);

		G.x=B.x+rate*(C.x-A.x);
		G.y=B.y+rate*(C.y-A.y);

		printf("%.3lf %.3lf %.3lf %.3lf/n",G.x,G.y,H.x,H.y);
	}
}