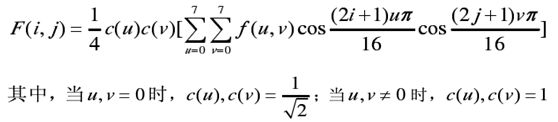JPEG解码算法流程详解

（1）读入JPEG/JFIF文件的相关信息

按照JFIF文件格式，将JPEG文件相关的字段信息一一读取出来，并进行相应的解析。例如，图像的宽度、高度、量化表、Huffman表、水平/垂直采样因子等。一般而言，JFIF格式文件的读取顺序依次为：

SOI字段；

APP0字段；

APPn字段；

DQT字段；

SOFO字段；

DHT字段；

SOS字段；

压缩数据字段；

EOI字段；

读取JPEG文件相关信息的时候，有两点需要特别注意：

（a）由于JPEG中以0XFF来做为特殊标记符，因此，如果某个像素的取值为0XFF，那么实际在保存的时候，是以0XFF00来保存的，从而避免其跟特殊标记符0XFF之间产生混淆。所以，在读取文件信息的时候，如果遇0XFF00，就必须去除后面的00；即，将0XFF00当做0XFF；

（b）JPEG文件中，一个字（16位）的存储是采用了Motorola格式（big-endian），而不是我们常用的Intel格式（little-endian）。因此，如果需要的话，请在处理之间进行依次高低字节的转换。

（2） 读取Huffman表

在标记码DHT之后，包含了一个或者多个Huffman表（通常是4个表）。对于一个Huffman表而言，它包含了以下三部分内容：

（a）表ID和表类型；1个字节；仅有4个可选的取值，0X00,0X01,0X10,0X11，分别表示DC直流0号表，DC直流1号表，AC交流0号表，AC交流1号表；

（b）不同位数的码字数量；前面提到,JPEG中的Huffman编码表是按照编码长度的位数以表格的形式保存的，而且，Huffman编码表的位数只能是1--16位，因此，这里用16个字节来分别表示1--16位的每种位长的编码在Huffman树中的个数。

（c）编码内容；该字段记录了Huffman树中各个叶子节点的权重，上一个字段（不同位数的码字数量）的16个数值之和，就是本字段的长度，也就是Huffman树中叶子节点的个数。

这里，我们不妨以下面一段Huffman表的数据为例来说明情况（均以16进制表示）：

11 00 02 02 00 05 01 06 01 00 00 00 00 00 00 00 00

00 01 11 02 21 03 31 41 12 51 61 71 81 91 22 13 32

以上数据串中第一行代表了Huffman表ID、表类型、不同位数的码字数量信息；

第一行的第一个字节0X11代表了表的ID和类型是AC交流1号表；

第一行的第2到第17字节代表了不同位数码字的数量。即，第2个字节00表示没有位数为1的编码；第3个和第4个字节的02表示位数为2和位数为3的编码各有两个；第5个字节的00表示没有位数为5的编码。。。。此外，通过这些数据我们发现，此Huffman树有0+2+2+0+5+1+6+1=17个叶子节点。

第二行为编码的内容，表明17个叶子节点按照从小到大的顺序排列，即，权值依次为0,1,11,2,21,3,31,41...

（3） 构建Huffman树

读取到Huffman表的数据之后，就需要构建Huffman树了。其具体规则如下

  （a）第一个编码的数字必定为0；如果第一个编码的位数为1，就被编码为0；如果第一个编码的位数为2，就被编码为00；如果第一个编码的位数为3，就被编码为000。。。

  （b）从第二个编码开始，如果它和它前面编码具有相同的位数，则当前编码是它前面的编码加1；如果它的编码位数比它前面的编码位数大，则当前编码时它前面的编码加1之后再在后面添加若干个0，直到满足编码位数的长度为止。

还是以上面的数据为例：

第一行的第2个字节00表示没有位数为1的编码；

第一行的第3个字节02表示位数为2的编码有2个；由于没有位数为1的编码，因此这里位数为2的编码中的第一个为00，第二个为00+1=01；

第一行的第4个字节02表示位数为3的编码有2个；因此，这里位数为3的编码中的第一个为01+1=10，然后添加1个“0”，得到100；位数为3的编码中的第二个为100+1=101；

依次类推，可以得到如下的Huffman树

序号	码字长度	码字	权值
1	2	00	0x00
2	2	01	0x01
3	3	100	0x11
4	3	101	0x02
5	5	11000	0x21
6	5	11001	0x03
7	5	11010	0x31
8	5	11011	0x41
9	5	11100	0x12
10	6	111010	0x51
11	7	1110110	0x61
12	7	1110111	0x71
13	7	1111000	0x81
14	7	1111001	0x91
15	7	1111010	0x22
16	7	1111011	0x13
17	8	11111000	0x32

特别提醒的是，如果中间有某个位数的编码缺失，例如，没有4位的编码，则应该在3位的编码后面加1，添加2个“00”补足5位，形成下一个5位编码。

 

（4） DC系数的Huffman解码

JPEG编码阶段我们讲到，DC系数是以（A,B）的中间形式进行编码的。其中的A代表了B的二进制编码位数，B则利用VLI进行编码。另外，8*8的图像块经过DCT变换之后得到的8*8的系数矩阵，经过Huffman编码及RLE编码之后，写入编码数据的时候，DC系数也是被写在数据流最前面的。因此，解码的时候，DC系数也是最先被读取出来，假设，我们一次性读入了若干个字节长度的数据。其中的第一个字节代表了DC系数的Huffman编码，通过查找DC系数的Huffman表（亮度表或色度表），得到该Huffman编码所在的组编号，该编号就是DC系数中间格式（A,B）中的A，也就是B的位数。例如，A=2，就代表B采用2位二进制数进行编码。这样一来，读取接下来的A位二进制数，将其译码为十进制，就得到了DC系数的差值。将该差值与上一个DC系数值相加，就得到了真正的当前DC系数的值。

（5） AC系数的Huffman解码

处理完DC系数之后，接下来进行AC系数的译码工作，显然，这里依然需要读取一个Huffman编码，通过查找AC系数的Huffman编码表，进行解码，我们得到(A,B)的数据对，其中的A代表了0的个数，而B则代表了后面数据的位数。例如，（2,3）就代表了当前AC系数之前有2个0，下一个需要读取的二进制数据是3位。需要提醒的是，（0,0）代表EOB，即8*8块的编码结束。接着，读取B位二进制数据，进行译码，我们就得到了AC系数的值。如此反复循环，直到遇到EOB，或者读取了63个AC系数，我们就完成了一个8*8块的系数矩阵的译码工作。

（6） 反量化

在译码得到了8*8的系数矩阵之后，我们需要进行反量化工作。该步骤，就是将前一个步骤得到的8*8系数矩阵分别乘以8*8的量化矩阵即可。

（7） 反Zig-zag扫描

JPEG编码过程中，为了编码方便，采用了Zig-zag扫描，因此，这里需要进行反Zig-zag扫描，重新排列8*8的反量化系数矩阵。反Zig-zag扫描的输入时8*8矩阵，输出依然是8*8矩阵，只不过，数据的排列方式有所不同而已。

（8） DCT逆变换

DCT变换，将原始图像变换到频域，而DCT逆变换，就是要将数据从频域变换回时域。

DCT逆变换的计算公式为：

DCT逆变换的公式，可以改写为：

其中A为矩阵：

左边为未转秩的数据顺序，右边为转秩之后的数据顺序。

（9）颜色模式转换

BMP图片是以RGB颜色空间进行保存的，因此，将JPEG解码为BMP必须进行颜色模式的转换。另外，由于DCT要求的定义域对称，所以，在编码的时候将RGB的数值范围从[0,255]统一减去128，将数值范围转换到[-128,127]的范围内。因此，解码的时候，必须为每个颜色分量加上128。另外需要注意的是，通过解码变换之后得到的RGB的值有可能超过255或者小于0；如果小于0，就截断为0，如果大于255，就截取为255；