zoj 3256 Tour in the Castle(插头DP一条回路+矩阵连乘)
After the final BOSS is defeated, the hero found that the whole castle is collapsing (very familiar scene, isn't it). Escape from the castle is easy, just need to cross a few rooms. But as the Hero is full of adventurous spirit, he decides to visit every room before he escape the castle.
The castle is a rectangle with N * M rooms in it. Two rooms are connected if they share a common edge. The hero starts in the top left room. And the bottom left room is the only way out. After the hero visits a room and leaves it, it will collapse immediately(Another familiar scene). So he can visit each room only once.
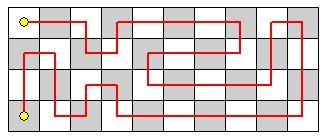
The diagram shows one tour over a castle with 4 * 10 rooms:
Input
There are multiply cases (<20), process to the end of file.
Each case contains a line with two Integer N and M (2 <= N <= 7, 1 <= M <=10^9).
Ouput
For each case, if it's impossible to visit every room exactly once and get to the bottom left room, output "Impossible". Otherwise, output the number of tours as it describe above. Beacause the answer can be huge, you just need to output the answer MOD 7777777.
Sample Input
3 2 3 3 4 10
Sample Output
Impossible 2 2329Author: WANG, Yelei
Source: ZOJ Monthly, September 2009
题目: http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3256
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int mm=66666;
const int mod=7777777;
typedef long long LL;
struct hashMap
{
int h[mm],s[mm],p[mm],t;
int push(int w)
{
for(int i=h[w];i>=0;i=p[i])
if(s[i]==w)return i;
s[t]=w,p[t]=h[w],h[w]=t;
return t++;
}
void clear()
{
t=0,memset(h,-1,sizeof(h));
}
}g,f[2];
LL a[222][222],b[222][222],c[222][222];
int i,j,k,n,m,g1,g2;
void Multi(LL a[222][222],LL b[222][222])
{
for(i=0;i<g.t;++i)
for(j=0;j<g.t;++j)
for(c[i][j]=k=0;k<g.t;++k)
{
c[i][j]+=a[i][k]*b[k][j];
if(c[i][j]>=mod)c[i][j]%=mod;
}
for(i=0;i<g.t;++i)
for(j=0;j<g.t;++j)
a[i][j]=c[i][j];
}
int Link(int s,int flag)
{
int w,n=1,x=3<<(j<<1),a=(2-flag)<<(j<<1);
while(n)
{
if(flag)a<<=2,x<<=2;
else a>>=2,x>>=2;
w=x&s;
if(w)n+=(w==a)?1:-1;
}
return s^x;
}
void Work(int s)
{
int e,w=j<<1,x=(s>>w)&15;
if(x==9)return;
if(!x)
{
if(j+1<n)f[g2].push(s^(9<<w));
}
else if(!(x&3)||!(x&12))
{
if(x&3)e=0,x|=x<<2;
else e=1,x|=x>>2;
if(!e||j+1<n)f[g2].push(s);
if(e||j+1<n)f[g2].push(s^(x<<w));
}
else if(x==6)f[g2].push(s^(x<<w));
else f[g2].push(Link(s^(x<<w),x==5));
}
void InitMatrix()
{
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
g.clear();
g.push(1|(2<<((n-1)<<1)));
for(i=0;i<g.t;++i)
{
f[0].clear();
f[0].push(g.s[i]<<2);
for(g2=j=0;j<n;++j)
for(g1=g2,g2=!g2,f[g2].clear(),k=0;k<f[g1].t;++k)
Work(f[g1].s[k]);
for(k=0;k<f[g2].t;++k)
a[g.push(f[g2].s[k])][i]=1;
b[i][i]=1;
}
}
void Solve()
{
InitMatrix();
while(m)
{
if(m&1)Multi(b,a);
Multi(a,a);
m>>=1;
}
LL ans;
for(i=0;i<g.t;++i)
if(g.s[i]==(9<<((n-2)<<1)))ans=b[i][0];
if(ans)printf("%lld\n",ans);
else puts("Impossible");
}
int main()
{
while(~scanf("%d%d",&n,&m))Solve();
return 0;
}