OpenGL中glRotatef()函数究竟对矩阵做了什么
OpenGL中glRotatef()函数究竟对矩阵做了什么
我们知道OpenGL中维持着两套矩阵,一个是模型视图矩阵(model view matrix),另一个是投影矩阵(projection matrix)。而Direct3D维持着三个矩阵,其实它们的本质是一样的,因为Model(World)矩阵×View矩阵 = ModelView矩阵,也就是OpenGL的模型视图矩阵。通过对OpenGL这两套矩阵的变换,我们可以得到各种投影效果。这回我就来研究OpenGL中一个常见的函数glRotatef(d)。
看参数,glRotatef( angle, x, y, z )函数的作用是将当前坐标系以a( x, y, z )向量为旋转轴旋转angle角度。这种方法可以以简单明白的方式将世界坐标系进行旋转。但是在内部,OpenGL究竟是用什么公式对其进行旋转呢?
原创文章,反对未声明的引用。原博客地址:http://blog.csdn.net/gamesdev/article/details/9929211
为了弄清楚真相,我们开始研究矩阵的相关知识。首先,我们考虑单位矩阵I在绕着坐标轴旋转后所得的旋转矩阵。这里我直接列出了三种情况:
知道了绕着三轴后的旋转矩阵,那么下面就是绕任意向量所得的矩阵了。设M为单位矩阵经向量a旋转后的矩阵,且a = (xa, ya, za),旋转角度为α,则M=

我其实也不明白该如何证明的,不过我们可以编写一个小程序来验证一下:
#include <assert.h>
#include <stdio.h>
#include <math.h>
#include "GLWidget.h"
void PrintMatrix( float matrix[16] )
{
assert( matrix != 0 );
printf( "%8.2f%8.2f%8.2f%8.2f\n"
"%8.2f%8.2f%8.2f%8.2f\n"
"%8.2f%8.2f%8.2f%8.2f\n"
"%8.2f%8.2f%8.2f%8.2f\n",
matrix[0], matrix[1], matrix[2], matrix[3],
matrix[4], matrix[5], matrix[6], matrix[7],
matrix[8], matrix[9], matrix[10], matrix[11],
matrix[12], matrix[13], matrix[14], matrix[15] );
}
void MyRotatef( float matrix[16],
float angleInDegree,
float x,
float y,
float z )
{
assert( matrix != 0 );
// 向量的单位化
float length = sqrt( x * x + y * y + z * z );
assert( !qFuzzyCompare( length, 0.0f ) );// 希望length不为0
x /= length;
y /= length;
z /= length;
float alpha = angleInDegree / 180 * 3.1415926;// 已转换弧度制
float s = sin( alpha );
float c = cos( alpha );
float t = 1.0f - c;
#define MATRIX( row, col ) matrix[row * 4 + col]
MATRIX( 0, 0 ) = t * x * x + c;
MATRIX( 0, 1 ) = t * x * y + s * z;
MATRIX( 0, 2 ) = t * x * z - s * y;
MATRIX( 0, 3 ) = 0.0f;
MATRIX( 1, 0 ) = t * x * y - s * z;
MATRIX( 1, 1 ) = t * y * y + c;
MATRIX( 1, 2 ) = t * y * z + s * x;
MATRIX( 1, 3 ) = 0.0f;
MATRIX( 2, 0 ) = t * x * z + s * y;
MATRIX( 2, 1 ) = t * y * z - s * x;
MATRIX( 2, 2 ) = t * z * z + c;
MATRIX( 2, 3 ) = 0.0f;
MATRIX( 3, 0 ) = 0.0f;
MATRIX( 3, 1 ) = 0.0f;
MATRIX( 3, 2 ) = 0.0f;
MATRIX( 3, 3 ) = 1.0f;
#undef MATRIX
}
GLWidget::GLWidget( QWidget* pParent ):
QGLWidget( pParent )
{
setWindowTitle( "Test OpenGL Matrix" );
}
void GLWidget::initializeGL( void )
{
float angle = 30.0f;
float x = 12.0f;
float y = 8.0f;
float z = 3.0f;
float matrix1[16], matrix2[16];
glMatrixMode( GL_MODELVIEW );
glLoadIdentity( );
glGetFloatv( GL_MODELVIEW_MATRIX, matrix1 );
glGetFloatv( GL_MODELVIEW_MATRIX, matrix2 );
printf( "The initial identity matrix is:\n" );
PrintMatrix( matrix2 );
printf( "Now perform OpenGL glRotate function.\n" );
glRotatef( angle, x, y, z );
glGetFloatv( GL_MODELVIEW_MATRIX, matrix1 );
PrintMatrix( matrix1 );
printf( "Now perform MyRotate function.\n" );
MyRotatef( matrix2, angle, x, y, z );
PrintMatrix( matrix2 );
}
void GLWidget::paintGL( void )
{
}
程序的运行结果如下:
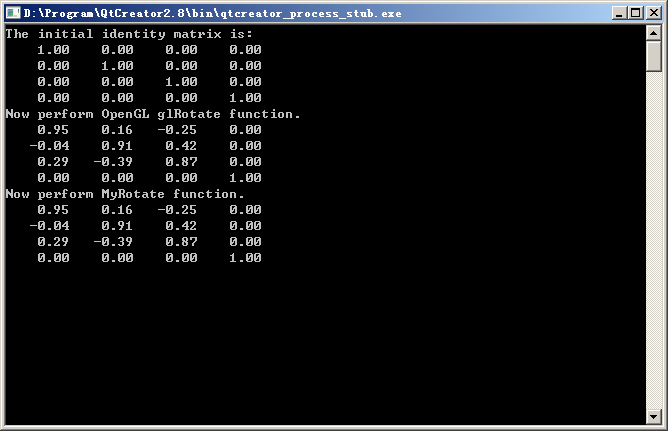
这说明上面的这条公式是正确的。如此一来我们就知道了glRotatef()的原理啦。其实D3DXMatrixRotationAxis()函数也是这样操作的,只不过D3D是左手坐标系,它的矩阵构建方法又会有所不同。