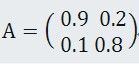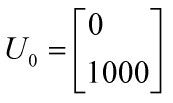谷歌网页排序背后的通信原理

注：更新于2015/08/02，增加了博文打赏，见文章结束后的二维码。如果您觉得此博文帮助了您，愿意打赏，请您阅读博文一个艰难的决定 ，了解为何添加博文打赏。

真的是很久没有写新文章了，上个月获得了一个CSDN颁发的“恒”字奖章，感觉是另一种幸福与满足，至少肯定了我一个月来的尝试。

今天为什么选择这样一个文章标题，其中有几点原因：

1）最近看果壳网上的死理性派文章，里面有许多有趣的科普文章，今早看见了一篇《谷歌怎样给网页排序》的文章，作者sqybi写的很好，喜欢这样的文笔，本文很多模型借源于此篇博文，可以说这篇文章给了我动机，自己只是站在巨人的肩膀上，把他没有证明的问题用一种方式给实现了，可能是sqybi觉得太简单没必要吧。

2）另一个原因，既然自己以后献身通信了，现在貌似通信领域大家普遍觉得遇到了瓶颈。但是，我想说的是，其实通信的基本原理包括概率论等知识，其实会永远熠熠生辉的，就像Gallager教授说的那样，Communication is not dead!,他写了一本《Principles of Communication》，来阐述那些复杂现象后的基本原理，中文版是母校北邮杨鸿文老师翻译，觉得是非常不错的一本书。

3）最后，这篇文章背后的原理，其实我很早之前有过强烈的动机来阐述，记得当时是看线性代数的时候，但是，惰性使然，没能及时写下来。这也让我明白一个道理，只有当知识和实际东西联系在一起后，我自己才有动力，可是，为什么，自己没有能力主动把学过的知识运用到实际中去呢？这就是差距吧。

注：为了尊重原著，红色部分的都是     引用自sqybi文章，其余才是自己写的。

Sqybi文章链接：谷歌怎样给搜索结果排序

 

好了，开始今天的话题吧，我们知道最传统的网页搜索结果排序是基于访问量的，但是这种排名算法有两个很显著的问题：一是因为只能够抽样统计，所以统计数据不一定准确，而且访问量的波动会比较大，想要得到准确的统计需要大量的时间和人力，还只能维持很短的有效时间；二是访问量并不一定能体现网页的“重要程度”——可能一些比较早接触互联网的网民还记得，那时有很多人推出了专门“刷访问量”的服务。有没有更好的方法，不统计访问量就能够为网页的重要度排序呢？

就是在这种情况下,1996 年初，谷歌公司的创始人，当时还是美国斯坦福大学研究生的佩奇和布林开始了对网页排序问题的研究。在1999年，一篇以佩奇为第一作者的论文发表了，论文中介绍了一种叫做 PageRank 的算法，这种算法的主要思想是：越“重要”的网页，页面上的链接质量也越高，同时越容易被其它“重要”的网页链接。于是，算法完全利用网页之间互相链接的关系来计算网页的重要程度，将网页排序彻底变成一个数学问题，终于摆脱了访问量统计的框框。

下面，我们利用sqybi文章中一个很好的例子来阐述这个问题

 

在详细讲述这个算法之前，不妨让我们用一个游戏，先来简单模拟一下 PageRank 算法的运行过程，以便读者更好地理解。

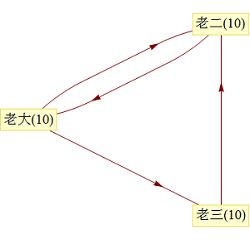
三兄弟分 30 颗豌豆。起初每人 10 颗，他们每次都要把手里的豌豆全部平均分给自己喜欢的人。下图表示了三兄弟各自拥有的初始豌豆数量，以及相互喜欢的关系（箭头方向表示喜欢，例如老二喜欢老大，老大喜欢老二和老三）。

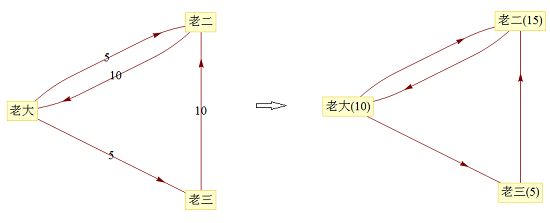
第一次分配后，我们会得到结果如下：

就这样，让游戏一直进行下去。直到他们手中的豌豆数不再变化为止。

在这里，我们把 “链接”比作“喜欢”，我们的模型是刚开始 每个人（好比网页）权重（网页重要级）是10，老大链接了老三，同时也链接了老二；老二只链接了老大，老三只链接了老二。

那么这个游戏到底是否可以结束呢，如果可以，最终的结果又是什么样的？在此我们用电脑模拟了这个过程，得出的结果是：老大和老二的盘子里各有 12 颗豌豆，而老三的盘子里有 6 颗豌豆。这时候无论游戏怎么进行下去，盘子里的豌豆数量都不会再变化。

好了，我们的任务就是用通信里的基本原理来解释这个迭代过程，高中的数列就是基本的迭代，一阶，二阶，或者是三阶，例如斐波拉契数列Fn+1 = Fn + Fn-1,利用通信里的术语就是二阶差分方程，记得高中的解法是直接把方程用二元函数表示为X^2-X-1=0,可以求解出两个特征根，非常熟悉的两个数字1.618和-0.618，然后利用这两个数构造等比数列最后求解出数列的表达式。当时我不知道为什么这样做就可以，反正这种差分的当时就直接那样上手了，很暴力有点。

我们先回避下上述问题，先讲下今天的主题-----马尔科夫链，在通信里我们经常用到的模型，简单的说就是记忆长度为一，当前状态只受前一状态的影响，跟再前面发生的事情无关，用数学表达式表示如下：

我们会用在信道建模还有维特比译码环节中，可以说马尔科夫链串连了通信。

我们最关心的是什么？是一阶转移概率矩阵。我们先举出一个简单的例子来看看（随便一本信息论教材都会有），此例来自于MIT的教材：

Problem:现在有两地域，加州和麻省，每年末加州有百分之90的人继续选择住在加州，另外百分之10 的人则搬家至麻省；同样，麻省百分之80人口选择继续，其它选择搬家至加州。起始人口分布是 加州0人，麻省1000人，问经过若干年后，人口分布能否平衡，且最后的分布情况。

Solution:我们先把这个问题用前面所述的马尔科夫一阶状态转移矩阵表示如下：

矩阵含义解释如下：A(1,1)表示的是加州留下概率，A(2,1)表示加州搬家概率,A(:,1)也就A第一列表示加州人的选择情况，这种情况就好比发送"0"接受到是“0”或者是“1”概率一样的简单（有点类似离散信道模型），我们用一个列向量来表示两地方人口数：

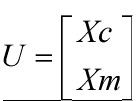 其中Xc表示加州人口数，Xm表示麻省人口数。可以是归一化的，也可以是具体数。

迭代方程如下：表示经过k年后两地人口数且初始状态为。

好了，我们问题的关键是怎么解决这样的迭代方程，我们不再像高中那样不知所措了，我们今天的主题就是线性代数，记得线性代数的核心就是特征值和特征向量，记得导师问过自己这样的问题，当时就蒙掉了。我们今天研究的矩阵很特别，它是马尔科夫矩阵，它有一些特征可以被我们利用，我们注意到马尔科夫矩阵所有列的和为1，那么它一定有一个特征值为1（证明见后记），既然有1就有稳态，另外其他特征值的绝对值都小于1。

让我们回顾下特征值和特征向量（我们前提是所有特征值不相同，那么根据线性代数矩阵就有n个线性无关特征向量）：

1）我们把U0用特征向量表示，意思是U0是n个特征向量的线性组合，即U0 = c1*x1+c2*x2+..+cn*xn;其中xn是线性无关的特征向量

2) 那么Uk怎么表示呢？A的k次幂去乘以U0得到什么呢？我们知道，特征向量的性质是,我们就有,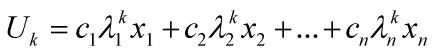,现在问题似乎明朗了点，我们假设为1，x1是lamda1对应的特征向量，其他特征值的绝对值都小于1，经过若干年后，除了第一项还存在外，其他都趋于0，那么意思是我们只要求出了x1的值就知道最后稳定的人口比例了。

3）我们直接用Matlab来求解吧，在Matlab里用[v d] = eig(A)可以求出特征向量和特征值，计算结果如下：

从图中可以看出对于特征值为1那个特征向量为[0.8944;0.4472]归一化后为[2/3:1/3]。终于我们找到了结果，意思是不管你起始分布怎么样，加州最后占总人口66.7%而麻省则占33.3%,这就是最后的稳态分布。转移矩阵A不变，那么特征向量不变，那么比例分布就不变，跟初始分布无关，常数C1不影响比例分布。其实在信息论里我们是这么求解的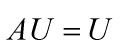，U就是马尔科夫链的平稳分布，我们解这个方程的过程其实是什么呢？其它就是在求特征值为1对应的那个特征向量啊！！我们把方程化简一下我们发现这不是求矩阵特征向量的方程嘛，对应的U就是A-I的零空间里的向量啊，我们减去了一个I，不就是求特征值为1对应的特征向量嘛，所以这里的U不就是那个向量V(:,1)=[0.8944:0.4472]嘛。其实我也是写到这才明白这么一个显而易见的道理，好吧！

 

现在终于可以回归到正题上了，我们要解决网页链接的问题，sqybi直接给出的结果是老大和老二的盘子里各有 12 颗豌豆，而老三的盘子里有 6 颗豌豆。这时候无论游戏怎么进行下去，盘子里的豌豆数量都不会再变化。我们希望用上面刚讲述的方法来验证一下：

1）写出状态转移矩阵

2）求特征值和特征向量：

我们发现同样有一个特征值为1，其他绝对值小于1

3）与特征值为1对应的特征向量是V(:,1) = [0.6667;0.6667;0.3333]归一化后为[0.4;0.4;0.2]

4）结果出来了，老大占0.4，老二占0.4，老三占0.1，由于总共有30颗，所以0.4*30 = 12 同样0.2*30 = 6。结果验证成功！

 

不同于之前的访问量统计，PageRank 求解了这样一个问题：一个人在网络上浏览网页，每看过一个网页之后就会随机点击网页上的链接访问新的网页。如果当前这个人浏览的网页 x 已经确定，那么网页 x 上每个链接被点击的概率也是确定的，可以用向量 Nx 表示。在这种条件下，这个人点击了无限多次链接后，恰好停留在每个网页上的概率分别是多少？

在这个模型中，我们用向量 Ri 来表示点击了 i 次链接之后可能停留在每个网页上的概率（ R ₀ 则为一开始就打开了每个网页的概率，后面我们将证明 R ₀ 的取值对最终结果没有影响）。很显然 R _i 的 L1 范式为 1 ，这也是 PageRank 算法本身的要求。

所以，通俗的说，就是刚开始我给每个网站的级别是一样的（假设），一般好的网站会有更多网站链接它，还有个事实是，一旦你被一个好的网站链接了，你的级别瞬间也就高了，这就是相辅相成吧。就如图中所示，我们可以预见，老二这个网站有两个网站链接它了，所以它是一个优秀的网站，虽然老大只有一个网站链接它，但这个网站就是优秀的老二，所以他的级别瞬间就跟同样只有一个链接的老三不一样了。

后记：

   1）最初的引题斐波拉契数列，我们同样可以用特征值来预测，但是我们这里有个littel trick，就是二阶变成一阶，怎么变换呢？我们的目标还是

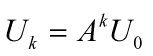我们的关键就是选择U和A了，这里我们选择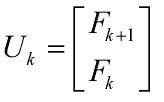和 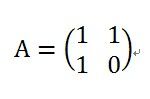就可以把菲波拉契数列变成我们熟悉的形式了，同样我们求解A的特征值，我们发现特征值就是1.618和-0.618，这就是为什么高中老师把这两个数叫做特征值的缘由吧。

    2）为什么马尔科夫矩阵肯定有一个特征值为1呢？我们发现如果某个矩阵有特征值为1，那么矩阵减去一个单位矩阵后，必须是奇异的，也就是行列式等于0，也就是存在行相关情况，当我们把马尔科夫矩阵对角线上元素减去1后，会发生什么呢？这个平移了单位矩阵的新矩阵是不是奇异的呢？必须是，肯定是！！原因是：原来马尔科夫每列的和是1，现在你每列减去了个1，那么现在每列的和肯定为0，好了，既然列和为0，那么行就是线性相关的了，那么就肯定是奇异的了。

 

总结：今天写这个文章，主要是把学到的东西来验证一些结果，作为sqybi文章的补充证明，那篇文章主要是科普，而我主要讲清楚一种计算机电脑模拟了这个过程是怎么实现的，以及它背后的通信原理的基本知识。

我的支付宝