社会化推荐算法

社会化推荐

本文是论文《一种结合推荐对象间关联关系的社会化推荐算法》（以下简称论文）的笔记（下）。该论文提出的算法是以PMF为框架基础的。因而若对PMF不太了解的话，可以参考我的上一篇文章脑补一下，当然，那篇文章只是概述，详细了解PMF还需要阅读初始论文，但读完那篇文章后，对本文的理解应该没有问题。

下载资源，猛击此处。

所谓社会化推荐算法，是将社交网络的特性加入到推荐系统中来。因为社交网络方兴未艾，因而这种算法也是当前的研究热点之一。主要的做法是利用用户间的社会关系，认为在社交网络中相互信任的朋友具有更大的相似度。论文的创意则是利用对象间关联关系来对推荐结果进行优化；举个例子说明它的合理性，用户买过羽毛球拍后，很可能会买羽毛球，羽毛球和羽毛球拍两个对象就有一定的关联。

先谈利用用户间相互关系的社会化推荐，一种具体做法是在社交网络中计算信任关系矩阵，信任关系具有两大特性：可以传播和可以预测；然后用信任矩阵代替推荐系统中的相似矩阵进行推荐。信任关系的计算在论文的参考文献9-10，但我猜测应该会考虑用户之间的交互强度、内容相似度、情景相似度等因素，可以参考我之前的文章《微博背后的那些算法》。在信任矩阵的计算上，论文中还提到其他算法如基于朋友圈的算法、考虑用户本身特征的算法等，有兴趣可以阅读原文。

另一种可能的方法是利用矩阵分解的手段，推荐系统与社交网络共享同一个用户隐式空间，用户隐式空间就是一个矩阵，矩阵由很多向量组成，每个向量都是用户的隐式特征向量。通过这样的手段，就将用户的社交网络关系同评分矩阵联系到一起了，这种算法称作SoRec算法。

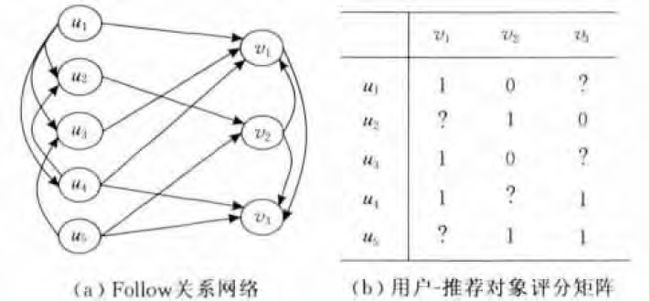
考虑一个具体的问题，即微博上的好友推荐问题。如图1所示：

图1 微博好友推荐问题

U是用户，V代表被推荐的对象。U之间的箭头表明用户之间的关注关系。V之间的箭头表示被推荐对象之间的关注关系。评分矩阵就是指U是否对被推荐用户满意，也即评分矩阵。

SoRec算法就是考虑了U之间关注关系的推荐方法。

在上一篇文章中的PMF介绍中，我们将评分矩阵R分解为用户隐式空间U和物品隐式空间V。在SoRec中，还有一个用户之间的信任关系矩阵D，我们将其分解为U和Q两个隐式空间，其中R分解后的U和D分解后的U是共享的。在PMF框架下，D分解为U和Q时也假设U、Q的隐式向量都服从高斯先验，U、Q推出D的条件概率也服从高斯先验。

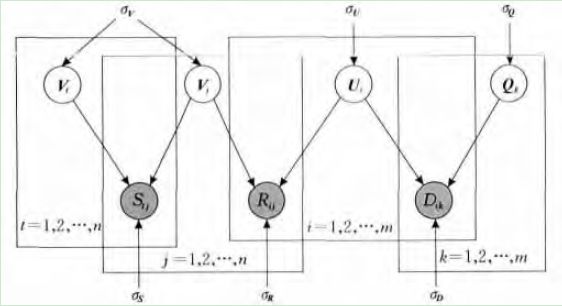
SoRec的概率图可以表示如图2所示。

由图2可知，SoRec算法其实就是使用用户的信任矩阵在用户隐式空间中添加了一层约束，从而达到使用用户的朋友的信息进行推荐的效果。

图 2 SoRec的概率图表示

由图1可知，有时候不仅仅是用户之间有关系，被推荐物品之间也可能会有关联。论文中提到了使用PropFlow的方法对被推荐物品进行关系计算，PropFlow使用对象间信息流的大小来衡量关系，信息流越大，关系越紧密。

依SoRec那样如法炮制，将物品的的关系矩阵S分解为物品隐式空间Vi和Vt的乘积。仍然套用PMF框架，做高斯先验假设。其概率图如图3所示。

图3 结合物品关系的社会化推荐概率图表示

这里让我很不解的是，为什么SoRec中用户关系矩阵D分解为U和Q时U和Q分别使用不同的高斯先验方差参数，而物品关系矩阵S分解为Vi和Vt时却只用一个参数？作为一个疑点，先保留下来吧，希望以后能搞明白。

在PMF框架下，其推导一般是将后验概率先取对数然后使用SGD算法等进行求导。具体的公式推算见原论文，本文只做科普用吧。本人也是第一次接触PMF，如果文章中有疏漏或偏差之处，还请各位读者多多指正。

图片有些模糊，但来源于原论文，需要的话也请去原论文中查看。